2 蚁群算法
2 蚁群算法
2.1 概述
蚁群算法和PSO同属于群体智能算法,利用群体的力量来尽可能找到问题的最优解。蚁群算法的原理是模拟现实生活中蚂蚁的觅食行为,蚂蚁在运动过程中会其经过的路径上留下信息素,而且蚂蚁也能够感知信息素的存在浓度,以此来指导自己的移动方向,每只蚂蚁都倾向于朝着信息素浓度高的方向移动。这就形成了正反馈现象,久而久之,几乎所有的蚂蚁都将选择同一条路径移动(因为这条路径的信息素浓度远远大于其他路径上的信息素)。
通过蚂蚁觅食的简单例子来说明蚁群算法的原理:
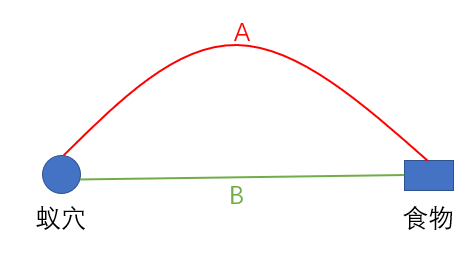
为了简化讨论,这里给出几个假设:
- 每只蚂蚁在行走过程中,会将信息素均匀释放到其行走的路径上。
- 每只蚂蚁从蚁穴到达食物处之后,将会马上原路返回。
- 每只蚂蚁运动速度都是恒定且相同的,并且路径A和路径B的长度关系为:\(L_A=2L_B\)。
因为刚开始的时候,路径A、B上均没有信息素,没有任何可以参考的信息,因此对于蚂蚁来说只需要随机选择一条路径即可,于是路径A和路径B被选中的概率都是50%。为了简化讨论,我们可以认为有刚开始只有一只蚂蚁选择了路径A,一只蚂蚁选择了路径B。
由于路径B比较短,当路径B上的蚂蚁原路返回到蚁穴的时候,选择路径A的蚂蚁才刚到食物处。这就造成了此时路径B上的信息素浓度会是路径A上浓度的2倍。如果后续还有蚂蚁去寻找食物,那么它们将更加倾向于选择路径B,这就形成了正反馈效果。最终,几乎所有的蚂蚁将选择路径B。
通过上述这个简单的例子,我们知道蚂蚁就是利用了更短的路径将会聚集更多的信息素这一点,来指导自己选择路径。基于这个原理,我们可以将蚁群算法应用于寻找最短路径的问题当中。
2.2 基本蚁群算法
这里以解决TSP(旅行商问题)为例,来阐述具体的蚁群算法。
TSP问题实际上就是一个最小路径问题,假设一共有N个城市(分别标记为\(1,2,\cdots,n\)),不同城市之间的距离用一个矩阵\([d_{ij}]_{n\times n}\)来表示,其中\(d_{ij}\)表示城市\(i\)到城市\(j\)的距离,如果这两个城市不可达可以将该距离标记为无穷大。那么我们的目标就是找到一条路径不重复地连接所有城市并使路径长度尽可能小。
蚁群算法对TSP的求解具有两大步骤:路径创建,信息素更新。
路径创建: 算法刚开始,每只蚂蚁随机选定一个城市作为出发地,然后不重复地遍历所有城市。在这过程中每只蚂蚁需要记住它自己行走过的路径,还要记住它所走过的长度(用于更新信息素,以及判断解的优劣)。在选择下一个城市的时候,需要根据一定的规则进行随机选择,规则如下:
- 其中\(P_{ij}^{(k)}\)表示第\(k\)只蚂蚁从城市\(i\)到达城市\(j\)的概率,这意味着当前蚂蚁位于第\(i\)个城市。
- \(allowed_k\)表示第\(k\)只蚂蚁尚未访问过的城市集合。
- \(\eta_{ij}=1/d_{ij}\)表示路径\(ij\)的能见度
- \(\tau_{ij}\)表示路径\(ij\)上的信息素浓度
- \(\alpha,\beta\)两个实现设定好的参数,分别用于信息素和能见度的加权
信息素更新: 首先,我们需要初始化信息素浓度,如果初始值选得太小,算法容易早熟,蚂蚁会很快集中到局部最优路径上。如果选得太大,信息素对搜索方向的指导作用就太低,也会影响算法性能。通常,我们可以借助贪心算法来初始化,即
其中\(m\)是蚁群规模(蚂蚁个数),\(C_{nn}\)是通过贪心算法找到的路径长度。
每条路径上的信息素更新公式如下:
这里我们用\(t\)表示迭代的次数;\(\rho\)表示信息素的蒸发率;\(\Delta\tau_{ij}^{(k)}(t)\)表示第\(k\)只蚂蚁在路径\(ij\)上所贡献的信息素浓度,具体定义如下:
其中\(C_k\)表示第\(k\)只蚂蚁走完整条路经后所得到的总路径长度。实际上这相当于每只蚂蚁将1单位的信息素均匀撒在它所经过的路径上。
从信息素的更新可以看出,影响信息素更新的两大因素是:信息素蒸发、信息素增强。
信息素蒸发可以避免算法过快地收敛到局部最优解当中,有助于搜索区域的扩展。
信息素增强实际上有两种主要的更新方式离线更新与在线更新。离线更新指的是当蚁群中的所有蚂蚁全部完成对所有城市的访问后,统一对信息素进行更新。而在线更新是蚂蚁每走一步就进行信息素更新。在这里我们采用离线更新的方式。
算法流程
- 初始化种群大小\(m\)等必要的参数,以及算法终止条件;
- 使用贪心算法初始化每条路径上的信息素浓度;
- 随机初始化\(m\)只蚂蚁,当蚁群中的所有蚂蚁全部完成对所有城市的访问后,统一对信息素进行更新;这一步需要反复多次执行。
- 当算法满足终止条件,输出找到的最优解。
2.3 代码实现与测试
这里测试了4个城市的对称TSP问题,代码如下:
import numpy as np
class Ant:
def __init__(self, n):
# 城市数目
self.n = n
def init(self):
# 未访问过的城市:0,1,2, ..., n-1
self.allowed = [i for i in range(self.n)]
# 随机初始化蚂蚁的初始城市
city = np.random.randint(self.n)
self.path = [city]
self.allowed.remove(city)
# 路径长度
self.distance = 0
# 信息素更新矩阵 pher[i,j]==1表示蚂蚁经过了i->j这条路径
self.pher = np.zeros((self.n, self.n))
def get_pheromone(self, Q):
# 每只蚂蚁携带Q个单位的信息素
return Q / self.distance * self.pher
def get_path(self):
return self.path, self.distance
def travel(self, D, P, alpha, beta):
while self.allowed:
# 计算访问下一个城市的概率
prob = []
for city in self.allowed:
d = D[self.path[-1], city]
pher = P[self.path[-1], city]
prob.append(
((1 / d) ** alpha) * (pher ** beta)
)
# 归一化
prob = np.array(prob) / sum(prob)
# 选择下一个城市
next_city = np.random.choice(self.allowed, p=prob)
self.distance += D[self.path[-1], next_city]
# 如果i->j和j->i的距离是不对称的,那么更新方式为:self.pher[self.path[-1], next_city] = 1.0
self.pher[[self.path[-1], next_city], [next_city, self.path[-1]]] = 1.0
self.path.append(next_city)
self.allowed.remove(next_city)
# 回到起点
self.distance += D[self.path[-1], self.path[0]]
self.path.append(self.path[0])
# 如果i->j和j->i的距离是不对称的,那么更新方式为:self.pher[self.path[-1], self.path[0]] = 1.0
self.pher[[self.path[-1], self.path[0]], [self.path[0], self.path[-1]]] = 1.0
class TSP:
def __init__(self, m, n, D, P, Q, alpha, beta, rho, num_iter):
# 蚂蚁个数
self.m = m
# 城市个数
self.n = n
# 距离矩阵
self.D = D
# 信息素矩阵
self.P = P
# 当前最佳路径
self.path = None
self.distance = np.inf
# 每只蚂蚁携带的信息素
self.Q = Q
self.alpha = alpha
self.beta = beta
# 信息素蒸发系数
self.rho = rho
# 迭代次数
self.num_iter = num_iter
# 蚂蚁种群
self.ants = [Ant(n) for _ in range(m)]
def solve(self):
for _ in range(self.num_iter):
phers = np.zeros((self.n, self.n))
for ant in self.ants:
ant.init()
for ant in self.ants:
ant.travel(self.D, self.P, self.alpha, self.beta)
phers += ant.get_pheromone(self.Q)
path, dist = ant.get_path()
if dist < self.distance:
self.path = path
self.distance = dist
# 跟新信息素
self.P = (1 - self.rho) * self.P + phers
return self.path, self.distance
if __name__ == '__main__':
# 4个城市对称TSP问题
D = np.array([
[0, 11, 2, 1],
[11, 0, 1, 2],
[2, 1, 0, 1],
[1, 2, 1, 0],
])
# 为了简单起见,路径上的信息素初始化为0
P = np.ones((4, 4))
tsp = TSP(
m=5,
n=4,
D=D,
P=P,
Q=1,
alpha=0.5,
beta=0.5,
rho=0.5,
num_iter=5
)
path, length = tsp.solve()
print(path, length)
测试结果:

2.4 蚁群算法的变种
在基本的蚁群算法之上,演化出了各种改进版本的蚁群算法,这些算法仅在搜索控制策略方面有所差异。
精英蚂蚁系统(Elitist Ant System,EAS)
使用精英策略指的是对于已发现的最好路径给予额外的增强,假设在算法搜索过程中,所找到的历史最优路径为\(T_{best}\),经过历史最优路径的蚂蚁称为精英。当信息素进行更新的时候,将会对最佳路径\(T_{best}\)进行额外的增强,使得选择该路径的概率更大,从而增大较好路径的选择机会。
信息素更新公式为:
其中
\(e\)是增强系数,\(C_{best}\)则是历史最优路径的长度。
这种改进能够以更快的速度获得较好的解,但是这也可能较早收敛到局部次优解,从而导致搜索过程过早的停滞。
基于排列的蚁群系统(Rank-based Ant System)
基于排列的蚁群系统则是对精英蚂蚁策略的进一步改进,该算法不仅对最佳路径的信息素有所增强,同时也对其余各边的信息素更新机制进行了一定的改善。
更新公式为:
当全部的\(m\)只蚂蚁完成对所有城市的访问之后,需要对这些蚂蚁进行重新排列,所经过路程越短的,排在越前面,即\(C_1\le C_2\le\cdots\le C_m\)。
可以看到除了保留精英策略之外,同样对第\(t\)次迭代中其他蚂蚁释放的信息素进行加权求和。
其他的变种还有最大最小蚂蚁系统(MAX-MIN Ant System, MMAS)、蚁群系统(Ant Colony System, ACS)等。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号