感知机模型
感知机模型
简单来说,感知机模型就是一个针对线性可分问题的二分类器。假设有线性可分数据集\(D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\cdots,(\mathbf{x}_m,y_m)\}\),其中\(\mathbf{x}\in\mathbb{R}^n\)是样本的特征向量,\(y\in\{-1,1\}\)是样本的标签。感知机模型通过一个线性变换与符号函数(sign)将样本特征映射成样本标签,具体数学公式如下:
其中\(\mathbf{w}\in\mathbb{R}^n\)是感知机的权重,\(b\in\mathbb{R}\)是感知机的偏置参数。
那么,如何理解感知机模型呢?为了方便讨论,我们将\(\mathbb{R}^n\)空间中的超平面方程改写为\(\mathbf{w}^{\rm T}\mathbf{x}=b\),这个超平面将整个\(\mathbb{R}^n\)空间切分为两个部分(即两个半空间)。
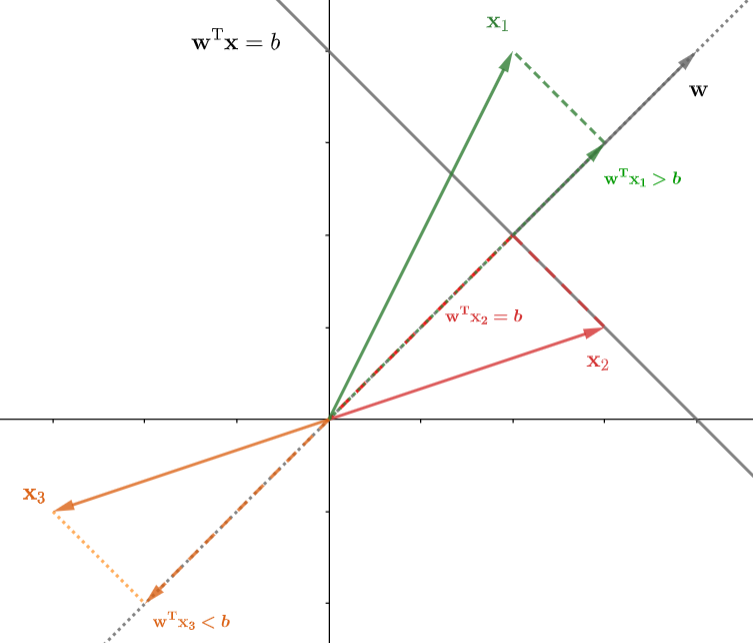
如上图所示,在超平面上的点\(\mathbf{x}_2\)(红色),在超平面法向量\(\mathbf{w}\)方向上的投影为\(\mathbf{w}^{\rm T}\mathbf{x}_2=b\);在法向量方向一侧的点\(\mathbf{x}_1\)(绿色),在法向量方向的投影\(\mathbf{w}^{\rm T}\mathbf{x}_1>b\);在法向量另一侧的点\(\mathbf{x}_3\)(橙色),在法向量方向上的投影\(\mathbf{w}^{\rm T}\mathbf{x}_3<b\)。
从图可以直观的看出,如果样本点在法向量正方向的一侧,那么\(\mathbf{w}^{\rm T}\mathbf{x}-b>0\);如果样本点在法向量负方向的一侧,那么\(\mathbf{w}^{\rm T}\mathbf{x}-b<0\)。为了直接输出样本标签,就可以利用符号函数直接输出\(\{-1,+1\}\)。
感知机的训练策略
为了后面叙述方便,这里先引入两个小知识点:函数间隔、几何间隔。样本点\(\mathbf{x}\)到超平面的距离公式为
如果将分子上的绝对值去掉,并引入样本标签(\(y\in\{-1,1\}\)),即可得到几何间隔:\(y(\mathbf{w}^{\rm T}\mathbf{x}+b)/||\mathbf{w}||\)。几何间隔实际上就是带符号的距离,几何间隔的绝对值就是点到超平面的距离。如果几何间隔为正,表示该样本点被正确分类。如果几何间隔为负,表示该样本被错误分类。
将几何间隔的分母去掉,即可得到函数间隔:\(y(\mathbf{w}^{\rm T}\mathbf{x}+b)\)。函数间隔保留了几何间隔的符号,函数间隔的绝对值大小也一定程度上反映了样本点到超平面的距离大小。但需要注意的是,如果要通过函数间隔的绝对值比较来确定哪一个样本距离超平面更远,需要保证在比较的时候,所使用的\(\{\mathbf{w},b\}\)必须相同。这是因为,只要同时缩放\(\{\mathbf{w},b\}\)就能改变函数间隔的值,并保持超平面不变。也就是说,对于任意的\(\lambda\ne0\),\(\lambda(\mathbf{w}^{\rm T}\mathbf{x}+b)=0\)所表示的超平面本质上都是同一个。
感知机训练的最终目标就是确定参数\(\{\mathbf{w},b\}\),将数据集中的线性可分数据通过一个超平面分开。为此,需要确定一个损失函数。一个简单的想法便是使用点到超平面的距离来度量损失,对于误分类的样本来说,如果该样本距离超平面的距离越远,损失值就越大。此外,我们不去考虑已分类正确的样本,即已正确的样本对应的损失值为0。那么,可以容易写出数据集上误分类样本的总体损失:
其中,对于误分类样本而言,\(y_i(\mathbf{w}^{\rm T}\mathbf{x}_i+b)\le0\)。因为\(1/||\mathbf{w}||\)的存在,直接优化上述式子存在一定的困难。如果直接忽略该项,那么可以得到感知机的最终损失函数:
直接忽略\(1/||\mathbf{w}||\),相当于使用误分类样本的函数间隔绝对值作为损失值,而不是使用几何间隔绝对值。
对损失函数求导即可得到:
在实际训练的时候,通常是逐个样本进行训练,直到训练集中的所有样本都被正确分类。具体的训练算法描述如下:
-
随机初始化感知机参数:\(\{\mathbf{w},b\}\)
-
选择样本\((\mathbf{x}_i,y_i)\in D\)
-
如果\(y_i(\mathbf{w}^{\rm T}\mathbf{x}_i+b)\le0\),那么通过梯度下降法更新参数:
\[\mathbf{w}\leftarrow\mathbf{w}+\gamma y_i\mathbf{x}_i\\ b\leftarrow b +\gamma y_i \] -
不断重复1,2步,直到训练集\(D\)中的所有样本都被正确分类。
其中\(\gamma\in(0,1)\)是学习率。
为了更好理解上述更新过程,可以计算函数间隔\(y_i(\mathbf{w}^{\rm T}\mathbf{x}_i+b)\)更新后的变化:
可以看到右侧第一项是更新前的函数间隔,右侧第二项\(\gamma(\mathbf{x}_i^{\rm T}\mathbf{x}_i+1)>0\)。因此,更新后的参数使得当前误分类样本的函数间隔增加。
从几何的角度来看的话,参数的更新过程就是使超平面向误分类样本靠近的过程,直到样本被正确分类。
感知机的对偶形式
通过上述感知机的训练算法可知,每次更新参数,就是不断在\(\mathbf{w}\)上累加\(\gamma y_i\mathbf{x}_i\),在\(b\)上累加\(\gamma y_i\)。假设,在感知机训练至收敛的过程中样本\(\mathbf{x}_i\)被分错的次数记为\(m_i\),初始参数为\(\mathbf{w}_0\),那么最终训练得到的参数为
为了简单起见,可以将初始值\(\{\mathbf{w}_0,b_0\}\)都置为0,并且令\(\alpha_i=m_i\gamma\)。于是,最终训练得到的感知机模型可以写为
于是,感知机训练算法可以重新叙述为:
-
初始化感知机参数:\(\alpha_i=0(1\le i\le m),b=0\)
-
选择样本\((\mathbf{x}_j,y_j)\in D\)
-
如果\(y_j\left(\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i^{\rm T}\mathbf{x}_j+b\right)\le0\),那么更新参数:
\[\alpha_j\leftarrow\alpha_j+\gamma\\ b\leftarrow b +\gamma y_j \] -
不断重复1,2步,直到训练集\(D\)中的所有样本都被正确分类。
可以发现在对偶形式的感知机模型中,训练样本总是以内积的形式出现,因此,在训练模型之前,可以事先将样本两两组合计算内积,并将计算结果存储起来,后续训练过程中直接查询结果即可。可以将样本向量组织成矩阵的形式,然后进行计算
其中\(\mathbf{X}\)的第\(i\)列表示样本\(\mathbf{x}_i\);\(\mathbf{G}\)被称为Gram矩阵,该矩阵中的每个元素表示一对向量的内积,即\(\mathbf{G}_{ij}=\mathbf{x}_i^{\rm T}\mathbf{x}_j\)。
感知机的其它一些问题
感知机的收敛问题:
- 对于线性可分数据集,感知机模型经过有限次更新后,一定能够收敛。具体的证明过程可以参照《统计学习方法》第二版中的Novikoff定理。
- 感知机最终收敛的参数与参数的初始值和样本训练的顺序相关。不同的样本训练次序,不同的初始值都会影响感知机模型最终收敛的参数。
- 如果数据集线性不可分,感知机的训练过程将发生震荡,无法收敛。
与逻辑回归的差别:
- 感知机是判别模型,通过符号函数\(\text{sign}(\cdot)\)直接输出样本标签\(y\),逻辑回归则是通过\(\text{sigmoid}\)输出条件概率值\(p(y|\mathbf{x})\)。因此,逻辑回归可以通过概率值的大小表示分类的可靠程度。
- 在训练过程中,符号函数是不可导的,需要另外寻求替代的损失函数。逻辑回归则可以直接使用交叉熵作为损失函数。
与支持向量机的关系:
- 如果一个数据集是线性可分的,那么就存在无穷多个超平面将该数据集切分为两部分。那么如何从中选择一个超平面呢?感知机对超平面的选择完全依赖于初始值的设置,以及样本的训练次序。支持向量机则是选择能够将样本完全分离,且间隔最大化的超平面。


