2020杭电多校第四场 Go Running 最小点覆盖等于二分图最大匹配数

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6808

思路：刚开始也是乱想，想几下就忍不住画个t-x图像，然后每个点有两种可能，一是向西跑，一是向东跑。在图中都画出来发现：

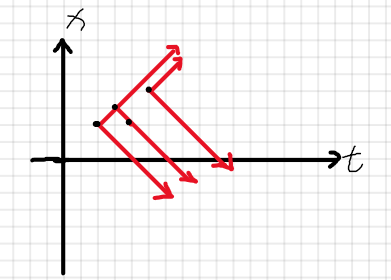我画了4个点，箭头表示可能移动的方向，这时候发现这不就是找“覆盖所有点最少需要多少条直线”吗？我蠢的是刚开始就想到了这里，然后我忘了怎么找了，这种模板题当初学二分图时就做过，到了最后20分钟恍然大悟：把横纵坐标分别当做二分图的两边，把点所在的横纵坐标相连。因为我们把横纵坐标当做了二分图的点，二分图中的一个边就代表一个点。到这里就很清楚了，我们求的就是：选最少的点使得二分图中每条边都有端点被覆盖。最小点覆盖就是：选最少的点让二分图中每个边都有端点被选。最大匹配数 = 最小点覆盖。n = 1e5，肯定dinic，套个板子就行了。

咦？怎么知道点是不是在一条直线呢？直接旋转坐标系45度就行了。

x'=x·cos(θ)+y·sin(θ)

y'=y·cos(θ)-x·sin(θ)

我就直接用map哈希的，分配编号就行了。

 

 

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) ((-x)&x)
#define met(a, b) memset(a, b, sizeof(a))
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define bep(i, a, b) for(int i = a; i >= b; i--)
#define pb push_back
#define mp make_pair
#define debug cout << "KKK" << endl
#define ls num*2
#define rs num*2+1
#define re return
using namespace std;
const ll mod = 1e9 + 7;
const double PI = acos(-1);
const ll INF = 2e18+1;
const int inf = 1e9+5;
const double eps = 1e-10;
const int maxn = 2e5 + 5;
inline char gc(){
    static char buf[100000],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
#define gc getchar
inline int rd(){
    int x = 0; char ch = gc(); bool positive = 1;
    for (; !isdigit(ch); ch = gc())    if (ch == '-')     positive = 0;
    for (; isdigit(ch); ch = gc())    x = x * 10 + ch - '0';
    return positive ? x : -x;
}
map<double, int> vx, vy;

ll dis[maxn];
int tot=1, cur[maxn],ne[maxn]; // tot初始化为1哦。

struct node {
    int to,net;
    long long val;
} p[maxn*2];

inline void add(int u,int v,long long w) {
    p[++tot] = (node){v, ne[u], w};
    ne[u] = tot;
}

inline int bfs(int s, int t) { 
    for(register int i=1;i<=t;i++) dis[i]=inf;
    queue<int> q;
    q.push(s);
    dis[s]=0;
    cur[s]=ne[s];
    while(!q.empty()) {
        int x=q.front();
        q.pop();
        for(register int i=ne[x];i;i=p[i].net) {
            int v=p[i].to;
            if(p[i].val>0&&dis[v]==inf) {
                q.push(v);
                cur[v]=ne[v];
                dis[v]=dis[x]+1;
                if(v==t) return 1;
            }
        }
    }
    return 0;
}

inline ll dfs(int x,long long sum,int t) { 
    if(x==t) return sum;
    long long k,res=0; 
    for(register int i=cur[x];i&&sum;i=p[i].net) {
        cur[x]=i; 
        int v=p[i].to;
        if(p[i].val>0&&(dis[v]==dis[x]+1)) {
            k=dfs(v,min(sum,p[i].val), t);
            if(k==0) dis[v]=inf; 
            p[i].val-=k;
            p[i^1].val+=k;
            res+=k; 
            sum-=k;
        }
    }
    return res;
}

ll dinic(int s, int t){
    ll ans = 0;
    while(bfs(s, t)) {
        ans+=dfs(s,inf, t); 
    }
    return ans;
}


int main(){
    // ios::sync_with_stdio(false);
    // cin.tie(0); cout.tie(0);
    int T = rd();
    double xx, yy, sq = sqrt(2)/2; //sq就是sin(θ)
    int x, t, dx, dy;
    int n, m, px, py;
    while(T--){
        vx.clear(); vy.clear();
        n = rd(); tot = 1;
        px = 0, py = n;
        int st = 0,  en= 2*n + 3; // 源点汇点
        rep(i, 0, en) ne[i] = 0;
        rep(i, 1, n){
            x = rd();
            t = rd();
            xx = sq*(x + t);
            yy = sq*(x - t);  //旋转后的坐标
            if(!vx.count(xx)) vx[xx] = ++px;  
            if(!vy.count(yy)) vy[yy] = ++py; // 分派编号
            dx = vx[xx], dy = vy[yy];
            add(dx, dy, 1);
            add(dy, dx, 0); // 二分图建边
        }
        rep(i, 1, px){
            add(st, i, 1);  
            add(i, st, 0); //源点建边
        }
        rep(i, n+1, py){
            add(i, en, 1);
            add(en, i, 0); //汇点建边
        }
        cout << dinic(st, en) << endl;
    }
    return 0;
}