Gym 101490K Safe Racing (dp转换， 超超超级详细，包你看懂）

题意：给你一个长为L的圆形跑道，让你放置警示牌，相邻两个警示牌相隔距离不能超过S，让你求有多少种方案数放置。数据L，S都是1e6。

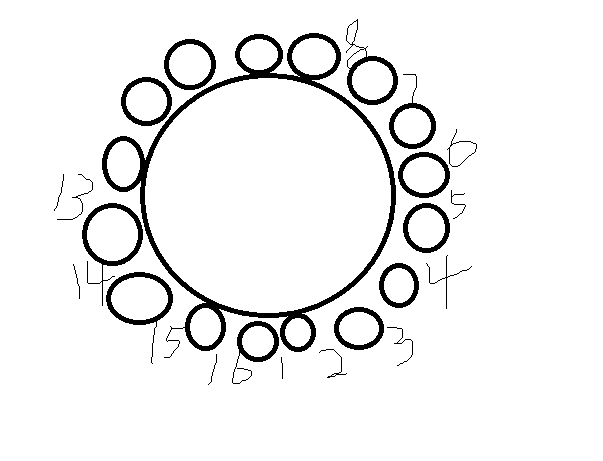
来个例子：L = 13， S = 5。一个圈表示长度为1。

思路：因为是一个圈，我们必须得判断最后一个牌子和第一个牌子的相距距离，所以如果我们规定了第一个放在那，最后一个放在那，这道题就简单多了。比如这个。

第一步思考：

1 当我们第一个放在1号位子时，我们最后一个能放的位置有12，13，14，15，16。

2 当我们第一个放在2号位子时，我们最后一个能放的位置有13，14，15，16。

3 当我们第一个放在3号位子时，我们最后一个能放的位置有14，15，16。

4 当我们第一个放在4号位子时，我们最后一个能放的位置有15，16。

5 当我们第一个放在5号位子时，我们最后一个能放的位置只有16。

6 当我们第一个放在6号位子时，不行，因为最大不能相差6，如果放在了6，我们得在1到5之间放置一个警示牌，和前面的情况已经重复了。

 

 

 

第二步思考：

确定了第一个位子和最后一个位子，你只需要确定中间能放置的种类不久行了吗？然后你想一会会发现这不就是求一个直行跑道放警示牌能放多少种吗？最多不能相隔s，你刚开始做dp时，每次上台阶你只能上1或者2阶，n阶的楼梯你可以走的方案数有多少种？这个题不就是你每次可以走1~S阶，求走n阶的方案数么?你的dp[i]表示的就是长度为i，在第i这个地方放置一个牌子的方案数。 所以dp[i]就等于dp[i-1]+dp[i-2]....+dp[i-s+1]啊。这不就写出来了吗？

需要注意的是，长度为三的，是有4个点，因为0可以放。

 

 

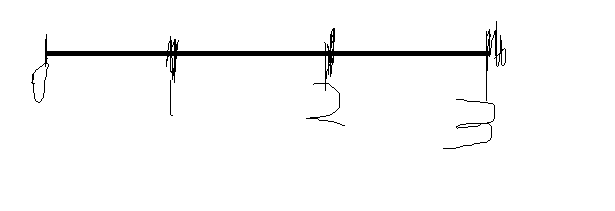
 正常写是这样

dp[0] = 1;
    for(int i = 1; i <= l; i++){
        for(int j = i-1; j >= max(0, i-s); j--){
            (dp[i] += dp[j]) %= mod;
        }
    }

但是复杂度肯定说不过去，再一想你想要的只不过要维护一个长为s的区间和而已，所以直接记录前s个的前缀和，然后每次加一个是，减去你维护的区间第一个值就行了。

    dp[0] = now = 1;
    for(int i = 1; i <= l; i++){
        dp[i] = now;
        (now += dp[i]) %= mod;
        if(i >= s){  //维护长度为s的区间和。
            now = (now - dp[i-s] + mod) % mod;
        }
    }

还记得第一步吗？

 

 

 我们要的答案就是这些的对应位置的dp值相加。

就变成了：

 

1 当我们第一个放在1号位子时，我们最后一个能放的方案数有dp[11] + dp[12] + dp[13] + dp[14] + dp[15]

2 当我们第一个放在2号位子时，我们最后一个能放的方案数有dp[11] + dp[12] + dp[13] + dp[14]

3 当我们第一个放在3号位子时，我们最后一个能放的方案数有dp[11] + dp[12] + dp[13] 

4 当我们第一个放在4号位子时，我们最后一个能放的方案数有dp[11] + dp[12]

5 当我们第一个放在5号位子时，我们最后一个能放的方案数有dp[11]

再开一个数组记录dp的前缀和就能直接算了。

这题就a了。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod = 123456789;
const int maxn = 1e6 + 5;
ll dp[maxn], sum[maxn];
int main(){
    ll l, s;
    cin >> l >> s;
    ll now = 1;
    dp[0] = 1;
    sum[0] = 1;
    for(int i = 1; i <= l; i++){
        dp[i] = now;
        sum[i] = (sum[i-1]+dp[i]) % mod; // 前缀和
        (now += dp[i]) %= mod;
        if(i >= s){
            now = (now - dp[i-s] + mod) % mod;
        }
    }
    ll ans = 0;
    for(int i = 1; i <= s; i++){
        ans = (ans + sum[l-i] - sum[l-s-1] + mod)%mod;
    }
    cout << ans << endl;
    return 0;
}