跟着xiaoxin巨巨做cf
题目大意：有一个数列{xi},每次给出一个询问[l, r]，即问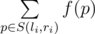
S(l ,r)是l和r之间的素数,ｆ(p)表示数列{xi}中整除ｐ的个数
思路:筛法，显然xi的顺序是无所谓的,我们把它记录下来，然后做筛法,如果一个素数筛合数的过程中遇到一个数的话显然得记到这个素数的头上,然后再把这样得到的表求一个sum就行
1 #include<iostream> 2 #include<cstdio> 3 #define maxn 10000009 4 int sum[maxn*5],ans[maxn*5]; 5 bool visit[maxn*5]; 6 int main() 7 { 8 int n,m,x,y; 9 scanf("%d",&n); 10 for(int i=1;i<=n;i++) 11 { 12 scanf("%d",&x); 13 sum[x]++; 14 } 15 for(int i=2;i<=maxn;i++) 16 { 17 if(!visit[i]) 18 { 19 for(int j=1;j*i<=maxn;j++) 20 { 21 visit[i*j]=1; 22 ans[i]+=sum[i*j]; 23 } 24 } 25 ans[i]+=ans[i-1]; 26 } 27 scanf("%d",&m); 28 for(int i=1;i<=m;i++) 29 { 30 scanf("%d%d",&x,&y); 31 if(x>=maxn )x=maxn; 32 if(y>maxn)y=maxn; 33 printf("%d\n",ans[y]-ans[x-1]); 34 } 35 36 return 0; 37 }
cf 14 E Camels
题目大意:问你长度为n的数列,其中只有1 到4 ,有t个峰 t-1个谷并且不存在连续两个相同高度的序列的个数
思路:dp[i][j][k][b]表示现在到第i个数字,第i个数字为j,有k个驼峰，如果第i个点高于第i-1个点那么b＝０,不然b＝１,可以很自然的推出转移，不过需要注意的是仔细画一下就可以发现峰和谷必然是交替出现的,并且在头和尾上必然是一个上升一个下降的,不然不可能满足t-1个谷,所以在i＝２的时候强制上升就可以了
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int dp[21][21][21][2]; 5 int main() 6 { 7 int n,t; 8 scanf("%d%d",&n,&t); 9 for(int i=1;i<=4;i++)dp[1][i][0][0]=1; 10 for(int i=2;i<=n;i++) 11 { 12 for(int j=1;j<=4;j++) 13 { 14 for(int k=0;k<=min(i,t);k++) 15 { 16 for(int m=1;m<=j-1;m++) 17 { 18 dp[i][j][k][0]+=dp[i-1][m][k][0]+dp[i-1][m][k][1]; 19 } 20 if(i!=2)for(int m=j+1;m<=4;m++) 21 { 22 dp[i][j][k][1]+=dp[i-1][m][k-1][0]+dp[i-1][m][k][1]; 23 } 24 } 25 } 26 } 27 int ans=0; 28 for(int i=1;i<=4;i++)ans+=dp[n][i][t][1]; 29 printf("%d\n",ans); 30 return 0; 31 }
cf 69D Dot
题目大意:一开始在坐标系中有一个点,两人轮流操作,每次操作可以将一个点走一个偏移量（偏移量是给定的,题目给出了一坨偏移量,每次选择一个）,或者每个选手有一次机会把点做y=x的对称操作,谁让点离远点欧几里的距离超过ｄ谁就输,问谁胜
思路:博弈dp，利用一个Ｐ有一个子局面是Ｎ态,而Ｎ态所有子局面都是Ｐ态的思路进行记忆话搜索,值得注意的是y=x对称的这个操作是没有用的，显然这个操作不会改变和原点的距离,并且如果对手这个操作以后改变了当前局面的Ｎ Ｐ状态的话也可以改回来,由于只能改一次,对于胜负状态没有影响
1 #include<cstdio> 2 #include<iostream> 3 #define maxn 1000 4 using namespace std; 5 int x[maxn],y[maxn],d,n,xx,yy,dp[500][500]; 6 int dfs(int a,int b) 7 { 8 if(a*a+b*b>d*d)return 1; 9 int &u=dp[a+201][b+201]; 10 if(u!=0)return u; 11 for(int i=1;i<=n;i++)if(dfs(a+x[i],b+y[i])==2)return u=1; 12 return u=2; 13 } 14 int main() 15 { 16 scanf("%d%d%d%d",&xx,&yy,&n,&d); 17 for(int i=1;i<=n;i++)scanf("%d%d",&x[i],&y[i]); 18 if(dfs(xx,yy)==1)puts("Anton");else puts("Dasha"); 19 return 0; 20 }
CF 276 D. Little Girl and Maximum XOR
题目大意:在区间[Ｌ，Ｒ]中最大的a^b的值
思路:当时做群赛的时候做的这题,xiaoxin机智的打表得出了答案都是2^n-1的形式,然后只要知道n是多少就行,然后仔细想想就能发现其实就是Ｌ和Ｒ中从高位算起第一位二进制不同的位
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define LLD "%lld" 5 using namespace std; 6 int main() 7 { 8 long long a,b; 9 scanf(LLD LLD,&a,&b); 10 long long cnt=0,n=a^b; 11 while(n>0) 12 { 13 cnt++; 14 n>>=1; 15 } 16 printf(LLD"\n",(1LL<<(cnt))-1); 17 return 0; 18 }
CF 257 B. Playing Cubes
题目大意:有N个蓝木块和M个红木块,两人分别在其中拿出一个放成一排,一人是以最后相邻同色木块数量得分,一人是以相邻不同色木块计分，两人都用最优策略使自己得分最高问最后得分情况
思路:稍微想想就知道最后序列是这样的BRRBBRRBBRRRRRRRRRRR总是以少的那个颜色开头,然后对着这串多看两眼就能想到答案了
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int main() 5 { 6 int a,b; 7 scanf("%d%d",&a,&b); 8 if(a<b)swap(a,b); 9 printf("%d %d\n",a-1,b); 10 return 0; 11 }
CF 343 B. Alternating Current
题目大意:给你两根绳子,弯弯绕,问你最后能不能仅扯着四个线头把两条绳子分开
思路：显然＋＋或者－－这种情况直接可以舍掉的,然后很自然的想到用栈来搞，然后就没有然后了
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<stack> 5 #define maxn 500000 6 using namespace std; 7 stack<int>q; 8 char ch[maxn]; 9 int main() 10 { 11 scanf("%s",ch+1); 12 int len=strlen(ch+1); 13 for(int i=1;i<=len;i++) 14 { 15 char c=ch[i]; 16 if(!q.empty()) 17 { 18 char u=q.top(); 19 if(u==c)q.pop();else q.push(c); 20 } 21 else q.push(c); 22 } 23 if(q.empty())puts("Yes");else puts("No"); 24 return 0; 25 }
