[JZOJ3615]【NOI2014模拟】数列（平面几何+二维线段树）

Description

　　给定一个长度为n的正整数数列a[i]。

　　定义2个位置的f值为两者位置差与数值差的和，即f(x,y)=|x-y|+|a[x]-a[y]|。

　　你需要写一个程序支持2种操作（k都是正整数）：

　　Modify x k：将第x个数的值修改为k。

　　Query x k：询问有几个i满足f(x,i)<=k。询问不仅要考虑当前数列，还要考虑任意历史版本，即统计任意位置上出现过的任意数值与当前的a[x]的f值<=k的对数。（某位置多次修改为同样的数值，按多次统计）

Main

　　令F(x,y)=|x-y|+|a[x]-a[y]|，每次可以将a[x]修改为k，或者查询满足f(x,i)≤k的个数。

Analysis

【二维线段树/树状数组】　　

　　看到题目这样的粗俗，笼统，简洁明了，便知道一定要用一个数据结构维护

　　我们可以将x抽象为x坐标，a[x]抽象为y坐标，那么f(x,y)的意思就显然了：表示x点(x,a[x])和y点(y,a[y])的曼哈顿距离。

　　但是这个曼哈顿距离比较蛋疼，不着急，画（截）个图看看。

　　

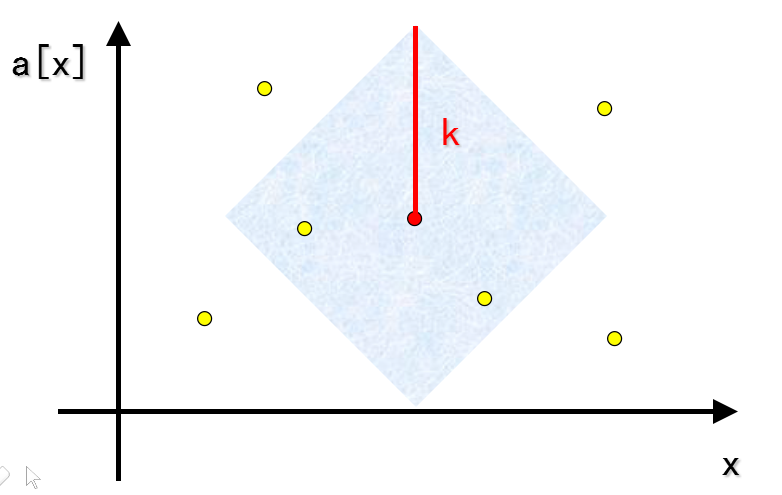
　　我们发现图片大概是这样的，发现这个可以取的范围是个菱形，旋转90°就变成了正方形。旋转就是使坐标(x,y)变成(x+y,x-y)

　　

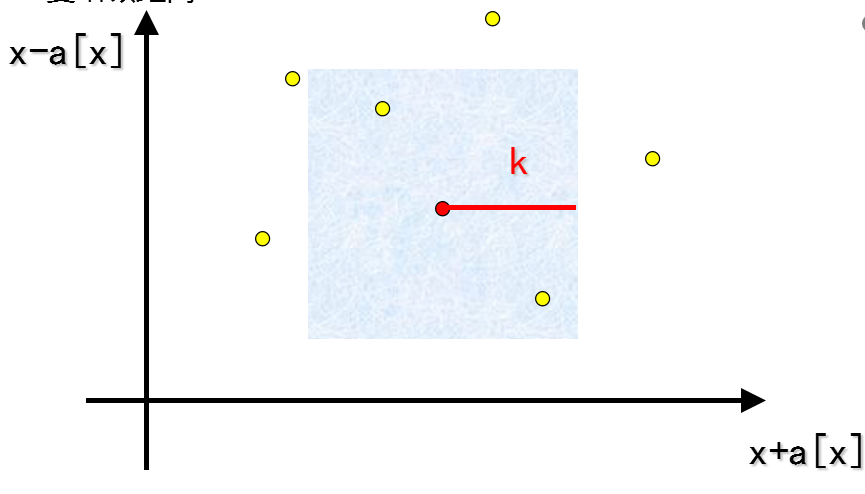
　　那么，问题就转化为每次可以加入一些点，求某个正方形内包含点的个数。

【K-Dtree】

　　。。。

【cbq分治+主席树】

　　...

Solution

　　我们考虑用一个数据结构来维护，如二维线段树/树状数组。

　　每次相当于插入点(x+a[x],x-a[x])到图中，线段树/树状数组维护左下角为(x1,y1)，右上角为(x2,y2)的矩阵信息，查询即可。

　　对于二维线段树，有两种实现方法。一种是划分为4个区域，第二种是划分为2个，根据长宽的大小来切。

　　

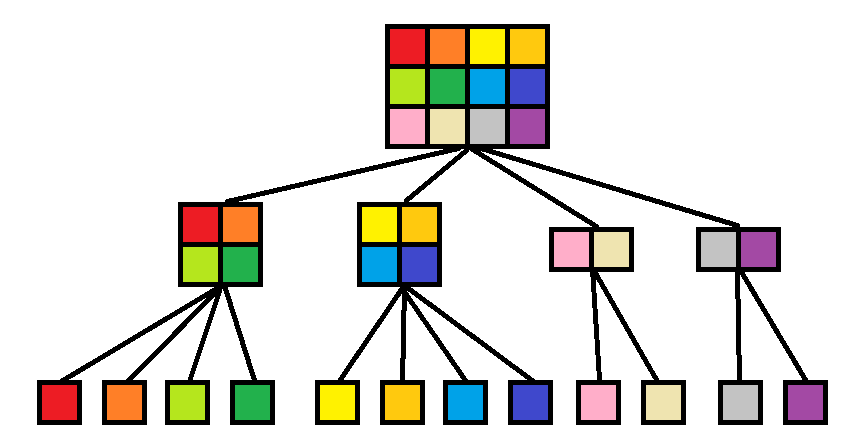
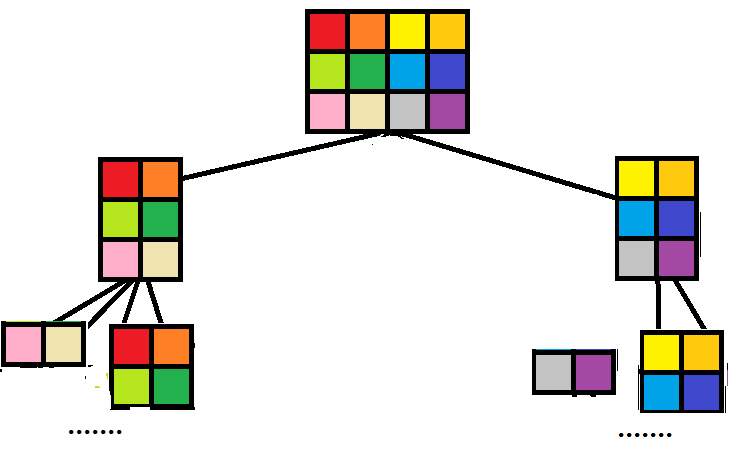
　　要动态开点。直接做会超时，要加优化：当前子树没有贡献，直接退出。

 

【K-Dtree】

 

　　。。。

 

【cbq分治+主席树】

 

　　...

 

Code

{$inline on}
var
        ch,lala:char;
        n,m,i,x,y,tot,ans:longint;
        a:array[0..60000] of longint;
        tree:array[0..2500000] of longint;
        son:array[0..2500000,1..2] of longint;
procedure dispose; inline;
begin
        read(ch);

        lala:='1';
        while lala<>' ' do read(lala);

        readln(x,y);
end;

procedure fyj(x:longint); inline;
begin
        if son[x,1]=0 then
        begin
                inc(tot); son[x,1]:=tot;
                inc(tot); son[x,2]:=tot;
        end;
end;

procedure change(root,x1,y1,x2,y2,fx,fy:longint);  inline;
var
        mid:longint;
begin
        if (x1=x2) and (y1=y2) and (x1=fx) and (y1=fy) then
        begin
                inc(tree[root]);

                exit;
        end;

        fyj(root);

        if x2-x1>=y2-y1 then
        begin
                mid:=(x1+x2) shr 1;

                if fx<=mid then
                        change(son[root,1],x1,y1,mid,y2,fx,fy)
                else
                        change(son[root,2],mid+1,y1,x2,y2,fx,fy);
        end
        else
        begin
                mid:=(y1+y2) shr 1;

                if fy<=mid then
                        change(son[root,1],x1,y1,x2,mid,fx,fy)
                else
                        change(son[root,2],x1,mid+1,x2,y2,fx,fy);
        end;

        tree[root]:=tree[son[root,1]]+tree[son[root,2]];
end;

procedure find(root,x1,y1,x2,y2,fx1,fy1,fx2,fy2:longint);  inline;
var
        mid:longint;
begin
        if (x1=fx1) and (x2=fx2) and (y1=fy1) and (y2=fy2) then
        begin
                ans:=ans+tree[root];

                exit;
        end;

        if son[root,1]=0 then
                exit;

        if x2-x1>=y2-y1 then
        begin
                mid:=(x1+x2) shr 1;

                if fx2<=mid then
                        find(son[root,1],x1,y1,mid,y2,fx1,fy1,fx2,fy2)
                else
                if fx1>mid then
                        find(son[root,2],mid+1,y1,x2,y2,fx1,fy1,fx2,fy2)
                else
                begin
                        find(son[root,1],x1,y1,mid,y2,fx1,fy1,mid,fy2);
                        find(son[root,2],mid+1,y1,x2,y2,mid+1,fy1,fx2,fy2);
                end;
        end
        else
        begin
                mid:=(y1+y2) shr 1;

                if fy2<=mid then
                        find(son[root,1],x1,y1,x2,mid,fx1,fy1,fx2,fy2)
                else
                if fy1>mid then
                        find(son[root,2],x1,mid+1,x2,y2,fx1,fy1,fx2,fy2)
                else
                begin
                        find(son[root,1],x1,y1,x2,mid,fx1,fy1,fx2,mid);
                        find(son[root,2],x1,mid+1,x2,y2,fx1,mid+1,fx2,fy2);
                end;
        end;
end;
begin                   
        readln(n,m);

        tot:=1;

        for i:=1 to n do
        begin
                read(a[i]);

                change(1,0,0,320000,280000,i+a[i]+100000,i-a[i]+100000);
        end;

        readln;

        for i:=1 to m do
        begin
                dispose;

                if ch='M' then
                begin
                        change(1,0,0,320000,280000,x+y+100000,x-y+100000);

                        a[x]:=y;
                end
                else
                begin
                        ans:=0;
                        find(1,0,0,320000,280000,x+a[x]-y+100000,x-a[x]-y+100000,x+a[x]+y+100000,x-a[x]+y+100000);

                        writeln(ans);
                end;
        end;
end.