QUEKI的晨读小本本

【搜索、模拟、枚举暴力、贪心、最短路spfa、dijkstra、动态规划、最近公共祖先、最小生成树\】

一。咕咕咕···n个点n-1条边的无向连通图一定是一棵树

二。判断有没有负环——两种判法：

1.记录此点被更新了多少次，更新次数大于N就有负环.这意味着一个点被重复迭代超过N次，显然有负环.

2.记录从S到当前点路径上经过了多少个点，超过N则有负环.这张图才有N个点，一条路径上没有重复点经过点数是<= N的，所以有负环.

三。#### 欧拉函数是从1开始算的，1和1互质（\(φ(1)=1\)）

四。#### 字符串比较（compare(st,end,string2)）和替换replace

#include<cstdio>
#include<iostream>
#include<string>
using namespace std;
const int N=2e6+10, M=11;
int step[N];
string a,b,s1[M],s2[M],q[N]; 
int main(){
	ios::sync_with_stdio(false);
    int n=1;
    cin >> a >> b;
    while(cin >> s1[n] >> s2[n]) n++;
    n--;//处理变换规则 
    int h = 0, t = 1;
    q[1] = a;
    while(h < t){
        if(step[++h] > 10) break;
        
        for(register int i = 1; i <= n;++i){   
            for(int j = 0; j < q[h].length(); ++j){
                if(!q[h].compare(j,s1[i].length(),s1[i])){//如果包含给出的串
                    q[++t] = q[h];
                    step[t] = step[h] + 1;
                    q[t].replace(j,s1[i].length(),s2[i]);
                    if(q[t] == b){
                        cout << step[t];
                        return 0;
                    }
                }
            }
        }
    }
    cout<<"NO ANSWER!";
    return 0;
}

uva156反片语

主要内容（reciting content）：map，字符串

#include <cstdio>
#include <map>
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int len;
map<string,int> mp;
char s[25];
string word[1005],now;
int main()
{
    cin >> now;
    while(now!="#"){ //输入 
        for(int i=0;i<now.size();i++){
            s[i]=now[i];
            if(s[i]>='a'&&s[i]<='z'){
                s[i]=s[i]-'a'+'A';
            }
        }//s存了now的全大写形式 
        word[++len]=now;  //
        sort(s,s+now.size());  //将该单词按字典序排序 
        now="";  //字符串清空 
        for(int i=0;i<word[len].size();i++)  now+=s[i];  
        if(mp.count(now)==0)  //单词字典序排序  （0表示不存在，1表示存在 
            mp.insert(pair<string,int>(now,0));
        mp[now]++;
        cin>>now;
    }
    
    sort(word+1,word+1+len);  //将所有单词按字典序排序
	 
    for(int i=1;i<=len;i++){
        now = word[i];
        for(int j = 0; j < now.size(); j++){
            s[j] = now[j];
            if(s[j] >= 'a' && s[j] <= 'z'){
                s[j]=s[j]-'a'+'A';
            }
        }
        sort(s,s+now.size());
        now="";
        for(int j=0;j<word[i].size();j++){
            now+=s[j];
        }
        if(mp[now]==1){//如果只有它一个，那么就输出
            cout<<word[i]<<endl;
        }
    }
    return 0;
} 

五。#### gcd相关

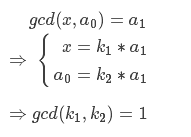
k1,k2互质

六。#### 时间相关
printf("Time used = %.2f\n", (double)clock() / CLOCKS_PER_SEC);

七。#### 各种优化写法
①模运算

inline void Add(int &x,int y) { (x+=y)>=p&&(x-=p); }

这事实上等价于 x=(x+y)%p 

五。三元环、四元环

三元环计数

给定一个\(n\)个点\(m\)条边的无向图，问有多少个三元组\((u,v,w)\)满足两两之间有边相连。
我们先把无向图转成有向图，并给每个点定义一个双关键字\((deg_i,id_i)\)，其中\(deg\)表示度数，\(id\)表示标号，这样对于每一对点都能严格比较出大小。

我们把每一条边重定向成从度数大的点连向度数小的点，我们就可以得到一张有向无环图。

枚举一个点\(i\)，将所有\(i\)点连出的点标记为\(i\)。
枚举一个\(i\)连出的点\(j\)。
枚举一个\(j\)连出的点\(k\)，如果\(k\)的标记是\(i\)，那么就找到了一组三元环\((i,j,k)\)。
分析每一个三元环只会在ii这个点被算到一次答案。

四元环计数

先和三元环一样，把每个点排出来rank。

然后枚举两条边，找每个点距离2的点x，将x的标记加入答案，然后往上面标记+1