PA2014-Final Zarowki（堆）

题目大意 

 

解题报告

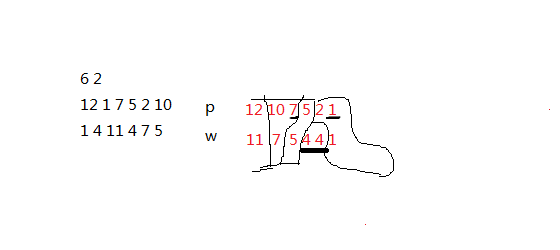
• （题意）拥有的灯泡功率必须大于等于需要的，有k次机会换拥有的功率
• 换的次数少于 需要换的灯泡数 时，输出NIE无解
• 并不是一一对应的关系，因为这个灯泡 可能其他拥有的灯泡可以 满足，而功率数可能更小； 也有可能没有灯泡可以给他用；
• 所以我们应当把 能满足大功率灯泡中 较小功率的灯泡 给大需求用户，而不是给一个需求量更小的灯泡（如样例中（拥有）7应该给（需求）7而不应该给（需求）5）
• “小的灯泡能用则用，不能用的保留”

#include<bits/stdc++.h>
using namespace std;

#define fr(i,z) for(int i = 1; i <= z; i++)

const int N = 500500;
int n,k,j = 1;
int p[N],w[N];
long long ans;

priority_queue<int > t;
priority_queue<int,vector<int>,greater<int> > q;

bool cmp(int a,int b){return a>b;}  

int main()
{
    scanf("%d%d",&n,&k);
    fr(i,n)   scanf("%d",p + i);    
    fr(i,n)   scanf("%d",w + i);  
    sort(p + 1, p + n + 1, cmp);
    sort(w + 1, w + n + 1, cmp); //要从大到小比较，为了获得能满足要求的最小功率的灯泡
    
    fr(i,n){
        while(p[j] >= w[i])   q.push(p[j++]);  //把可以满足的都扔进堆里
        
        if(!q.empty()){  
            ans += q.top();  
            t.push(q.top() - w[i]);  //要记下差值，以便后面换灯泡
            q.pop();
            continue;
        }
         
        k--;  //计数，判断是否无解 以及 最后剩余的可更换数
        ans += w[i];  //如果确定要换，那肯定是换等于需求功率的
        if(k < 0) {   //判断无解
        cout << "NIE";
        return 0;
        }
    }
    while(k--){  
        ans -= t.top();  //换的思路都是相同的
        t.pop();
    }
    cout << ans;
}

 

看官老爷们可以散了下面是蒟蒻的错题记录了_(:3_|/_)__

---

 

 错解

为了长个记性贴一下自己一开始写的错解

/*6 2
12 1 7 5 2 10
1 4 11 4 7 5 */
//没改完的灯泡
#include<bits/stdc++.h>
using namespace std;
#define fr(i,n)  for(int i = 1; i <= n; i++)
const int N = 500050;
int n,k,ans,sum,len;
int p[N],w[N];
struct node{
    int nd, as, yy;   //as绝对值，nd需要的功率，yy拥有的 
    bool operator <(const node &b)const{
      return as > b.as;
    }
}t;
priority_queue<node>q; //大根堆 

int main()
{
  scanf("%d%d",&n,&k);
  fr(i,n) {
  scanf("%d",p + i);
  ans += p[i];
  } 
  fr(i,n) scanf("%d",w + i);
  
  sort(p, p + n + 1);
  sort(w, w + n + 1);
  
  fr(i,n){
      if(p[i] < w[i]){
       ans = ans - p[i] + w[i];
       p[i] = w[i];
       sum++;
       continue;
        } 
    t.nd = w[i], t.as = abs(p[i] - w[i]), t.yy = p[i]; 
    q.push(t);
    }    
    
  if(sum > k){
      cout << "NIE";
      return 0;
  }
  
   int sy = k - sum;  //还剩下的修改次数 
   for(int i = 1; i <= sy; i++){
       ans -= q.top().yy + q.top().nd;
   }

  cout << ans;
  return 0; 
}

这份代码错的原因是 没有考虑使用拥有的其他灯泡（不是一一对应）可能会更优， 其他部分的代码还是有可以的地方的； 

上面（正解）容易错（或者想不通）的地方在于：有些情况下 去商店换灯泡可能是比使用其他灯泡更优的。