试题一
输入包含多组测试数据,第一行输入测试数组的数量n,其中n小于等于10^5。接下来的再输入2*n个数,每个数为小于等于10^9的非0正数。组成一个长度为2n的数组。接下来每次在数组中取两个数,组成一个坐标并且将其绘制在平面坐标系上面(一共可以取n次)。再用一个矩形去围住这些点,选择一种取数方式,要求最后得到的矩形的面积最小。输出最小的面积即可。
输入样式:
2
1 2 3 5
输出样式:
2
算法思路
每一次测试的数据量最多为10^5,因此不适合用蛮力法(蛮力法通常至少包含两个循环)。进一步分析,题目只要求输出最小矩形的面积,由此想到对问题转化。要使面积最小,实际上就是矩形长乘以宽要最小。因此可以考虑贪心策略。使长和宽尽量都小。而矩形的长(宽)是由所有的坐标中横(纵)坐标最大值减去最小值的查决定的,为了使这个值最小,可以先对数组从小到大排序,排完序之后的数组a的长度为2n。则此时最小的面积应当为:(a[2n-1]-a[n])*(a[n-1]-a[0])。值得注意的是a[2n-1]-a[n]或者a[n-1]-a[0]的值可能为0,此时应当进行特殊处理,将为0的值替换为1(因为矩形长和宽最短的情况下应该为1)【当时上级的时候没想到这种情况,导致后面提交通过率一直是87%左右😅😅】
算法代码
package basic_language.byte_dance;
import java.util.Arrays;
import java.util.Scanner;
/**
* 第一行输入n
* 第二行输入2n个数据
* 对这2n个数据进行划分,分成n个坐标对,用一个矩形在xy坐标系下围住这些点,求矩形最小的面积
*/
public class Test1 {
public static void main(String[] args) {
int n;
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextLine()) {
// 接收用户的输入
n = scanner.nextInt();
int[] array = new int[2 * n];
for (int i = 0; i < 2 * n; i++) {
array[i] = scanner.nextInt();
}
// 只有一个点直接返回1
if(n==1) {System.out.println(1);continue;}
Arrays.sort(array);
if(array[2*n-1]-array[n]==0){
if(array[n-1]-array[0] ==0){
System.out.println(1);
}else{
System.out.println(array[n-1]-array[0]);
}
}else{
long result= (array[2*n-1]-array[n])*(array[n-1]-array[0]);
System.out.println(result==0L? array[2*n-1]-array[n] : result);
}
}
}
}
点评
第一题实际上玩了一个智力游戏,脑子灵活一点很容易想到思路。注意对应的细节即可
试题二
接收如下的输入,第一行输入n,n<=10^5。第二行输入n个数,每一个数的范围0<=n<=10^9。在里面找到连续的子数组,使其成为3和5的倍数但不是4的倍数,输出满足该条件的所有子数组的数量。
输入样例:
3
1 14 15
输出样例:
3
说明:三个子数组分别是[1,14],[15],[1,14,15]
算法思路
首先排除蛮力法,对于较小的n值(小于等于1000),用蛮力法还是可以应对的。但是当n的值比较大的时候,使用蛮力法将浪费大量的时间(后面会有对比)。因此我们需要转变思路,从蛮力法开始思考。蛮力法之所以比较浪费时间,是因为需要反复计算某个区间的元素之和。例如计算a[1]+a[2]+a[3]+a[4]同时也包含子数组a[2]+a[3]+a[4]的计算,因此重复的计算太多了。这是算法大忌。因此我们需要减少重复计算的次数,减少代码执行时间。一种典型的思路就是以空间换时间。
- 申请长度为n的数组sums,其中sums[i]=a[0]+a[1]+...+a[i]。之所以这样设计,是因为假设后面需要求解区间[i+1,j]的元素之和,只需要使用sums[j]-sums[i]即可(如果不好理解随便举个例子即可)
- 但是1中的方式还是避免不了要重复遍历sums数组,因为为了判断从下标0开始的子数组中元素之和满足输出要求的需要一直遍历到sums数组末尾。同理为了判断从下标1开始的子数组中元素之和满足输出要求的也需要一直遍历到sums数组末尾,实际上代码的复杂度还是O(N^2),还是不可以接受。
- 正当我苦思冥想的时候,突然想到模运算的相关运算规则,如下:
a%x - b%x ==0 <=> (a-b)%x==0
上面的式子证明比较简单,这里就不证明了。【当时在考试的时候,我还在为我的急中生智而窃喜,脑子怎么这么灵活,是吧。后来考试结束,我在网上一搜,原来这是一种常用的技巧,只不过是我之前不知道罢了。我真的裂开!😋😋】
现在就是神来之笔了,既然有上面的等式。那我们可以按照如下的方式充分运用上面的等式:
- 申请长度为15的数组temp,其中temp[i]表示值为i的元素的个数。初始化temp数组的时候,temp[sums[i] % 15]++。即遍历sums数组,将数组中的每一个元素模15之后作为下标更新temp数组,这样temp[i]中记录的都是sums数组中模15的值都是i的元素的个数。再回到那个等式:
a%x - b%x ==0 <=> (a-b)%x==0
猜猜我想到了什么,假设b,c,d是整个sums数组中模15等于i的数,那么此时temp[i]应该等于3。而此时满足题目输出要求的子数组的和应当为:
c-b, d-b, d-c, 相应在这一步应当更新最终返回结果加三。这不就是在a,b,c三个数之中任取两个数相减,并且保证相减的时候是大减小。这不就是排列组合吗?老天爷!因此实际上我们根本不用关系子数组的和是多少。
- 只需要知道temp[i]的值,从而更新最后结果加上
上面用到了高中排列组合知识,也就是大学概率论里面的古典概型
接下来需要解决的问题就是处理不能被4整除,此时肯定不能用上面的那个等式。此时需要脑子灵活一点,逆向思维
通过temp求得满足题目输出条件的result之后,接下来肯定需要减去某个数以排除能整除4的数,但是应该怎么排除呢。实际上很简单,即在能整除15的字数组中排除那些能够被4整除的子数组。
- 按照4和5中的思路,再申请一个长度为60的数组temp2,temp2[i]中记录的都是sums数组中模60的值都是i的元素的个数,这样我们就找到能够整除60的子数组的数量,记为result1。【为什么是60呢?为什么不是4呢。如果是4,此时temp2[i]中记录的都是sums数组中模4的值都是i的元素的个数,而在这些数中有一些是不能被15整除的,因此我们需要满足基本条件被15整除,通过下面的韦恩图可以更好的理解】

- 最终返回的结果是result-result1。即在能整除15的字数组中排除那些能够被4整除的子数组
算法代码
package basic_language.byte_dance;
import java.util.Random;
import java.util.Scanner;
/**
* 第一行输入n,n<=10^5
* 第二行输入n个数,每一个数的范围0<=n<=10^9
* 在里面找到连续的子数组,使其成为3和5的倍数但不是4的倍数,输出满足该条件的所有子数组的数量
*/
public class Test2 {
public static void main(String[] args) {
int n;
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
n = scanner.nextInt();
// 接收输入
int[] array = new int[n];
for (int i = 0; i < n; i++) {
array[i] = scanner.nextInt();
}
// 使用额外一个数组记录元素之和,数组名称为sums,其中sums[i]的含义为:a[0]+a[1]+...+a[i]
long[] sums = new long[n];
sums[0] = array[0];
for (int i = 1; i < n; i++) {
sums[i] = sums[i - 1] + array[i];
}
// 处理子数字长度为1的情况,正如步骤1中提到的那样:
// 求解区间[i+1,j]的元素之和,只需要使用sums[j]-sums[i]即可
// 求解以0为开头的区间需要单独考虑
long result = 0;
for (int i = 0; i < n; i++) {
if (sums[i] % 15 == 0 && sums[i] % 4 != 0) {
result++;
}
}
// 申请长度为15的数组temp,temp[i]的含义是值为i的元素的个数
// 将sums数组中的元素模15后加入temp当中
int[] temp = new int[15];
for (int i = 0; i < n; i++) {
temp[(int) (sums[i] % 15)]++;
}
// 遍历temp,如果temp[i] !=0 则临时结果result加上(temp[i]-1)*temp[i]/2
for (int i = 0; i < 15; i++) {
result += temp[i] * (temp[i] - 1) / 2;// 这里需要注意细节,很重要,先算乘法再算处罚。否则按照Java语言规则,如果a不能整除b有余数的话,Java会自动向下取整。造成数据丢失。实际上就是一个小细节需要注意
}
// 再申请长度为60的数组temp2,temp2[i]的含义是值为i的元素的个数
int[] temp2 = new int[60];
for (int i = 0; i < n; i++) {
temp2[(int) (sums[i] % 60)]++;
}
// 将sums数组中的元素取模60加入到temp2中
// 遍历temp2,如果temp2[i] !=0 则临时结果result减去(temp2[i]-1)*temp[i]/2
for (int i = 0; i < 60; i++) {
result -= temp2[i] * (temp2[i] - 1) / 2;
}
System.out.println(result);
}
}
}
进一步思考:和蛮力法比较
在上面代码的基础上,新增如下两个方法:
/**
* 随机生成长度为length的数组
*
* @param length
* @return
*/
private static int[] generate(int length) {
int[] array = new int[length];
Random random = new Random();
for (int i = 0; i < length; i++) {
array[i] = random.nextInt(length);
}
return array;
}
/**
* 暴力求解该问题,适用于array长度较小的情况
* 每隔5秒打印依次程序运行情况
*
* @param array
*/
private static void violentSolve(int[] array) {
long currentTime = System.currentTimeMillis();
int times = 1;
long result = 0;
for (int i = 0; i < array.length; i++) {
for (int j = i; j < array.length; j++) {
// 计算从[i,j]之和
long sum = 0;
for (int k = i; k <= j; k++) {
sum += array[k];
}
if (sum % 15 == 0 && sum % 4 != 0) {
result++;
}
long millis = System.currentTimeMillis();
while (millis - currentTime > 5 * 1000 * times) {
System.out.print("蛮力法程序已经运行的时间,单位为秒:" + (millis - currentTime) / 1000.0);
System.out.println(";处理的区间为[ " + i + "," + j + " ]");
times++;
}
// 超过5分钟程序还没执行完,终止循环
if (millis - currentTime >= 5 * 60 * 1000) {
System.out.print("使用蛮力法求解出来的值:" + result);
return;
}
}
}
System.out.print("使用蛮力法求解出来的值:" + result);
System.out.println("。所用的时间为:" +(System.currentTimeMillis()-currentTime)/1000.0);
}
上面的暴力求解方法将在程序执行过程中每隔5秒打印一次程序运行状态,和按照以空间换取时间算法相比,执行结果如下:
比较结果
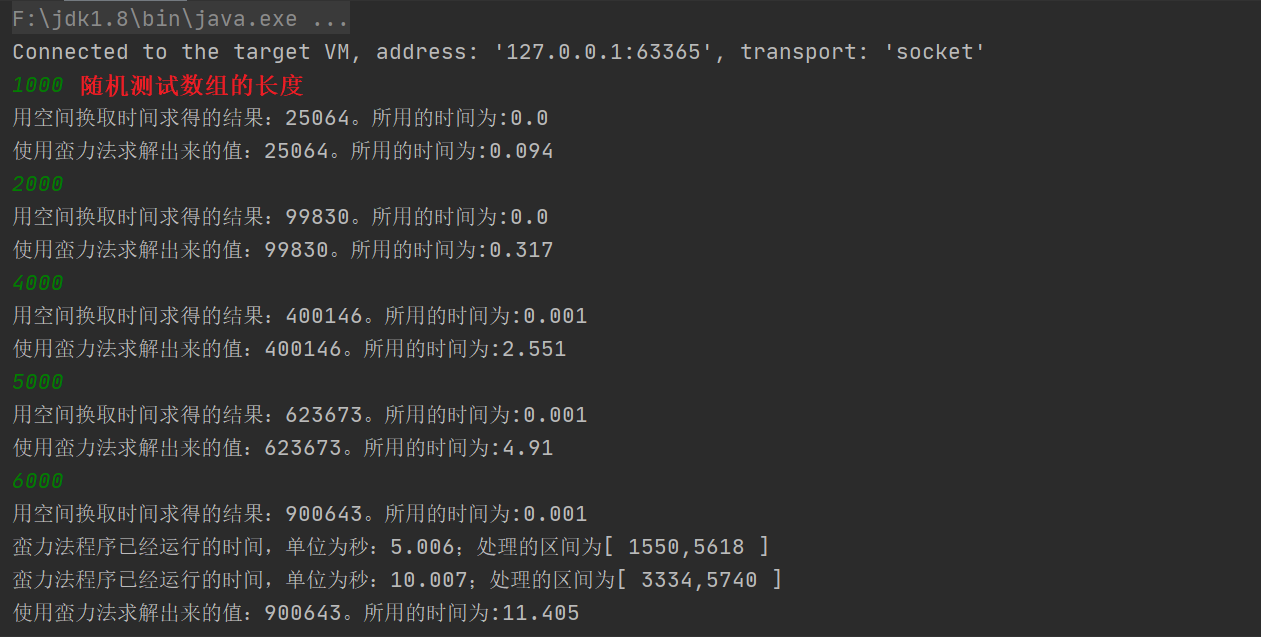
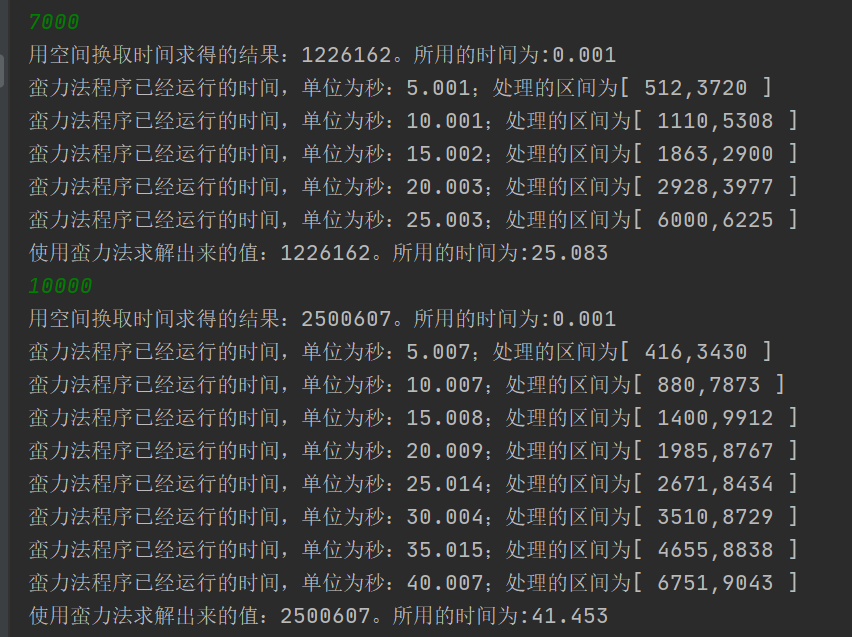





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通