【PAT】1053 Path of Equal Weight（30 分）

1053 Path of Equal Weight（30 分）

Given a non-empty tree with root R, and with weight W​i​​ assigned to each tree node T​i​​. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.

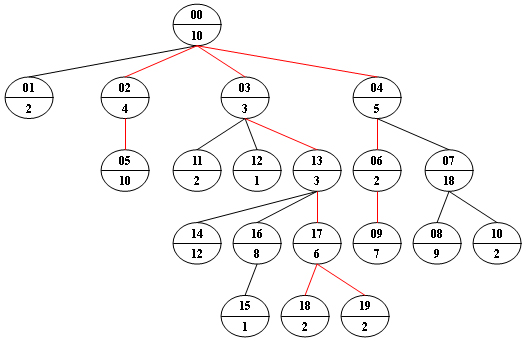
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let's consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0<N≤100, the number of nodes in a tree, M (<N), the number of non-leaf nodes, and 0<S<2​30​​, the given weight number. The next line contains N positive numbers where W​i​​ (<1000) corresponds to the tree node T​i​​. Then M lines follow, each in the format:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 00.

Output Specification:

For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.

Note: sequence {A​1​​,A​2​​,⋯,A​n​​} is said to be greater than sequence {B​1​​,B​2​​,⋯,B​m​​} if there exists 1≤k<min{n,m} such that A​i​​=B​i​​ for i=1,⋯,k, and A​k+1​​>B​k+1​​.

Sample Input:

20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19

Sample Output:

10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2

C++代码如下：

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
#define maxn 105

struct Node {
    int weight;
    vector<int>child;
};

int n, m, s;
Node num[maxn];

bool cmp(int a, int b) {
    return num[a].weight > num[b].weight;
}

vector<int>v;   //存放路径对应的权值
void path(int r,int sum) {
    if (sum > s) {
        v.pop_back(); return;
    }
    if (sum == s) {
        if ( num[r].child.size() == 0) {
            cout << v[0];
            for (vector<int>::iterator it = v.begin() + 1; it != v.end(); it++)
                cout << ' ' << *it;
            cout << endl;
            v.pop_back();
            return;
        }
        else {
            v.pop_back(); return;
        }
    }
    for (int i = 0; i < num[r].child.size(); i++) {
        int t = num[r].child[i];
        v.push_back(num[t].weight);
        path(t, sum + num[t].weight);        
    }
    if (!v.empty()) v.pop_back();
}
int main() {
    cin >> n >> m >> s;
    int w;

    for (int i = 0; i < n; i++) {
        cin >> w;
        num[i].weight = w;
    }
    int id,k,t;
    for (int i = 0; i < m; i++) {
        cin >> id>>k;
        for (int j = 0; j < k; j++) {
            cin >> t;
            num[id].child.push_back(t);
        }
        sort(num[id].child.begin(), num[id].child.end(), cmp);
    }
    v.push_back(num[0].weight);
    path(0,num[0].weight);
    return 0;
}