五、优化模型
5.1 使用测试集评估模型性能
- 划分训练集和测试集,比例:8/2, 7/3
![]()
- 计算Jtest 、Jtrain 衡量模型在测试集合训练集上的、不包括正则化项
- 对于线性回归问题:
- 对于分类问题
Jtest(W,b)是测试集中被错误分类的部分。
Jtrain(W,b)是训练集中被错误分类的部分。
5.2 模型选择 \ 交叉验证集
一旦参数w,b被拟合到训练集,训练误差Jtrain(W,b)就可能低于实际的泛化误差(虽然通过训练模型的参数可以使训练误差很低,但这并不意味着模型对新数据的预测同样准确。)。Jtest(W,b)比Jtrain(W,b)能更好地估计模型对新数据的概括程度。

1 训练集train用来训练参数w和b,而测试集test用来选择多项式模型(即参数d),训练集不能评估w和b的好坏,类似的测试集也不能用来评估参数d的好坏。w,b与d一样都是经过学习得到的,那么当然都会存在一些问题。
2 根据测试集误差选择的参数d,所以可能是乐观估计。一个只考虑到训练集误差Jtrain,一个只考虑到测试集误差Jtest,都不全面,所以是乐观预测
- 交叉验证集、开发集、验证集 dev set
![]()
![]()
![]()
![]()
理解:先通过训练集拟合w,b. 然后通过交叉集选择出最优的模型也即参数d,最后用选择出来的模型在测试集中估计泛化能力
就是一个训练参数wb,一个挑选最合适的一个模型,test用来算误差(敲定最终模型,才能在test集中评估)
5.3 偏差 方差 bias variance
计算Jtrain Jcv 比较大小,来判断算法是否高偏差、高方差
在统计学和机器学习中,偏差指的是模型预测值与真实值之间的差距,方差指的是模型对不同训练数据集的敏感度,即模型预测的波动程度。
在机器学习中,一个常见的目标是在高偏差和高方差之间取得平衡,以达到最佳的泛化性能。
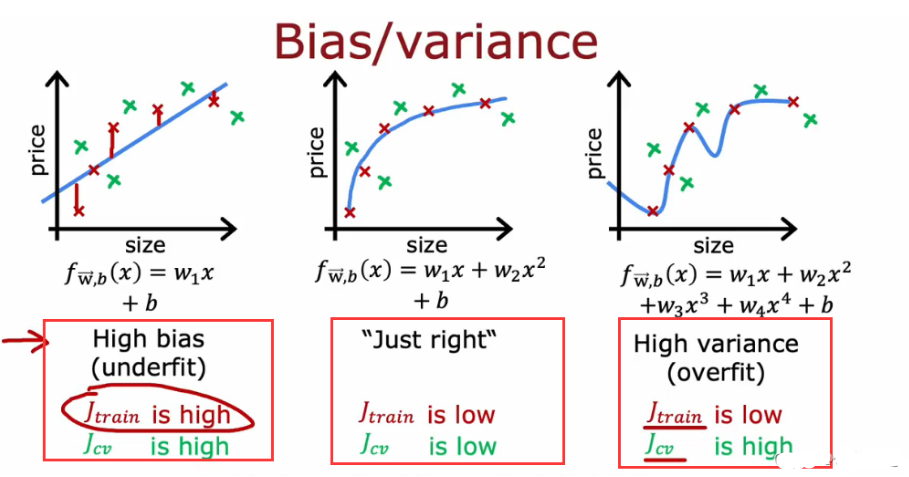
- 从Jtrain 和Jcv 大小来理解 偏差和方差
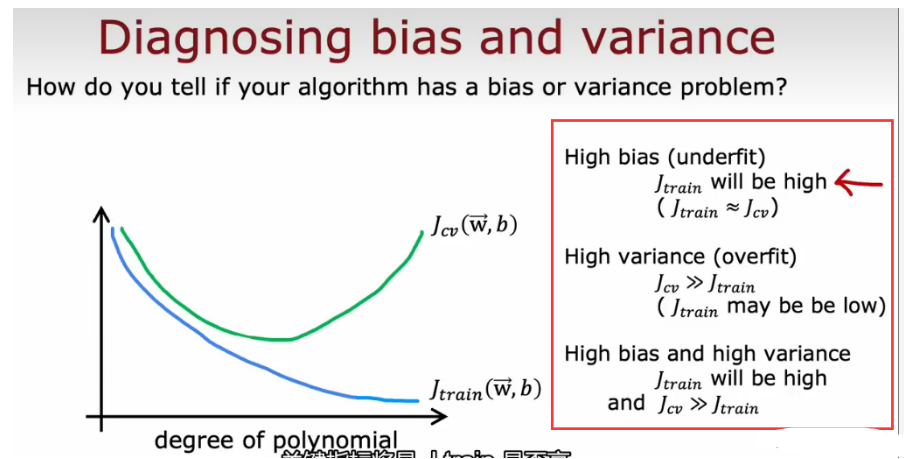
- 另一个角度 高次项大小
当高次项越来越大时候,Jtrain会下降;次项太小,欠拟合,jcv很大在交叉验证集上效果不好,当次项太大,过拟合,jcv也很大,在中间
高偏差的学习曲线特征
- 训练误差和验证误差都高,并且两个曲线之间的间隙较小。
- 训练误差和验证误差趋于平稳,且保持在较高的水平。
![]()
![]()
5.4 正则化参数lamda对 偏差、方差影响以及如何利用 交叉验证 选正则化参数lamda
正则化如何影响算法的偏差和方差,什么时候应该使用正则化?
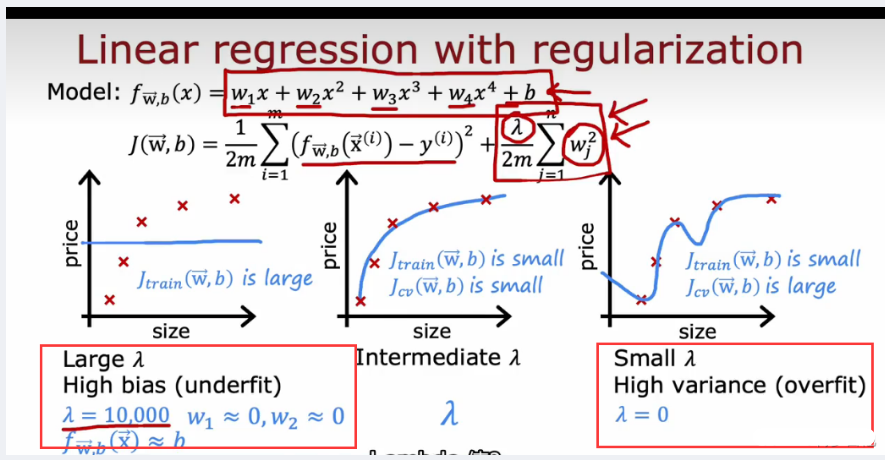
- 当lamda 很大,算法视图保持w2越小,导致参数很接近0,最后模型就会接近fx = b ,欠拟合
- 当lamda很小,极端点为0,就变成了没有正则化化的损失函数J,会过拟合如何选择lamda ?,利用交叉验证
- 利用交叉验证集Jcv来选择lamda
![]()
类似模型选择,从lamda=0开始计算Jtrain拟合出wb参数,然后在交叉验证集cv上计算Jcv误差,每次把lamda变大2倍, 选择最小的,最后在test测试集评估Jtest,达到泛化
- 从Jcv -Jtrain —— lamda 图像理解
![]()
- 过小的 λ会导致模型过拟合,方差高,训练误差低,但验证误差高。
- 过大的 λ会导致模型欠拟合,偏差高,训练误差和验证误差都高。
- 在适中的 λ值(图中标记的最佳 λ点),模型的训练误差和验证误差之间的差距最小,模型的泛化能力最佳。这就是偏差-方差权衡的最佳点。
5.5 指定一个用于性能评估的基准 baseline 来判断是否有高偏差、方差的情况

5.6 添加更多数据的技巧
数据增强
- 对于图像数据:扭曲
- 对于音频数据:添加噪声
数据合成
一般用于计算机视觉干扰

5.7 迁移学习 transfer learning(监督预训练)
作用:让你用来自不同任务的数据来解决当前的任务
- eg:把动物识别模型迁移到0-9数字识别
![]()
- 微调方法一(训练集很小)
前4个参数仍然保留,只需要更新输出层的参数,利用gd 或者adam优化算法来最小化代价函数 - 微调方法二(训练集很大)
重新训练所有参数,但前四层的参数还是用上面的值作为初始值!
1.因为两个模型的本质都是图像分类,所以在隐藏层的大部分工作都是相似甚至一样的
2.所以直接把第一个网络的隐藏层拿过来用,对输出层重新训练就能实现新的功能
3.相当于螺丝刀的刀柄都是一样的,但把十字刀刀头换成一字刀作用就不一样了
下面的图可以帮你理解迁移学习的原理:

神经网络每一层训练它学会检测边缘、拐角、曲线和基本形状
- 预训练
监督预训练supervised pretraining:首先在大型数据集上进行训练,然后在较小的数据集上进行进行参数微调(fine tuning)利用已经初始化的或者从预训练模型获取的参数,运行gd,进一步进行微调权重,以适应手写数字识别任务
什么是微调?可以这样理解,你下载了别训练好的神经网络,自己使用更小的数据集50-100张等,来训练这个网络
5.8 倾斜数据集的误差指标 Error metrics for skewed datasets
-
数据倾斜
某个类别的样本数只有另一个类别的1/10,这个数据集就是倾斜的。这种情况也常常出现在诸如诈骗检测、医学诊断、罕见事件预测等领域中,因为这些问题中正例(positive)的数量通常比负例(negative)少得多。 -
例子: 罕见症预测

5.8.1 精确率和召回率 Precision/ recall 、混淆矩阵
对于这个罕见病识别的例子:
精确率:就是预测为阳性的病人中 真正为阳性的人的比例(找的对 )
召回率:在所有患有罕见病的人中,我们真正正确检测的比例(阳了的人,有多少被正确的检测出来了,找的全)

在医学诊断领域中,通常更关注召回率,因为漏诊罕见病患者可能会导致严重后果
- 混淆矩阵

5.8.2 精确率(找的对)和召回率(找的全)的权衡、F1score
我们将患病的样本标记为正类,未患病的样本标记为负类。在这种情况下
- 1. 手动选择一个阈值来权衡精度和召回率
-
- 如果治病的代价很大,患病后果不难么严重,只在我们十分有把握的情况下去预测y=1,设置更高的阈值(如0.7),这样precision会增加(因为是十分有把握,找的对的概率大了);recall会减少(假阴性FN的结果增多,即实际患病的样本被错误地判断为未患病),
- 另一方面,如果我们不想漏掉罕见病病例,治疗风险不大,但不治疗的结果很坏,可以减低阈值,结果跟上面相反

- 2. F1 score 自动权衡精度和召回率,
F1 score(F1值)是一种综合评价分类器性能的指标,结合了分类器的准确率和召回率。它是准确率和召回率的调和平均数(取平均值的方法,更强调较小的值),通常用于评估二元分类器的性能。

在计算 F1 score 时,精确率和召回率对结果的贡献是一样的。因此,F1 score 强调了精确率和召回率同等重要。当精确率和召回率差异较大时,F1 score 的值会受到最小值的影响。例如,当精确率很低但召回率很高时,F1 score 的值会受到精确率的影响而降低,因为 F1 score 考虑了两者的平均值。
5.9 课后作业
# 1 Regularized Linear Regression 正则线性回归
# 在前半部分的练习中,你将实现正则化线性回归,以预测水库中的水位变化,从而预测大坝流出的水量。
# 在下半部分中,您将通过一些调试学习算法的诊断,并检查偏差 v.s. 方差的影响。
# 1.1 Visualizing the dataset
# 我们将从可视化数据集开始,其中包含水位变化的历史记录,x,以及从大坝流出的水量,y。
# 这个数据集分为了三个部分:
# training set 训练集:训练模型
# cross validation set 交叉验证集:选择正则化参数
# test set 测试集:评估性能,模型训练中不曾用过的样本
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
import scipy.optimize as opt
data = loadmat('ex5data1.mat')
# Training set
X, y = data['X'], data['y']
# Cross validation set
Xval, yval = data['Xval'], data['yval']
# Test set
Xtest, ytest = data['Xtest'], data['ytest']
X = np.insert(X, 0, 1, axis=1)
Xval = np.insert(Xval, 0, 1, axis=1)
Xtest = np.insert(Xtest, 0, 1, axis=1)
print('X={},y={}'.format(X.shape, y.shape))
print('Xval={},yval={}'.format(Xval.shape, yval.shape))
print('Xtest={},ytest={}'.format(Xtest.shape, ytest.shape))
# X=(12, 2),y=(12, 1)
# Xval=(21, 2),yval=(21, 1)
# Xtest=(21, 2),ytest=(21, 1)
def plotData():
plt.figure(figsize=(8, 5))
plt.scatter(X[:, 1:], y, c='r', marker='x')
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam(y)')
plt.grid(True) # 开启网格线
# plt.show()
# plotData()
# Regularized linear regression cost function
def costReg(theta, X, y, l):
'''do not regularizethe theta0
theta is a 1-d array with shape (n+1,)
X is a matrix with shape (m, n+1)
y is a matrix with shape (m, 1)
'''
cost = ((X @ theta - y.flatten()) ** 2).sum()
regterm = l * (theta[1:] @ theta[1:])
return (cost + regterm) / (2 * len(X))
theta = np.ones(X.shape[1])
print(costReg(theta, X, y, 1)) # 303.9931922202643
# 1.3 Regularized linear regression gradient
def gradientReg(theta, X, y, l):
"""
theta: 一维数组,形状为 (2,)
X: 二维数组,形状为 (12, 2)
y: 二维数组,形状为 (12, 1)
l: 正则化参数 lambda
grad 的形状与 theta 相同 (2,)
"""
grad = (X @ theta - y.flatten()) @ X
regterm = l * theta
regterm[0] = 0
return (grad + regterm) / len(X)
# # 使用初始化为 [1; 1] 的 theta,你应该期望看到一个梯度为 [-15.303016; 598.250744](lambda=1)
print(gradientReg(theta, X, y, 1))
# 1.4 Fitting linear regression 拟合线性回归
def trainLinearReg(X, y, l):
theta = np.zeros(X.shape[1])
res = opt.minimize(fun=costReg, x0=theta, args=(X, y, l), method='TNC', jac=gradientReg)
return res.x
fit_theta = trainLinearReg(X, y, 0)
plotData()
plt.plot(X[:, 1], X @ fit_theta)
# plt.show()
# 这里我们把λ = 0,因为我们现在实现的线性回归只有两个参数,这么低的维度,正则化并没有用。
# 从图中可以看到,拟合最好的这条直线告诉我们这个模型并不适合这个数据。
# 在下一节中,您将实现一个函数来生成学习曲线,它可以帮助您调试学习算法,即使可视化数据不那么容易。
# 2 Bias-variance
# 机器学习中一个重要的概念是偏差(bias)和方差(variance)的权衡。高偏差意味着欠拟合,高方差意味着过拟合。
# 在这部分练习中,您将在学习曲线上绘制训练误差和验证误差,以诊断bias-variance问题。
# 2.1 Learning curves 学习曲线
# 训练样本X从1开始逐渐增加,训练出不同的参数向量θ。接着通过交叉验证样本Xval计算验证误差。
# 1.使用训练集的子集来训练模型,得到不同的theta。
# 2.通过theta计算训练代价和交叉验证代价,切记此时不要使用正则化,将λ = 0
# 3.计算交叉验证代价时记得整个交叉验证集来计算,无需分为子集
def plot_learning_curve(X, y, Xval, yval, l):
"""画出学习曲线,即交叉验证误差和训练误差随样本数量的变化的变化"""
xx = range(1, len(X) + 1) # at least has one example
training_cost, cv_cost = [], []
for i in xx:
res = trainLinearReg(X[:i], y[:i], l)
training_cost_i = costReg(res, X[:i], y[:i], 0)
cv_cost_i = costReg(res, Xval, yval, 0) # 计算交叉验证代价时记得整个交叉验证集来计算,无需分为子集
training_cost.append(training_cost_i)
cv_cost.append(cv_cost_i)
plt.figure(figsize=(8, 5))
plt.plot(xx, training_cost, label='Training cost')
plt.plot(xx, cv_cost, label='Cross validation cost')
plt.legend()
plt.xlabel('Number of training examples')
plt.ylabel('Error')
plt.title('Learning curve for linear regression')
plt.grid(True)
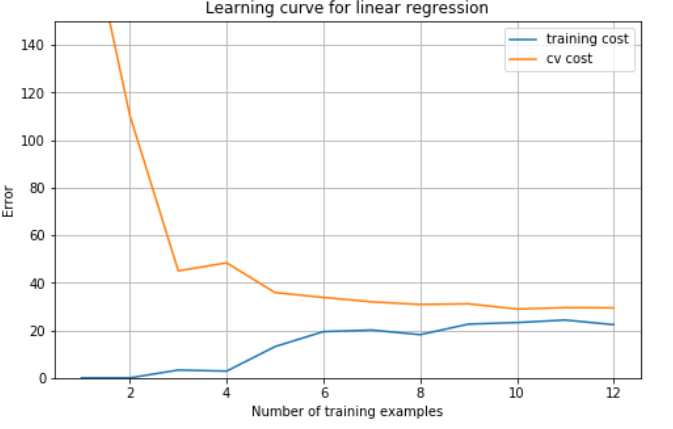
plot_learning_curve(X, y, Xval, yval, 0)
plt.show()
# 从图中看出来,随着样本数量的增加,训练误差和交叉验证误差都很高,这属于高偏差,欠拟合。
# 3 Polynomial regression 多项式回归
# 我们的线性模型对于数据来说太简单了,导致了欠拟合(高偏差)。在这一部分的练习中,您将通过添加更多的特性来解决这个问题。
# 3.1 Learning Polynomial Regression
# 数据预处理
# 1.X,Xval,Xtest都需要添加多项式特征,这里我们选择增加到6次方,因为若选8次方无法达到作业pdf上的效果图,
# 这是因为scipy和octave版本的优化算法不同。
# 2.不要忘了标准化。
def genPolyFeatures(X, power):
"""添加多项式特征
每次在array的最后一列插入第二列的i+2次方(第一列为偏置)
从二次方开始开始插入(因为本身含有一列一次方)
"""
Xpoly = X.copy() # 创建 X 的副本,以避免修改原始数据
for i in range(2, power + 1):
# 将生成的新特征列插入到 Xpoly 的最后一列,axis=1 表示沿着列(横向)插入。
Xpoly = np.insert(Xpoly, Xpoly.shape[1], np.power(Xpoly[:, 1], i), axis=1)
return Xpoly
def get_means_std(X):
"""获取训练集的均值和误差,用来标准化所有数据。"""
means = np.mean(X, axis=0)
# ddof=1是样本标准差,默认=0是总体标准差。因为是子集而不是全部数据集,所以使用样本标准差
stds = np.std(X, axis=0, ddof=1)
return means, stds
def featureNormalize(myX, means, stds):
"""标准化"""
X_norm = myX.copy()
X_norm[:, 1:] = X_norm[:, 1:] - means[1:]
X_norm[:, 1:] = X_norm[:, 1:] / stds[1:]
return X_norm
# 关于归一化,所有数据集应该都用训练集的均值和样本标准差处理。
# 切记。所以要将训练集的均值和样本标准差存储起来,对后面的数据进行处理。
# 获取添加多项式特征以及 标准化之后的数据。
power = 6
train_means, train_stds = get_means_std(genPolyFeatures(X, power))
X_norm = featureNormalize(genPolyFeatures(X, power), train_means, train_stds)
Xval_norm = featureNormalize(genPolyFeatures(Xval, power), train_means, train_stds)
Xtest_norm = featureNormalize(genPolyFeatures(Xtest, power), train_means, train_stds)
def plot_fit(means, stds, l):
"""画出拟合曲线"""
theta = trainLinearReg(X_norm, y, l)
x = np.linspace(-75, 55, 50) # 生成从 -75 到 55 之间的 50 个均匀分布的点
xmat = x.reshape(-1, 1)
xmat = np.insert(xmat, 0, 1, axis=1)
Xmat = genPolyFeatures(xmat, power)
Xmat_norm = featureNormalize(Xmat, means, stds)
plotData()
plt.plot(x, Xmat_norm @ theta, 'b--')
plot_fit(train_means, train_stds, 0)
plot_learning_curve(X_norm, y, Xval_norm, yval, 0)
# plt.show()
# 3.2 Adjusting the regularization parameter
# 上图可以看到,λ = 0时,训练误差太小了,明显过拟合了。我们继续调整λ
lambdas = [0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1., 3., 10.]
errors_train, errors_val = [], []
for l in lambdas:
theta = trainLinearReg(X_norm, y, l)
# 记得把lambda = 0 这是因为我们在评估模型在训练集上的性能时,只关心模型在训练集上的表现,而不是正则化效果。
errors_train.append(costReg(theta, X_norm, y, 0))
errors_val.append(costReg(theta, Xval_norm, yval, 0))
plt.figure(figsize=(8, 5))
plt.plot(lambdas, errors_train, label='Train')
plt.plot(lambdas, errors_val, label='Cross Validation')
plt.legend()
plt.xlabel('lambda')
plt.ylabel('Error')
plt.grid(True)
plt.show()
# 可以看到时交叉验证代价最小的是 lambda = 3
l = lambdas[np.argmin(errors_val)] # np.argmin 用于返回数组或列表中最小值的索引位置。
# 3.4 Computing test set error
theta = trainLinearReg(X_norm, y, 3)
print('test cost(l={}) = {}'.format(3, costReg(theta, Xtest_norm, ytest, 0)))
















 浙公网安备 33010602011771号
浙公网安备 33010602011771号