题解：[HAOI2008]下落的圆盘
时空限制：1000ms / 128MB
原题链接：
Description
有n个圆盘从天而降，后面落下的可以盖住前面的。求最后形成的封闭区域的周长。看下面这副图, 所有的红
色线条的总长度即为所求.
Input
第一行为1个整数n,n<=1000
接下来n行每行3个实数,ri,xi,yi,表示下落时第i个圆盘的半径和圆心坐标.
Output
最后的周长，保留三位小数
Sample Input
2
1 0 0
1 1 0
Sample Output
10.472
题解
两页的爆蛋记录（来自蒟蒻的无助）。
orz千古神犇wzp一眼秒题。
这种题一定要耐心地做（初中数学老师一直这么对我说）。
首先，我们来看其简化版：
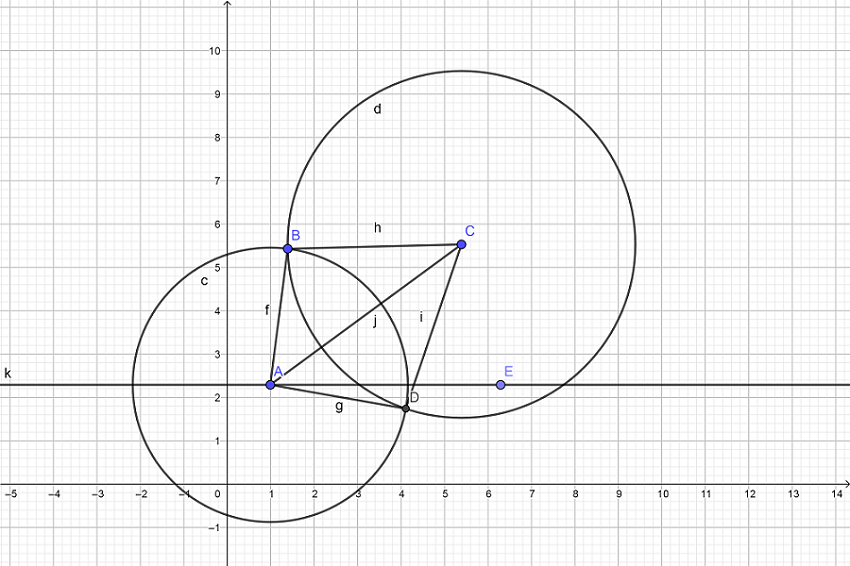
我们把\(\odot B\)覆盖在\(\odot A\)上，我们发现我们需要求出\(\angle A\)的度数。我的方法是连结\(CB,AB,BD,AB\)（如图）。我们发现\(\triangle ABC\cong\triangle ABD\)，又在\(\triangle ABC\)中，由余弦定理得：\(\cos A=\frac{{AC}^2 + {AB}^2 - BC^2}{2\times AB \times AC}\)于是我们就得到了\(\angle A\)。
恭喜你过了样例。
double dist = get_dist(A, B);
if(dist > A.r+B.r || A.r + dist < B.r)
return;
if(dist + B.r < A.r)//完全被覆盖
{
gaif = true;//标记直接跳出
return;
}
double alpha = acos((sqr(B.r)+sqr(dist)-sqr(A.r))/(B.r*dist*2.));
那么如果有多个圆呢？
我们发现，对于\(\odot A\)来说，\(EF\)被覆盖了两次，但我们之能减一次。于是我们就想到了：对于每个圆，枚举盖在其上面的圆，算出每个覆盖“线段”的左右端点，然后进行一次线段覆盖将其合并。最后，我们只要算出没有被覆盖到的线段长度即可。
我们用极角来表示圆上点的位置，这样我们就可以进行线段覆盖操作了。
如图，\(AE\)平行\(x\)轴，我们以算出\(AC\)的斜率，加个\(\arctan\)即可求出\(\angle CAE\)，然后\(\angle EAD\)、\(\angle BAE\)均可求出。
于是理论上的问题就全部解决了。
对于极角还有一个小细节：
由于我们在线段求并时只容许有\(1\)到\(2\pi\)的弧度，因此，对于两个“交点”\(l,r\)，我们需要作出以下特判：
- \(l<0\)且\(r<0\)时，我们要把\(l\)与\(r\)均加上\(2\pi\)；
- \(l<0\)且\(r>0\)时，我们插入\([l+2\pi,2\pi],[0,r]\)两段；
- \(l<2\pi\)且\(r>2\pi\)时，我们插入\([l,2\pi],[0,r-2\pi]\)两段。
具体代码实现如下：
//const double pi2 = 2*pi
if(jiao1 < 0 && jiao2 < 0)//这句话花了我一页的提交
{
jiao1 += pi2, jiao2 += pi2;
}
if(jiao1 >= 0 && jiao2 <= pi2)
cha(jiao1, jiao2);
else
{
if(jiao1 < 0)
{
cha(jiao1+pi2, pi2);
cha(0, jiao2);
}
else
{
cha(jiao1, pi2);
cha(0, jiao2-pi2);
}
}
整体代码
//代码有些冗长，大佬勿喷
//蒟蒻无毒，请放心食用
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 10005;
const double pi = 3.1415926535897932;
const double pi2 = 2*pi;
struct Point
{
double x, y;
};
inline double sqr(double x)
{
return x*x;
}
inline double get_dist(Point x, Point y)
{
return sqrt(sqr(x.x-y.x) + sqr(x.y-y.y));
}
struct Circle
{
Point O;
double r;
} c[maxn];
inline double get_dist(Circle x, Circle y)
{
return get_dist(x.O, y.O);
}
int n;
struct Fugai
{
double l, r;
inline bool operator < (const Fugai& other) const
{
return l < other.l;
}
} fugai[maxn];
int nown;
inline void cha(double l, double r)
{
fugai[++nown] = (Fugai)
{
l, r
};
}
bool gaif = false;//gaif = true表示该圆盘被上面的大圆盘完全覆盖
inline void jiao(Circle A, Circle B)
{
double dist = get_dist(A, B);
if(dist > A.r+B.r || A.r + dist < B.r)//没有任何覆盖
return;
if(dist + B.r < A.r)//如果被一个大圆盘完全覆盖，直接跳出
{
gaif = true;
return;
}
double alpha = acos((sqr(B.r)+sqr(dist)-sqr(A.r))/(B.r*dist*2.));//上图中的角CAD
double beta = atan2(B.O.y-A.O.y, A.O.x-B.O.x);//上图中的角CAE
double jiao1 = beta-alpha;//线段覆盖中的l
double jiao2 = beta+alpha;//线段覆盖中的r
if(jiao1 < 0 && jiao2 < 0)//对极角的一些特判
{
jiao1 += pi2, jiao2 += pi2;
}
if(jiao1 >= 0 && jiao2 <= pi2)
cha(jiao1, jiao2);
else
{
if(jiao1 < 0)
{
cha(jiao1+pi2, pi2);
cha(0, jiao2);
}
else
{
cha(jiao1, pi2);
cha(0, jiao2-pi2);
}
}
}
inline double get_ans()
{
double ans = 0;
sort(fugai+1, fugai+nown+1);
double lastr = fugai[1].l;
for(int i = 1; i <= nown; ++i)
{
if(lastr >= fugai[i].r)
continue;
if(fugai[i].l > lastr)
ans += fugai[i].r - fugai[i].l;
else
ans += fugai[i].r - lastr;
lastr = fugai[i].r;
}
return ans;
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%lf%lf%lf", &c[i].r, &c[i].O.x, &c[i].O.y);
double ans = 0;
for(int i = n; i; --i)
{
nown = 0;
for(int j = n; j > i; --j)//枚举所有该圆盘之后的圆盘
{
jiao(c[j], c[i]);
if(gaif)
break;
}
if(gaif)
gaif = false;
else
ans += (pi2-get_ans())*c[i].r;
nown = 0;
}
printf("%.3f", ans);
return 0;
}
