学习：排序算法
模板题：洛谷P1177【模板】快速排序
此处介绍几种常用的排序方法
1.选择排序
原理
首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
过程
时间复杂度
- 最坏时间复杂度 O(n2)
- 最优时间复杂度 O(n2)
- 平均时间复杂度 O(n2)
伪代码
function sort(array,length)
{
var max
while(length!=0)
{
max=0
for(i from 1 to length-1)
if(array[i]>array[max])
max=i
swap(array[length-1],array[max])
--lengh
}
}
2.冒泡排序
原理
重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法描述
冒泡排序算法的运作如下：
过程
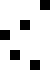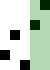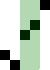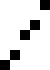
时间复杂度
- 最坏时间复杂度 O(n2)
- 最优时间复杂度 O(n)
- 平均时间复杂度 O(n2)
伪代码
function sort (array, length)
{
var i, j
for(i from 0 to length-1)
{
for(j from 0 to length-1-i)
{
if (array[j] > array[j+1])
{
swap(array[j], array[j+1])
}
}
}
}
模板题
改进
对于有些数据，我们发现，不一定要n-1次才能排完。例如1 5 2 3 4 6，我们发现只需一趟排序就可以将整个序列排完，于是，我们可以设置一个布尔变量，判断是否有进行交换，如果没有交换，说明已经排序完成，进而减少几趟排序。
伪代码
function sort(array,length)
{
bool ok=true //判断是否有交换。
for(i from length-1 downto 0)
{
max=0
for(j from 0 to i)
{
if(array[j]>array[j+1])
{
swap(a[j],a[j+1])
ok=false
}
if(ok)
break //没有交换说明已经排完，直接退出。
}
}
}
3.插入排序
原理
插入排序的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
算法描述
- 从第一个元素开始，该元素可以认为已经被排序
- 取出下一个元素，在已经排序的元素序列中从后向前扫描
- 如果该元素（已排序）大于新元素，将该元素移到下一位置
- 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
过程
时间复杂度
- 最坏时间复杂度 O(n2)
- 最优时间复杂度 O(n)
- 平均时间复杂度 O(n2)
伪代码
function sort(arr, len)
{
var temp
for (i from 1 to len-1)
{
temp = arr[i]
for (j from i downto 1)
{
arr[j] = arr[j-1]
if(arr[j-1] > temp)
{
break
}
}
arr[j] = temp
}
}
4.快速排序
简介
快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），简称快排，一种排序算法，最早由东尼·霍尔提出。在平均状况下，排序\(n\)个项目要\(n\log n\)次比较。在最坏状况下则需要\(n^{2}\)次比较，但这种状况并不常见。事实上，快速排序\(O(n\log n)\)通常明显比其他算法更快，因为它的内部循环可以在大部分的架构上很有效率地达成。
时间复杂度
- 最坏时间复杂度 O(n2)
- 最优时间复杂度 O(nlogn)
- 平均时间复杂度 O(nlogn)
算法
快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为两个子序列（sub-lists）。
步骤为：
- 从数列中挑出一个元素，称为"基准"（pivot），
- 重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任何一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
- 递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。
- 递归到最底部时，数列的大小是零或一，也就是已经排序好了。这个算法一定会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。
演示
改进：原地分区的版本
通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。
假设待排序的序列为\({a[L],a[L+1],a[L+2],……,a[R]}\)，首先任意选取一个记录（通常可选中间一个记作为枢轴或支点），然后重新排列其余记录，将所有关键字小于它的记录都放在左子序列中，所有关键字大于它的记录都放在右子序列中。由此可以将该“支点”记录所在的位置mid作分界线，将序列分割成两个子序列和。这个过程称作一趟快速排序（或一次划分）。
一趟快速排序的具体做法是：附设两个指针i和j，它们的初值分别为L和R，设枢轴记录取mid，则首先从j所指位置起向前搜索找到第一个关键字小于的mid的记录，然后从i所指位置起向后搜索，找到第一个关键字大于mid的记录，将它们互相交换，重复这两步直至i>j为止。
演示
c++代码
inline void sort(int *a,int l,int r)
{
int mid;
int i=l,j=r;
mid=a[(l+r)>>1];//分治。
do
{
while(a[i]<mid)//在左半部分寻找比中间大的数
i++;
while(a[j]>mid)//在右半部分寻找比中间小的数
j--;
if(i<=j)
{
swap(a[i],a[j]);
i++,j--;//继续找。
}
}
while(i<=j);
if(l<j)//若未到边界，继续找。
sort(a,l,j);
if(i<r)
sort(a,i,r);
}
比赛时手打快排？不存在的……
#include <cstdio>
#include <algorithm>
using namespace std;
int a[100005];
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;scanf("%d",a+(i++)));
sort(a,a+n);
printf("%d",a[0]);
for(int i=1;i<n;printf(" %d",*(a+(i++))));
puts("");
return 0;
}
5.归并排序
简介
归并排序（英语：Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法，效率为\(O(n\log n)\)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法的一个非常典型的应用，且各层分治递归可以同时进行。
时间复杂度
- 最坏时间复杂度 O(nlogn)
- 最优时间复杂度 O(n)
- 平均时间复杂度 O(nlogn)
算法描述
- 把原数组分拆为\(n\)个长度为\(1\)的子数组。
- 将长度为\(1\)的子数组两两归并为\(n/2\)个长度为\(2\)的子数组，并使每个子数组有序。
- 重复步骤 2 直至所有子数组归并为长度为\(n\)的有序数组为止。
演示
c++代码
void sort(int l,int r)
{
if(l==r)//若只有一个数字，则无需排序
return;
int mid=(l+r)>>1;
sort(l,mid);
sort(mid+1,r);//分治
int i=l,j=mid+1,k=l;
while(i<=mid&&j<=r)//开始合并
if(a[i]<=a[j])
t[k++]=a[i++];
else
t[k++]=a[j++];
while(i<=mid)//复制左边子序列剩余
t[k++]=a[i++];
while(j<=r)//复制右边子序列剩余
t[k++]=a[j++];
for(int i=l;i<=r;++i)//复制回来
a[i]=t[i];
}
