js数值类型
js数值类型--number
更详细的参考资料
中文wiki-IEEE754
中文wiki-IEEE754(免FQ版)
js数值类型的存储形式
JavaScript 内部,所有数字都是以64位浮点数形式储存,即使整数也是如此.
- 什么是浮点数?
利用科学计数法来表达实数(Number),即用一个尾数/小数部分(Fraction),一个基数(Base,通常为2),一个指数(Exponent)以及一个表示正负的符号(Sign)来表达实数。尾数有时也称为有效数字(Significand)
浮点数表示公式: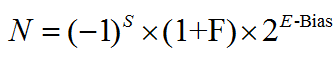
其存储结构为:
各部分说明: - 符号域Sign:决定数值的正负
- 指数域Exponent:决定数值的小数点位置
- 指数偏移值(修正值)Bias:为了使指数域区分正负(小数点既可右移,也可左移),而在存储时默认减掉的一个值,64位浮点数该值为1023=(1/2)*2指数域位数-1=210-1(因为初始值从0开始,所以减去1)
- 小数域/有效数字域Fraction:小数点之后的有效数字(未与指数域相乘之前)
但是,同一个数值,由于指数域的取值不同会有不同的表示方法,例:12.34=1.234×101=0.1234×102.为了提高数据的表示精度同时保证数据表示的唯一性,需要对浮点数做规格化处理。
在计算机内,对非0值的浮点数,要求尾数的绝对值必须大于基数的倒数,即|F|≥1/B.对于二进制来说,就是:要求尾数域的最高有效位应为1,把不满足这一表示要求的尾数,变成满足这一要求的尾数的操作过程,叫作浮点数的规格化处理,通过尾数移位和修改阶码实现规格化要求。
js数值的范围与精度(有效数位数)
一般情况下(normalized,0< E< 2047)
js数值类型表示整数的范围
- js数值中,整数都可以被精确存储;而很多小数的存储会有误差(见后续章节)
- 由以上js数值的存储结构:有效数字有53位(一个隐含位),也就是说,绝对值小于2的53次方的整数,即-2^53 到 2^53的整数,都可以精确表示.
- 注:js能精确表示的最大数值是253 ,但可以表示的最大数值不是 253.
特殊情况下
- 情况1:denormalized(非规约形式的浮点数: 有效数字隐含位,也就是浮点数整数部分=0,E=0,0<F<1)
此种情况下,有效数字的隐含位(小数点之前)由1变为0且计算公式变为:±0.F×2(-1022)
[注意:denormalized下,E取0,但指数域不是-1023而是-1022.]
- 情况2:零值(E=0,F=0)
由于符号位S是独立存储的,所以由+0和-0之分. - 情况3:infinity无穷大(E=2047,F=0)
同零值,也有+∞和-∞之分. - 情况4:NaN(not a number)(E=2047,F>0)
注:
- 正向溢出(overflow):一个数>=2^1024,返回infinity
- 反向溢出(underflow):一个数小于2^(-1075)(指数部分最小的-1023加上52位小数部分),返回0.
js中能表示的最大值与最小值(绝对值)

-
最大值Number.MAX_VALUE
如上图,最大值应该是仅次于infinity的值,也就是E=2046,F为全1时的值,因此:
Number.MAX_VALUE=1×(21023)×1.1....1=1×2(1023-52)×11....1B=2^(1023-52)×9007199254740991≈1.7976931348623157e+308 -
最小值Number.MIN_VALUE
最小值应该是指数域E=0,而小数域F仅有最低位为1时的值.属于denormalized,因此根据其公式:
Number.MIN_VALUE=1×2(-1022)×2(-52)≈5e-324
js中十进制小数的存储与运算不准确的问题
知识回顾:十进制转二进制
-
正整数部分:除二取余,倒序排列
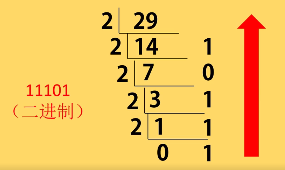
-
小数部分:乘二取整,正序排列

十进制小数转二进制小数的问题
一些小数,例如0.1,0.2,0.3,0.4等,在转换为二进制时,其位数是无穷的,而我们用于存储的空间只有52位,所以要进行舍入,那么就会产生误差.
举例 0.1+0.2===0.3为false
-
首先,我们用在线任意进制转换器对0.1,0.2进行十进制到二进制转换:
0.1D=0.00011001100110011001100110011001100110011001100110011010B
0.2D=0.00110011001100110011001100110011001100110011001100110100B
0.3D=0.010011001100110011001100110011B
(注意:上述三个十进制小数对应的二进制数位数本身是无穷,我们对此作了第52位的舍入,即截取前52位,并在第52位上加1) -
接着我们对上述0.1和0.2两行二进制数进行二进制加法运算,得到如下结果:
0.01001100110011001100110011001100110011001100110011001110 -
再借由在线任意进制转换器将结果转换回十进制,得到结果为:
0.3000000000000000444089209850062616169452667236328125.
同时,我们运行js代码:
alert((0.1+0.2));
得到结果为:

总结:
我们在键盘输入一个十进制数值后,js会将之进行十进制到二进制的转换并存储,在此过程中产生了误差,等到我们再次使用这个值的时候,它已经不是原来正确的值了.
解决办法(简单但不严谨):
将要计算的小数转换为整数进行计算,计算完毕后再转换回小数(只适用于四则运算).
数值的表示方法
-
字面量直接表示:
- 十进制:35
- 二进制:10010B或者前缀0b(数字0,字母b)
- 八进制:前缀0(数字0).如果有前缀0,其后又有8,9视为十进制
- 十六进制:前缀0x(数字0,字母x/X)
-
科学计数法:(以下两种情况,js自动转换为科学计数法)
- 小数点前数字多于21位
- 小数点后的零多于5个
关于js中的NaN
- NaN不是数据类型,只是基本类型number里的特殊值
- NaN不等于任何值,包括它本身
- NaN转换为布尔值为false
- 用isNaN(x)方法判断一个值是否是NaN(注意:isNaN只针对数值,传入非数值参数可能会出现问题)
与数值有关的全局方法
-
parseInt(str):将字符串转换为整数
转换说明: -
自动过滤前导的空格
-
如果参数不是字符串,会先将其转换为字符串,再进行操作
-
转换过程是一个一个字符逐个进行,遇到不能转换为数字的字符,返回已经转换的部分;如果第一个字符都不能转换,返回NaN
-
字符串以0开头,按十进制转换;以0x或0X开头,按16进制转换
-
遇到自动转换为科学计数法的数字字符串,parseInt()会将其科学计数法表示的形式作为字符串进行转换,从而产生古怪的结果.
第二参数:
-
parseInt(str)还可以接受第二个参数(2-36),指明被解析值的进制,返回该值对应的十进制数;
-
若第二个数值超出2-36范围,返回NaN
-
第二个数值为0,null,undefined,直接忽略
-
如果第二个参数为非数值,先将之转换为数值,再按前两个情况判断和操作
-
如果第一个参数包含对于指定进制无意义的字符,只返回可转换的部分(若最高位无法转换,返回NaN)
-
parseFloat(str):将字符串转换为浮点数
转换说明: -
自动过滤字符串前导空格
-
如果参数不是字符串或者字符串第一个字符不能转换,返回NaN(此处与parseInt不同)
-
转换过程是一个一个字符逐个进行,遇到不能转换为浮点数的字符,返回已经转换的部分
-
会将空字符转换为NaN
-
isNaN(x):判断一个值是否为NaN
转换说明: -
isNaN()只对数值精准有效,如果传入非数值,会先将其转为数值,再进行判断:
isNaN('123')==false;isNaN('abc')==true;isNaN(Array)/isNaN(Object)==true -
但是,对于空数组和只有一个数值成员的数组,null,isNaN()返回false;不过,对于空对象{},返回true
-
因此,判断NaN应该利用它是唯一一个"不等于自身的值"的特性来实现
-
isFinite():判断某个值是否为正常的数值
-
isFinite()只对数值精准有效,如果传入非数值,会先将其转为数值,再进行判断.
-
但是,对于空数组和只有一个数值成员的数组,null,isNaN()返回true;不过,对于空对象{},返回false
-
对于Infinite,-Infinite,NaN,undefined返回false
欢迎转载,转载请注明出处


