【第二章】利用用户行为数据

基于用户行为分析的推荐算法是个性化推荐系统的重要算法，学术界一般将这种类型的算法称为协同过滤算法。顾名思义，协同过滤就是指用户可以齐心协力，通过不断地和网站互动，使自己的推荐列表能够不断过滤掉自己不感兴趣的物品，从而越来越满足自己的需求。

2.1 用户行为数据简介

一般来说，不同的数据集包含不同的行为，目前比较有代表性的数据集有下面几个。

无上下文信息的隐性反馈数据集每一条行为记录仅仅包含用户ID和物品ID。Book-Crossing就是这种类型的数据集。
无上下文信息的显性反馈数据集每一条记录包含用户ID、物品ID和用户对物品的评分。
有上下文信息的隐性反馈数据集每一条记录包含用户ID、物品ID和用户对物品产生行为的时间戳。Last.fm数据集就是这种类型的数据集。
有上下文信息的显性反馈数据集每一条记录包含用户ID、物品ID、用户对物品的评分和评分行为发生的时间戳。Netflix Prize提供的就是这种数据集。

2.2 用户行为分析

2.2.1 用户活跃度和物品流行度的分布

很多关于互联网数据的研究发现，互联网上的很多数据分布都满足一种称为Power Law的分布，这个分布在互联网领域也称长尾分布:

\[f(x) = \alpha x^k \]

用户行为数据也蕴含着这种规律。令fu(k)为对k个物品产生过行为的用户数，令fi(k)为被k个用户产生过行为的物品数。那么，fu(k)和fi (k)都满足长尾分布。也就是说:

\[f_i(k) = \alpha _ik^{\beta_i} \]

\[f_u(k) = \alpha _uk^{\beta_u} \]

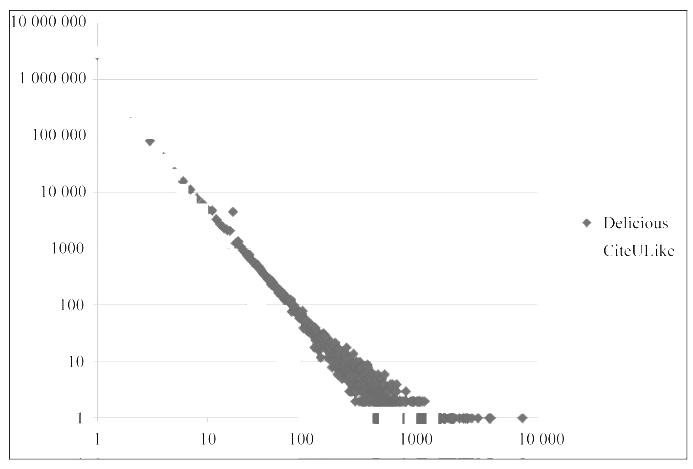
物品流行度的长尾分布

物品流行度的长尾分布 **这个定理说明了说明大部分物品的流行度和用户活跃度较低**

2.2 用户活跃度和物品流行度的关系

一般认为，新用户倾向于浏览热门的物品，因为他们对网站还不熟悉，只能点击首页的热门物品，而老用户会逐渐开始浏览冷门的物品。用户越活跃，越倾向于浏览冷门的物品
协同过滤算法一般有两种：

基于用户的协同过滤算法这种算法给用户推荐和他兴趣相似的其他用户喜欢的物品
基于物品的协同过滤算法这种算法给用户推荐和他之前喜欢的物品相似的物品。

2.3 实验设计和算法评测

协同过滤算法的离线实验一般如下设计。

首先，将用户行为数据集按照均匀分布随机分成M份（本章取M=8），挑选一份作为测试集，将剩下的M-1份作为训练集。
然后在训练集上建立用户兴趣模型，并在测试集上对用户行为进行预测，统计出相应的评测指标。
为了保证评测指标并不是过拟合的结果，需要进行M次实验，并且每次都使用不同的测试集。
然后将M次实验测出的评测指标的平均值作为最终的评测指标

2.3.3 评测指标

召回率描述有多少比例的用户——物品评分记录包含在最终的推荐列表中
准确率描述最终的推荐列表中有多少比例是发生过的用户——物品评分记录。
覆盖率最简单定义：最终的推荐列表中包含多大比例的物品。如果所有的物品都被推荐给至少一个用户，那么覆盖率就是100%
新颖度用推荐列表中物品的平均流行度度量推荐结果的新颖度。在计算平均流行度时对每个物品的流行度取对数，这是因为物品的流行度分布满足长尾分布，在取对数后，流行度的平均值更加稳定

2.4 基于领域的算法

2.4.1 基于用户的协同过滤（UserCF）

在一个在线个性化推荐系统中，当一个用户A需要个性化推荐时，可以先找到和他有相似兴趣的其他用户，然后把那些用户喜欢的、而用户A没有听说过的物品推荐给A。

基于用户的协同过滤算法主要分为两步。

找到和目标用户兴趣相似的用户集合。
找到这个集合中的用户喜欢的，且目标用户没有听说过的物品推荐给目标用户。

兴趣相似度计算：
给定用户u和用户v，令N(u)表示用户u曾经有过正反馈的物品集合，令N(v)为用户v曾经有过正反馈的物品集合。那么，我们可以通过如下的Jaccard公式简单地计算u和v的兴趣相似度：

\[{|N(u) \cap N(v)|} \over {|N(u) \cup N(v)|} \]

或者通过余弦相似度计算：

\[{|N(u) \cap N(v)|} \over \sqrt{|N(u)||N(v)|} \]

缺点：这种方法的时间复杂度是，这在用户数很大时非常耗时。事实上，很多用户相互之间并没有对同样的物品产生过行为，即很多时候。上面的算法将很多时间浪费在了计算这种用户之间的相似度上。

解决方法——用户倒排表
为此，可以首先建立物品到用户的倒排表，对于每个物品都保存对该物品产生过行为的用户列表。令稀疏矩阵。那么，假设用户u和用户v同时属于倒排表中K个物品对应的用户列表，就有C[u][v]=K。从而，可以扫描倒排表中每个物品对应的用户列表，将用户列表中的两两用户对应的C[u][v]加1，最终就可以得到所有用户之间不为0的C[u][v]
得到用户之间的兴趣相似度后，UserCF算法会给用户推荐和他兴趣最相似的K个用户喜欢的物品。如下的公式度量了UserCF算法中用户u对物品i的感兴趣程度：

\[p(u, i) = \sum_{v \in S(u, K) \cap N(i)}{w_{uv}r_{vi}} \]

其中，\(S (u , K )\)包含和用户\(u\)兴趣最接近的K 个用户，\(N (i )\)是对物品\(i\) 有过行为的用户集合，\(w_{uv}\) 是用户\(u\)和用户v的兴趣相似度，\(r_{vi}\) 代表用户v对物品i的兴趣，因为使用的是单一行为的隐反馈数据，所以所有的\(r_{vi}\)=1

UserCF的代码：

        def Recommend(user, train, W):
            rank = dict()
            interacted_items = train[user]
            for v, wuv in sorted(W[u].items, key=itemgetter(1), \
                reverse=True)[0:K]:
                for i, rvi in train[v].items:
                    if i in interacted_items:
                          #we should filter items user interacted before
                          continue
                    rank[i] += wuv ＊ rvi
            return rank

结果分析

MostPopular算法的准确率和召回率远远高于Random算法，但它的覆盖率非常低，结果都非常热门。可见，Random算法的准确率和召回率很低，但覆盖度很高，结果平均流行度很低。

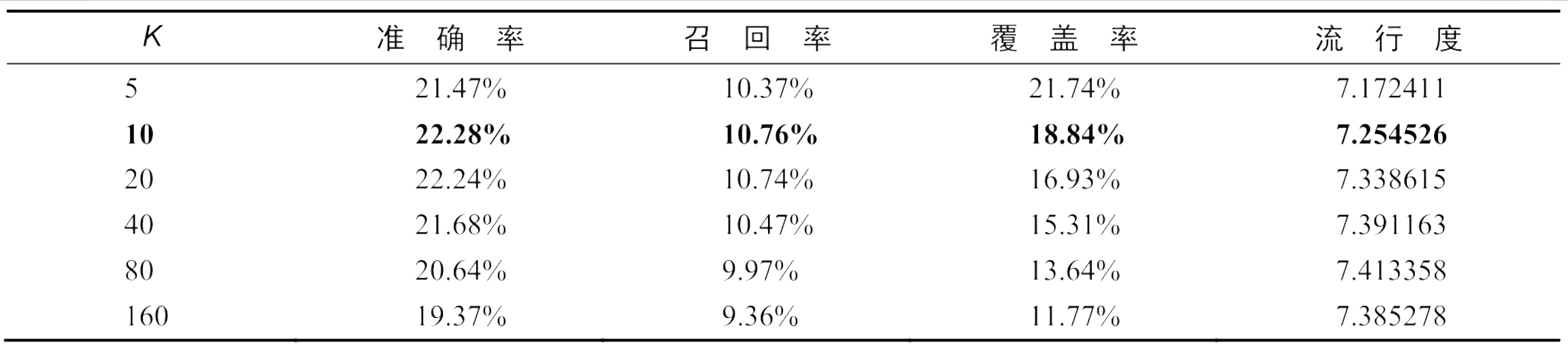
准确率和召回率因此选择合适的K 对于获得高的推荐系统精度比较重要。当然，推荐结果的精度对K 也不是特别敏感，只要选在一定的区域内，就可以获得不错的精度。
流行度K 越大则UserCF推荐结果就越热门。这是因为K 决定了UserCF在给你做推荐时参考多少和你兴趣相似的其他用户的兴趣，那么如果K 越大，参考的人越多，结果就越来越趋近于全局热门的物品
覆盖率K越大覆盖率越低

用户相似计算的改进

以图书为例，如果两个用户都曾经买过《新华字典》，这丝毫不能说明他们兴趣相似，因为绝大多数中国人小时候都买过《新华字典》。但如果两个用户都买过《数据挖掘导论》，那可以认为他们的兴趣比较相似，因为只有研究数据挖掘的人才会买这本书。换句话说，两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度

\[w_{uv} = \frac{\sum_{i \in N(u)\cap N(v)} {\frac{1}{log(1+|N(i)|)}}}{\sqrt {|N(u)||N(v)|}} \]

可以看到，该公式通过惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响
相比我们后面要讨论的基于物品的协同过滤算法（ItemCF）, UserCF在目前的实际应用中使用并不多。

2.4.2 基于物品的协同过滤（ItemCF）

基于物品的协同过滤算法（简称ItemCF）给用户推荐那些和他们之前喜欢的物品相似的物品。比如，该算法会因为你购买过《数据挖掘导论》而给你推荐《机器学习》。不过，ItemCF算法并不利用物品的内容属性计算物品之间的相似度，它主要通过分析用户的行为记录计算物品之间的相似度。该算法认为，物品A和物品B具有很大的相似度是因为喜欢物品A的用户大都也喜欢物品B。

基于物品的协同过滤算法主要分为两步。

计算物品之间的相似度。
根据物品的相似度和用户的历史行为给用户生成

\[w_{ij} = \frac{|N(i) \cap N(j)|} {\sqrt{|N(i)||N(j)|}} \]

分母|N(i)|是喜欢物品i的用户数，而分子N(i)∩N( j) 是同时喜欢物品i和物品j的用户数。这个公式惩罚了物品j的权重，因此减轻了热门物品会和很多物品相似的可能性。在协同过滤中两个物品产生相似度是因为它们共同被很多用户喜欢，也就是说每个用户都可以通过他们的历史兴趣列表给物品“贡献”相似度

在得到物品之间的相似度后，ItemCF通过如下公式计算用户u对一个物品j的兴趣：

\[p_{uj} = \sum_{i \in N(u) \cap S(j, K)}{w_{ji}r_{ui}} \]

这里N(u)是用户喜欢的物品的集合，S(j, K)是和物品j最相似的K个物品的集合，\(w_{ji}\)是物品j和i的相似度，rui是用户u对物品i的兴趣。（对于隐反馈数据集，如果用户u对物品i有过行为，即可令\(r_{ui}=1\)

ItemCF的代码：

        def Recommendation(train, user_id, W, K):
            rank = dict()
            ru = train[user_id]
            for i, pi in ru.items():
                for j, wj in sorted(W[i].items(), /
                                    key=itemgetter(1), reverse=True)[0:K]:
                    if j in ru:
                          continue
                    rank[j] += pi ＊ wj
            return rank

结果分析

准确率和召回率 可以看到ItemCF推荐结果的精度也是不和K 成正相关或者负相关的，因此选择合适的K 对获得最高精度是非常重要的。。
流行度不和K完全正相关
覆盖率K越大覆盖率越低

用户活跃度对物品相似度的影响

每个用户对相似度的共享不应相同：
举例：书店老板所购买书对两两相似度的贡献应该远远小于一个只买了十几自己喜欢的书的文学青年。
所以，对于很多过于活跃的用户，比如上面那位了当当网80%图书的用户，为了避免相似度矩阵于稠密，我们在实际计算中一般直接忽略他的兴趣列表，而不将其纳入到相似度计算的数据集中

物品相似度归一化

Karypis在研究中发现如果将ItemCF的相似度矩阵按最大值归一化，可以提高推荐的准确率。其研究表明，如果已经得到了物品相似度矩阵w，那么可以用如下公式得到归一化之后的相似度矩阵w＇

\[w_{ij} = \frac{w_{ij}}{max_{j}w_{ij}} \]

原因分析：

其实，归一化的好处不仅仅在于增加推荐的准确度，它还可以提高推荐的覆盖率和多样性。一般来说，物品总是属于很多不同的类，每一类中的物品联系比较紧密。举一个例子，假设在一个电影网站中，有两种电影——纪录片和动画片。那么，ItemCF算出来的相似度一般是纪录片和纪录片的相似度或者动画片和动画片的相似度大于纪录片和动画片的相似度。但是纪录片之间的相似度和动画片之间的相似度却不一定相同。假设物品分为两类——A和B, A类物品之间的相似度为0.5, B类物品之间的相似度为0.6，而A类物品和B类物品之间的相似度是0.2。在这种情况下，如果一个用户喜欢了5个A类物品和5个B类物品，用ItemCF给他进行推荐，推荐的就都是B类物品，因为B类物品之间的相似度大。但如果归一化之后，A类物品之间的相似度变成了1, B类物品之间的相似度也是1，那么这种情况下，用户如果喜欢5个A类物品和5个B类物品，那么他的推荐列表中A类物品和B类物品的数目也应该是大致相等的。从这个例子可以看出，相似度的归一化可以提高推荐的多样性。

一般来说，热门的类其类内物品相似度一般比较大。如果不进行归一化，就会推荐比较热门的类里面的物品，而这些物品也是比较热门的。因此，推荐的覆盖率就比较低。相反，如果进行相似度的归一化，则可以提高推荐系统的覆盖率。

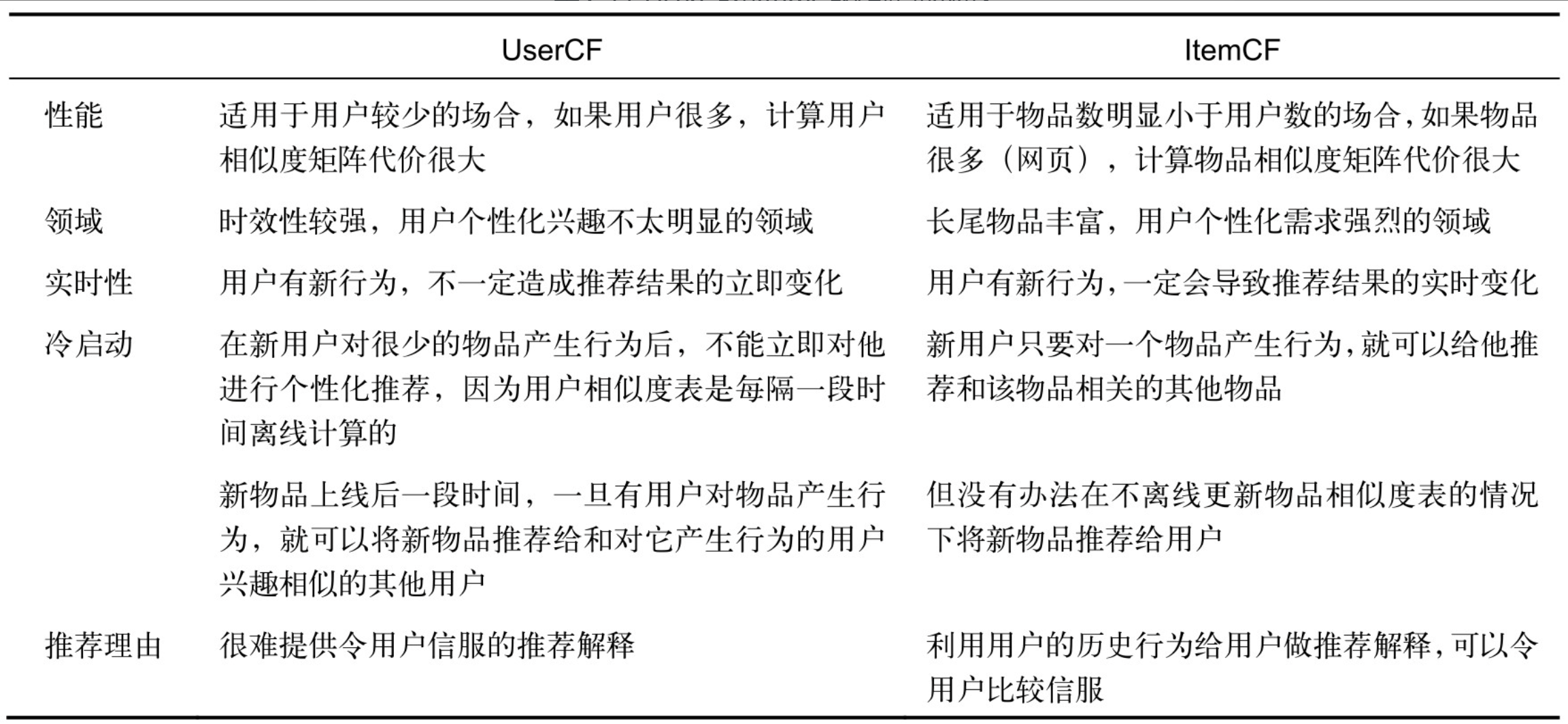
2.4.3 UserCF和ItemCF的综合比较

为什么新闻网站使用UserCF，而亚马逊网使用ItemCF呢？

UserCF的推荐结果着重于反映和用户兴趣相似的小群体的热点，而ItemCF的推荐结果着重于维系用户的历史兴趣。
相似度矩阵的更新：UserCF适合用于新闻推荐的另一个原因是从技术角度考量的。因为作为一种物品，新闻的更新非常快，每时每刻都有新内容出现，而ItemCF需要维护一张物品相关度的表，如果物品更新很快，那么这张表也需要很快更新，这在技术上很难实现。绝大多数物品相关度表都只能做到一天一次更新，这在新闻领域是不可以接受的。
存储：从技术上考虑，UserCF需要维护一个用户相似度的矩阵，而ItemCF需要维护一个物品相似度矩阵。从存储的角度说，如果用户很多，那么维护用户兴趣相似度矩阵需要很大的空间，同理，如果物品很多，那么维护物品相似度矩阵代价较大。实际的互联网中，用户数目往往非常庞大，而在图书、电子商务网站中，物品的数目则是比较少的。此外，物品的相似度相对于用户的兴趣一般比较稳定，因此使用ItemCF是比较好的选择。

哈利波特问题

亚马逊网的研究人员在设计ItemCF算法之初发现ItemCF算法计算出的图书相关表存在一个问题，就是很多书都和《哈利波特》相关。[插图]也就是说，购买任何一本书的人似乎都会购买《哈利波特》。后来他们研究发现，主要是因为《哈利波特》太热门了，确实是购买任何一本书的人几乎都会购买它。

两个不同领域的最热门物品之间往往具有比较高的相似度。这个时候，仅仅靠用户行为数据是不能解决这个问题的，因为用户的行为表示这种物品之间应该相似度很高。此时，我们只能依靠引入物品的内容数据解决这个问题，比如对不同领域的物品降低权重等。这些就不是协同过滤讨论的范畴了。

2.5 隐语义模型（Latent Factor Model）

隐语义模型是最近几年推荐系统领域最为热门的研究话题，它的核心思想是通过隐含特征(latent factor)联系用户兴趣和物品。

\[Preference(u, i) = r_{ui} = p_{u}^{T}q_i = \sum_{f = 1}^{F}{p_{u, k}q_{i, k}} \]

这个公式中pu,k 和qi,k 是模型的参数，其中pu,k 度量了用户u的兴趣和第k个隐类的关系，而qi,k度量了第k个隐类和物品i之间的关系

要计算这两个参数，需要一个训练集，对于每个用户u，训练集里都包含了用户u喜欢的物品和不感兴趣的物品，通过学习这个数据集，就可以获得上面的模型参数。

LFM在显性反馈数据（也就是评分数据）上解决评分预测问题并达到了很好的精度。不过本章主要讨论的是隐性反馈数据集，对负样本采样时应该遵循以下原则。

对每个用户，要保证正负样本的平衡（数目相似）。
对每个用户采样负样本时，要选取那些很热门，而用户却没有行为的物品。

经过采样，可以得到一个用户—物品集\(K=\{( u, i)\}\)，其中如果(u, i)是正样本，则有\(r_{ui}=1\)，否则有\(r_{ui}=0\)。然后，需要优化如下的损失函数来找到最合适的参数p和q：

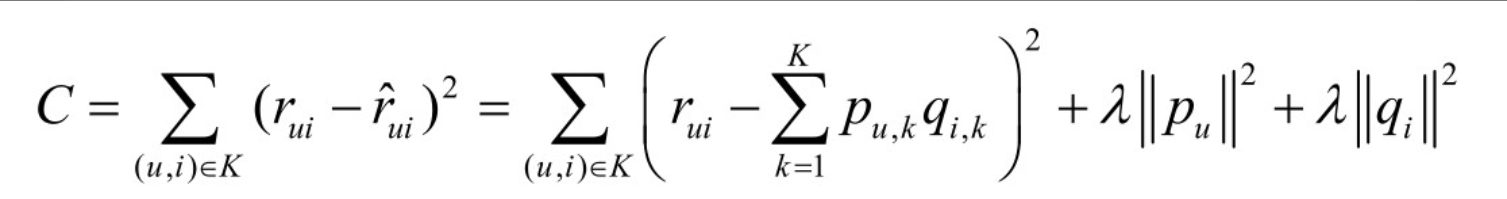
\(\lambda ||p_{u}^{2}|| + \lambda ||q_{i}^2||\)是用来防止过拟合的正则化项，\(\lambda\)可以通过实验获得。要最小化上面的损失函数，可以利用随机梯度下降法(SGD)

通过实验对比了LFM在TopN推荐中的性能。在LFM中，重要的参数有4个：

隐特征的个数F；
学习速率alpha；
正则化参数lambda；
负样本/正样本比例 ratio。
通过实验发现，ratio参数对LFM的性能影响最大。随着负样本数目的增加，覆盖率不断降低，而推荐结果的流行度不断增加，说明ratio参数控制了推荐算法发掘长尾的能力

2.5.2 基于LFM的实际系统的例子——雅虎首页

如果用户u单击过链接i，那么就定义(u,i)是正样本，即\(r_{ui} =1\)。如果链接i展示给用户u，但用户u从来没有单击过，那么就定义(u, i)是负样本，即\(r_{ui} =-1\)。然后，雅虎的研究人员利用前文提到的LFM预测用户是否会单击链接

\[\hat{r_{ui}} = p_{u}^{T}q_{i} \]

缺点: LFM模型在实际使用中有一个困难，那就是它很难实现实时的推荐。经典的LFM模型每次训练时都需要扫描所有的用户行为记录，这样才能计算出用户隐类向量（pu）和物品隐类向量（qi）。而且LFM的训练需要在用户行为记录上反复迭代才能获得比较好的性能。因此，LFM的每次训练都很耗时.
然而，新闻推荐中，冷启动问题非常明显。每天都会有大量新的新闻。这些新闻会在很短的时间内获得很多人的关注，但也会在很短的时间内失去用户的关注。因此，它们的生命周期很短，而推荐算法需要在它们短暂的生命周期内就将其推荐给对它们感兴趣的用户。

解决方案：

首先，他们利用新闻链接的内容属性（关键词、类别等）得到链接i的内容特征向量yi。其次，他们会实时地收集用户对链接的行为，并且用这些数据得到链接i的隐特征向量qi。
然后，他们会利用如下公式预测用户u是否会单击链接i：

\[r_{ui} = x_u^T \cdot y_i + p_u^T \cdot q_i \]

中，\(y_i\)是根据物品的内容属性直接生成的，\(x_{uk}\)是用户u对内容特征k的兴趣程度，用户向量\(x_u\)可以根据历史行为记录获得，而且每天只需要计算一次。而\(p_u\)、\(q_i\)是根据实时拿到的用户最近几小时的行为训练LFM获得的。因此，对于一个新加入的物品i，可以通过\(x_u^T \cdot y_i\)估计用户u对物品i的兴趣，然后经过几个小时后，就可以通过\(p_u^T \cdot q_i\)得到更加准确的预测值。

2.5.3 LFM和基于邻域的方法的比较

理论基础：LFM具有比较好的理论基础，它是一种学习方法，通过优化一个设定的指标建立最优的模型。基于邻域的方法更多的是一种基于统计的方法，并没有学习过程。
离线计算的空间复杂度：假设有M 个用户和N 个物品，在计算相关表的过程中，如果是计算是用户相关表，则需要\(O(M *M )\)的空间，而对于物品相关表，则需要\(O(N *N )\)的空间。而LFM在建模过程中，如果是F个隐类，那么它需要的存储空间是\(O(F *(M +N ))\)，这在M和N很大时可以很好地节省离线计算的内存。
离线计算的空间复杂度: 假设有M 个用户、N 个物品、K条用户对物品的行为记录。那么，UserCF计算用户相关表的时间复杂度是\(O(N * (K /N )^2)\)，而ItemCF计算物品相关表的时间复杂度是\(O(M *(K /M )^2)\)。而对于LFM，如果用F个隐类，迭代S 次，那么它的计算复杂度是\(O(K * F * S )\)。那么，如果\(K /N < F *S\)，则代表UserCF的时间复杂度低于LFM，如果\(K /M < F *S\)，则说明ItemCF的时间复杂度低于LFM。在一般情况下，LFM的时间复杂度要稍微高于UserCF和ItemCF，这主要是因为该算法需要多次迭代。但总体上，这两种算法在时间复杂度上没有质的差别。
在线实时推荐：在线实时推荐 UserCF和ItemCF都可以很方便的根据已有的相关表做实时推荐，但是对于LFM，需要遍历整个用户物品对进行模型更新，计算复杂度达\(O(M * N * F)\)，因此LFM不适合用在物品数目非常庞大的系统。如果一定要用，可以先用一个较快的算法先给出一个较小的推荐列表，再用LFM进行重新排名。另一方面，LFM生成一个用户的推荐列表时速度太慢，因此不能在线实时推荐，需要离线的把所有结果实现计算好并存储，因此不能进行在线实时推荐，也就是说，用户产生新的行为后，推荐列表会暂时不变
推荐解释: ItemCF算法支持很好的推荐解释，它可以利用用户的历史行为解释推荐结果。但LFM无法提供这样的解释，它计算出的隐类虽然在语义上确实代表了一类兴趣和物品，却很难用自然语言描述并生成解释展现给用户

2.6 基于图的推荐系统

2.6.1 用户行为数据的二分图表示

令\(G(V , E)\)表示用户物品二分图，其中\(V = V_U∪ V_I\) 由用户顶点集合\(V_U\)和物品顶点集合\(V_I\)组成。对于数据集中每一个二元组\((u, i)\)，图中都有一套对应的边\(e( v_u, v_i)\)，其中\(v_u \in v_u\)是用户u对应的顶点，vi∈VI是物品i对应的顶点。

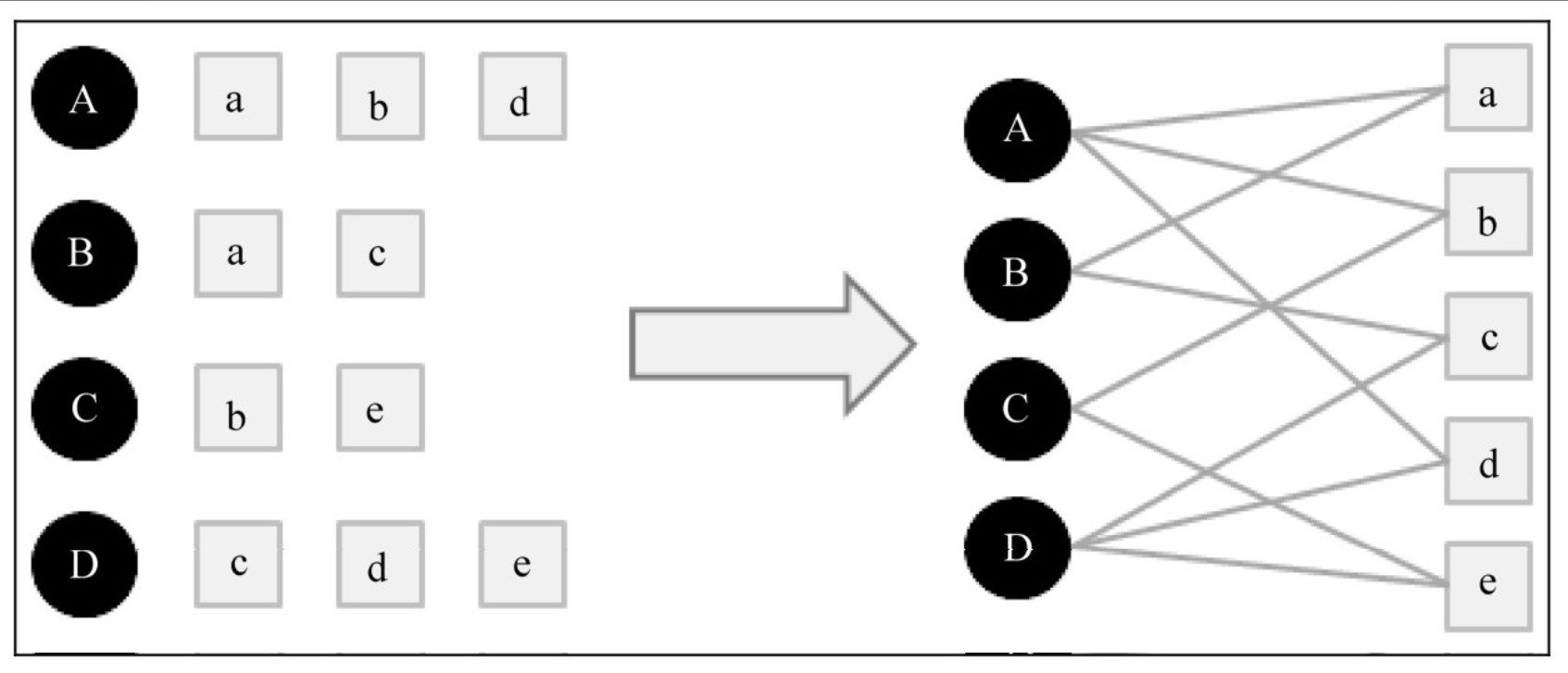
2.6.2 基于图的推荐算法

将用户行为表示为二分图模型后，如果将个性化推荐算法放到二分图模型上，那么给用户u推荐物品的任务就可以转化为度量用户顶点\(v_u\)和与\(v_u\)没有边直接相连的物品节点在图上的相关性，相关性越高的物品在推荐列表中的权重就越高。

度量图中两个顶点之间相关性的方法很多，但一般来说图中顶点的相关性主要取决于下面3个因素：

两个顶点之间的路径数 -> 两个顶点之间有很多路径相连
两个顶点之间路径的长度 -> 连接两个顶点之间的路径长度都比较短
两个顶点之间的路径经过的顶点 -> 连接两个顶点之间的路径不会经过出度比较大的顶点
介绍一种计算相关性的算法——Personal Rank

假设要给用户u进行个性化推荐，可以从用户u对应的节点vu开始在用户物品二分图上进行随机游走。游走到任何一个节点时，

首先按照概率α决定是继续游走，还是停止这次游走并从vu节点开始重新游走。

如果决定继续游走，那么就从当前节点指向的节点中按照均匀分布随机选择一个节点作为游走下次经过的节点。
这样，经过很多次随机游走后，每个物品节点被访问到的概率会收敛到一个数。最终的推荐列表中物品的权重就是物品节点的访问概率\(PR(v)\)。

\[PR(v) = \left\{ \begin{array}{ll} \sum_{v' \in \text{in}(v)}\frac{PR(v')}{|\text{out}(v')|} & \text{if } v \ne v_u \\ 1 - \alpha + \alpha \sum_{v' \in \text{in}(v)}\frac{PR(v')}{|\text{out}(v')|} & \text{if } v = v_u \end{array} \right. \]

缺点：时间复杂度较高，解决：1. 减少迭代次数 2. 稀疏矩阵快速求逆

posted @ 2024-05-05 23:19 peterzh6 阅读(40) 评论(0) 编辑收藏举报

刷新页面返回顶部