微积分公式与运算法则

 

 

 

 

====================================

求导和积分的区别

 

1、定义不同：

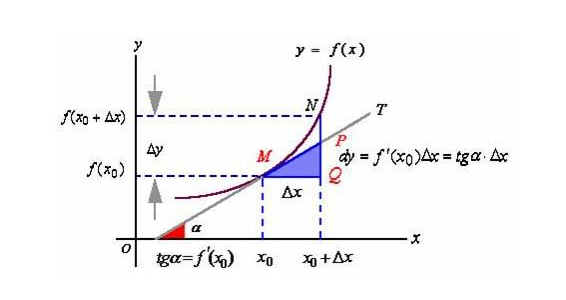
求导：当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。

在一个函数存在导数时，称这个函数可导或者可微分。

另外，可导的函数一定连续。不连续的函数一定不可导。

 

积分：通常分为定积分和不定积分两种。

直观地说，对于一个给定的正实值函数，在一个实数区间上的定积分可以理解为在坐标平面上，

由曲线、直线以及轴围成的曲边梯形的面积值（一种确定的实数值）。

 

 

2、表示方法不同

求导是数学中的名词，即对函数进行求导，用 f'(x)表示。

积分符号（Signs for Definite Integrals）是莱布尼茨于1675年以“omn.l”表示l的总和（积分（Integrals）），

而omn为omnia（意即所有、全部）之缩写。其后他又改写为 ∫，以“∫l”表示所有l的总和（Summa）。∫为字母s的拉长。

 

3、实际的物理意义不同

导数可以表示运动物体的瞬时速度和加速度、可以表示曲线在一点的斜率、还可以表示经济学中的边际和弹性。

实际操作中，很多时候需要知道精确的数值。要求简单几何形体的面积或体积，这就需要使用到积分的概念。

比如一个长方体状的游泳池的容积可以用长×宽×高求出。但如果游泳池是卵形、抛物型或更加不规则的形状，就需要用积分来求出容积。