红黑树，B- , B+树的理解

红黑树是一种近似平衡的二叉查找树，最长路径长度不超过最短路径长度的2倍：

HashMap为什么底层不选用AVL树:

AVL树是一棵严格的平衡树，它所有的子树都满足二叉平衡树的定义。因此AVL树高被严格控制在XXX，因此AVL树的查找比较高效。但AVL树插入、删除结点后旋转的次数比红黑树多。

红黑树用非严格的平衡来降低插入删除时旋转的次数,最长路径长度不超过最短路径长度的2倍。

因此，如果你的业务中查找远远多于插入、删除，那选AVL树； 
如果查找、插入、删除频率差不多，那么选择红黑树。

红黑树5个性质：

1.根节点为黑色节点

2.红色节点不能连续，也就是红色节点的孩子节点和父节点都不能是红色节，红色节点的孩子节点一定是黑色节点。

3.叶子节点一定是黑色（也就是空节点）

4.每一个节点到叶子节点的黑色节点的个数都是相同的

5.新插入的节点一定是红色

 

主要是插入过程：（最多需要两次旋转就可以达到红黑树平衡，主要是通过变色来代替了一部分旋转，但是变色的代价是很低的）

1.如果插入的节点父节点是黑色直接插入

2.插入节点的是红色，就改变父节点（红色变为黑色）和祖父节点（黑色变为红色）,可能有时候父节点的兄弟节点也要变色。

这个时候一般会出现冲突，那么我们先旋转，再看是否颜色仍然冲突，如果仍然冲突，我们就改变冲突节点的父节点和祖父节点。再进行同样的操作。

参考：

https://www.cnblogs.com/CarpenterLee/p/5503882.html

 

删除过程，假如要删除节点p：（最多只用旋转3次就能删除一个节点）

只有删除点是BLACK的时候，才会触发调整函数，因为删除RED节点不会破坏红黑树的任何约束

假如p的左右节点都为空，就直接删除这个节点p

假如p的左或者右节点不为空，那么我们就是要找到这个节点后继。

1.t的右子树不空，则t的后继是其右子树中最小的那个元素。

2.t的右孩子为空，则t的后继是其第一个向左走的祖先。

那么我们接下来删除p节点，用t代替p，再去用上面的操作重复删除t的这样一个操作（在这个过程中我们会有旋转也会有颜色的变化）。

参考：

https://www.cnblogs.com/CarpenterLee/p/5525688.html

 

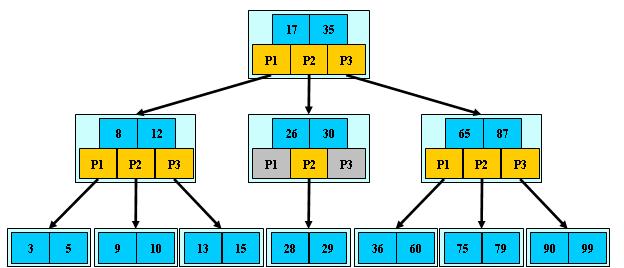
B-树的性质：

一棵m阶B-树

1.根结点至少有两个子女；

2.每个非根节点所包含的关键字个数最多m-1个

3.所有关键字分布在整颗树中

4. 任何一个关键字只能分布在一个节点中

5.搜索有可能在非叶子节点结束

 

 

 

 

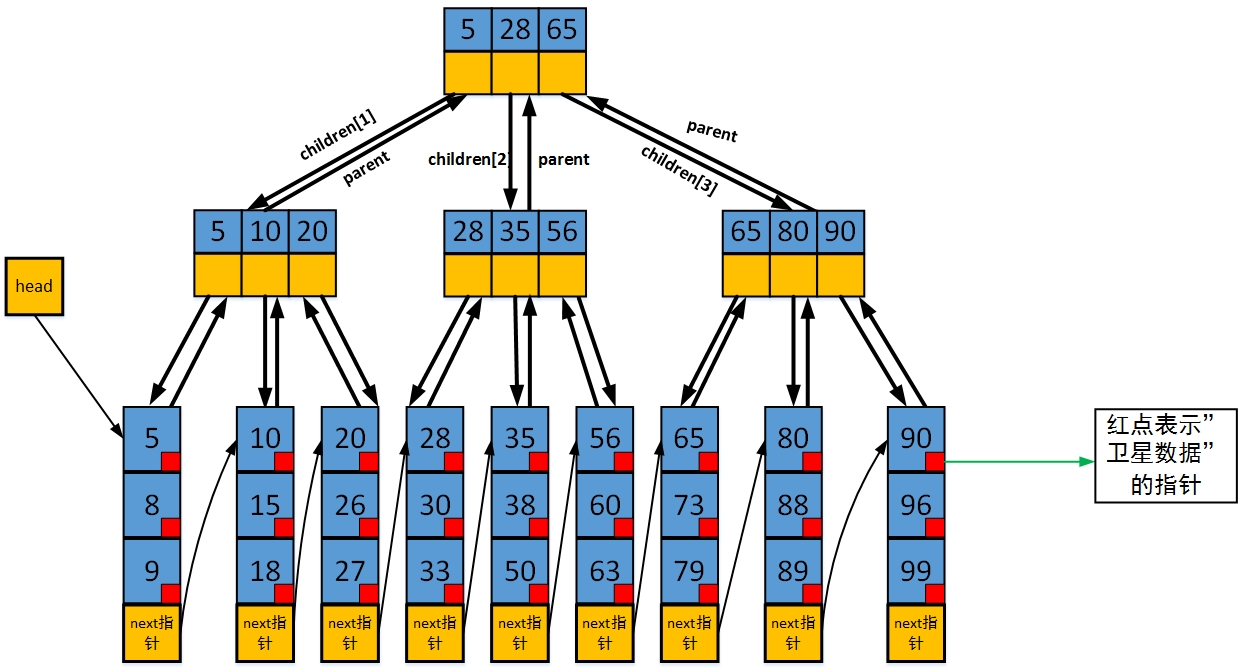
B+树的性质：

1.有n棵子树的结点中含有n个关键字；

2. 所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。

3. 所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字

 

对于B+树的搜索：

B+树的头指针有两个，一个指向根节点，另一个指向关键字最小的元素，因此B+树有两种遍历的方式：

1. 从根节点开始随机查询

2.从最小关键词顺序查询

 

 

对于一个m路B+树：

它的深度应该是logceil（m/2）n到logm n之间

在选择数据库索引的时候很大一个因素是减少读写磁盘

 

页表的目的是扩展内存+加速磁盘读写。一个页（Page）通常4K（等于磁盘数据块block的大小，见inode与block的分析），从磁盘读写的角度出发，操作系统每次以页为单位将内容从磁盘加载到内存（以摊分寻道成本），修改页后，再择期将该页写回磁盘。考虑到页表的良好性质，可以使每个节点的大小约等于一个页（使m非常大），这每次加载的一个页就能完整覆盖一个节点，以便选择下一层子树；对子树同理。对于页表来说，AVL（或RBT）相当于1个key+2个子树的B树，由于逻辑上相邻的节点，物理上通常不相邻，因此，读入一个4k页，页面内绝大部分空间都将是无效数据。

 

假设key、子树节点指针均占用4B，则B树节点最大m * (4 + 4) = 8m B；页面大小4KB。则m = 4 * 1024 / 8 = 512，一个512叉的B树，1000w的数据，深度最大 log(512/2)(10^7) = 3.02 ~= 4。对比二叉树如AVL的深度为log(2)(10^7) = 23.25 ~= 24，相差了5倍以上。震惊！B树索引深度竟然如此！

 

https://monkeysayhi.github.io/2018/03/06/%E6%B5%85%E8%B0%88MySQL%E7%9A%84B%E6%A0%91%E7%B4%A2%E5%BC%95%E4%B8%8E%E7%B4%A2%E5%BC%95%E4%BC%98%E5%8C%96/

为什么数据库不采用普通的AVL树？

普通的二分查找，二叉树可以把速度提升到O(log(n,2))，查询的瓶颈在于树的深度，最坏的情况要查找到二叉树的最深层，由于，每查找深一层，就要访问更深一层的索引文件。在多达数G的索引文件中，这将是很大的开销。所以，尽量把数据结构设计的更为‘矮胖’一点就可以减少访问的层数。所以就想到了B+，B-树。

为了减少磁盘IO，我们需要进行进行磁盘预读，普通的AVL树一个节点都只有一个关键字，不适合进行磁盘预读。

因此我们需要多路平衡树的存在，就可以充分利用磁盘预读，每个节点（一个页记录）都有多个关键字，那么我们磁盘IO的次数会减少。

为什么说B+树比B 树更适合实际应用中操作系统的文件索引和数据库索引？

1.B+树的磁盘读写代价更低 
B+树的内部节点并没有指向关键字具体信息的指针，因此其内部节点相对B树更小，如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多（也就是一个页记录，B+树页记录的关键字的个数比B-树一个节点存的关键字个数更多），一次性读入内存的需要查找的关键字也就越多，相对IO读写次数就降低了。

2.B+树的查询效率更加稳定 
由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

3.B+树还有一个最大的好处，方便扫库，B树必须用中序遍历的方法按序扫库，而B+树直接从叶子结点挨个扫一遍就完了（叶子节点层还维护了一个链表），B+树支持range-query非常方便，而B树不支持。这是数据库选用B+树的最主要原因

讲的很棒：https://blog.csdn.net/weixin_30531261/article/details/79312676

对了，在每个页节点，由于里面的数据是有序的，所以我们采用的是二分查找