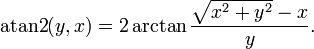Definition
In terms of the standard arctan function, whose range is (−π/2, π/2), it can be expressed as follows:
Notes:
- This produces results in the range (−π, π], which can be mapped to [0, 2π) by adding 2π to negative values.
- Traditionally, atan2(0, 0) is undefined.
- The C function atan2, and most other computer implementations, are designed to reduce the effort of transforming cartesian to polar coordinates and so always define atan2(0, 0). On implementations without signed zero, or when given positive zero arguments, it is normally defined as 0. It will always return a value in the range [−π, π] rather than raising an error or returning a NaN (Not a Number).
- Systems supporting symbolic mathematics normally return an undefined value for atan2(0,0) or otherwise signal that an abnormal condition has arisen.
- For systems implementing signed zero, infinities, or Not a Number (for example IEEE floating point), it is usual to implement reasonable extensions which may extend the range of values produced to include −π and −0. These also may return NaN or raise an exception when given a NaN argument.
The free math library FDLIBM (Freely Distributable LIBM) available from netlib has source code showing how it implements atan2 including handling the various IEEE exceptional values.
For systems without a hardware multiplier the function atan2 can be implemented in a numerically reliable manner by the CORDIC method. Thus implementations ofatan(y) will probably choose to compute atan2(y,1).
The following expression derived from the tangent half-angle formula can also be used to define atan2.
This expression may be more suited for symbolic use than the definition above. However it is unsuitable for floating point computational use as it is undefined fory = 0, x < 0 and may overflow near these regions. The formula gives an NaN or raises an error for atan2(0, 0), but this is not an issue since atan2(0, 0) is not defined.
A variant of the last formula is sometimes used in high precision computation. This avoids overflow but is always undefined when y = 0: