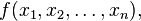博客园  :: 首页  :: 新随笔  :: 联系 :: 订阅 订阅  :: 管理

海森矩阵

Posted on 2012-04-07 23:04  月不识己  阅读(1139)  评论(0)  编辑  收藏  举报

在数学中，海森矩阵（Hessian matrix 或 Hessian）是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵，此函数如下：

f(x_1, x_2, \dots, x_n),

如果 f 所有的二阶导数都存在，那么 f 的海森矩阵即：

H(f)_{ij}(x) = D_i D_j f(x)

其中 x = (x_1, x_2, \dots, x_n)，即

H(f) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\,\partial x_n} \\ \\ \frac{\partial^2 f}{\partial x_2\,\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\,\partial x_n} \\ \\ \vdots & \vdots & \ddots & \vdots \\ \\ \frac{\partial^2 f}{\partial x_n\,\partial x_1} & \frac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}

（也有人把海森定义为以上矩阵的行列式） 海森矩阵被应用于牛顿法解决的大规模优化问题。

首先把变量名改成 x1 x2 ，并且确保之前 syms 过，即在之前写上：

syms x1 x2;

也就是 f 的表达式变成：

f = (x1 + x2) ^ 4 + x2 ^ 2

然后，梯度和海森矩阵分别为：

g = jacobian(f);
h = jacobian(g);

 

function H=hessian(f,x,x0)

% H=hessian(f,x) 计算表达式
% H=hessian(f,x,x0) 计算hessian矩阵的值 x0为x的初值

%$copyright by$ LUO sir

switch  nargin
    case 1
    error('please input variables in f(x)')

    case 2
        H=subhessian(f,x);
 
    case 3
        H=subhessian(f,x,x0);
        x=x0;
        H=subs(H);
    otherwise
       
         error('too many arguments or nothing')         
end

function HH=subhessian(f,x,x0)
 
n=length(x);

J=jacobian(f,x);
HH=[];
HH=sym(HH);
for i=1:n
HH(i,:)=jacobian(J(1,i),x);
end