计组-数据的表示和运算学习笔记
数制与编码
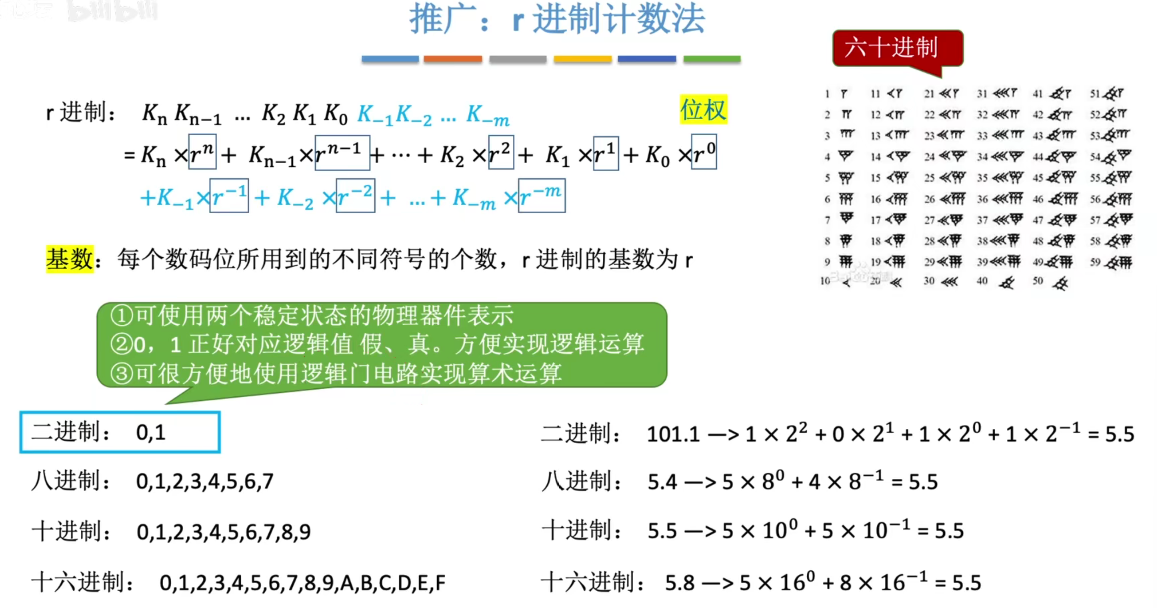
进制

十进制转换为任意进制数
常采用基数乘除法,这种转换方法对十进制数的整数部分和小数部分将分别进行处理
对整数部分采用除基取余法(先余为低位,后余为高位)
对小数部分采用乘基取整法(先整为高位,后整位低位)
定点数的编码表示
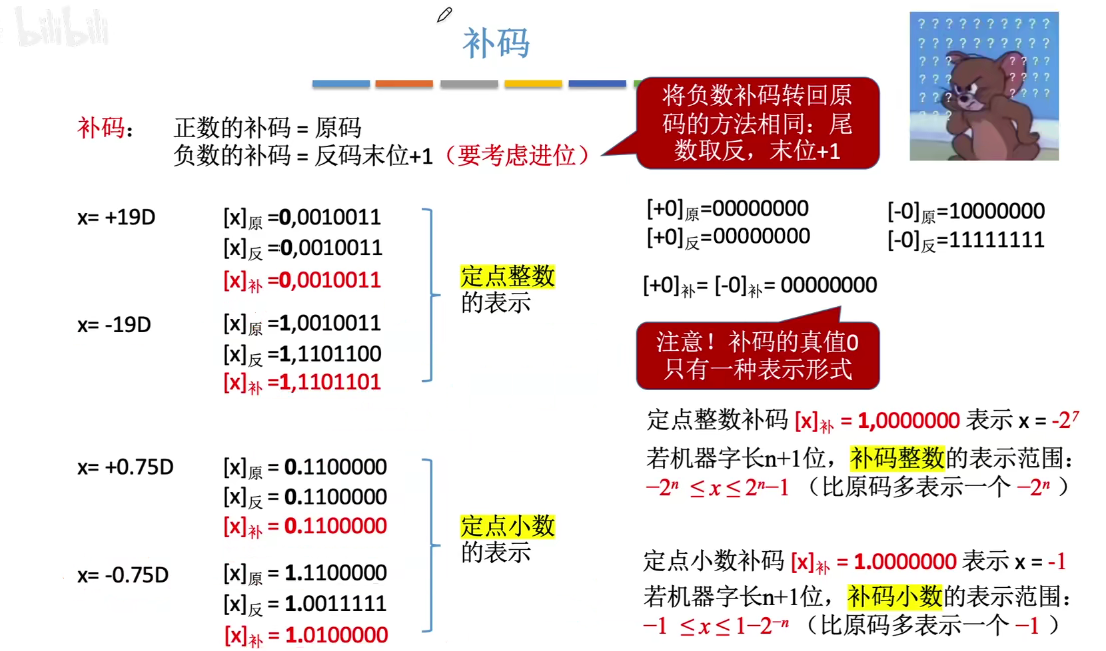
定点数表示小数和整数,主要有编码表示法:原码、补码、反码和移码
其中原码和反码表示整数时,都会产生正负零,在位数相等的情况下所表示数的范围比补码表示整数的范围少一个
正数形式下的 原码,反码,补码都是相同的,只是负数形式不一致
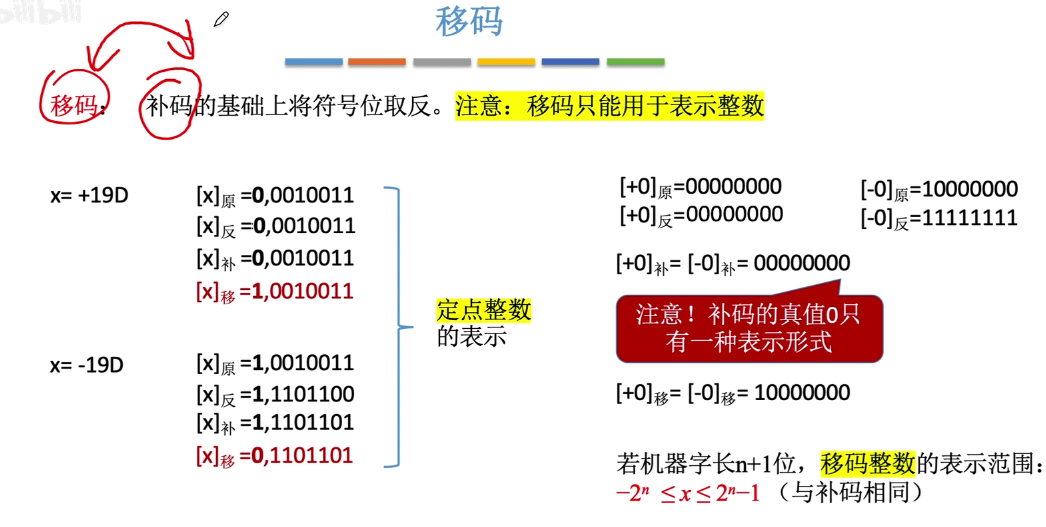
移码的一个重要性质:当真值不断增大时,移码也在不断增大
移码主要用于表示阶数
运算方法和运算电路
基本运算部件
在计算机中,运算器由算术逻辑单元(ALU)、移位器、状态寄存器和通用寄存器组等组成
ALU的核心部件是加法器
ALU是一种功能较强的组合逻辑电路,它能进行多种算术运算和逻辑运算。
由于加、减、乘、除运算最终都可以归结为加法运算,因此ALU的核心是带标志加法器
定点数的移位运算
1️⃣算术移位(针对带符号数)
-
原码的算术移位
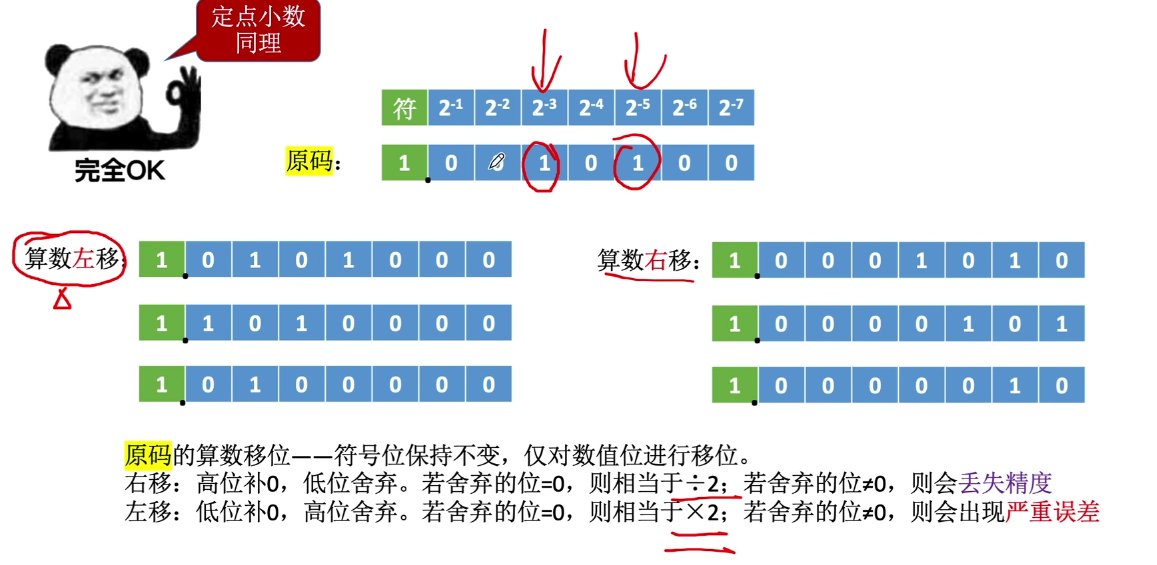
-
反码的算术移位
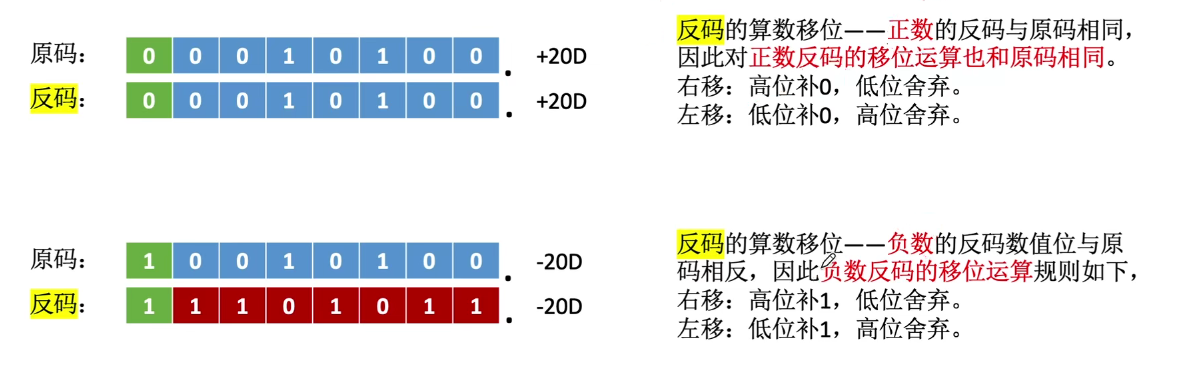
-
补码的算术移位
补码的最右边的第一个1的右边可看作是原码
补码最右边的第一个1的左边可看作是反码
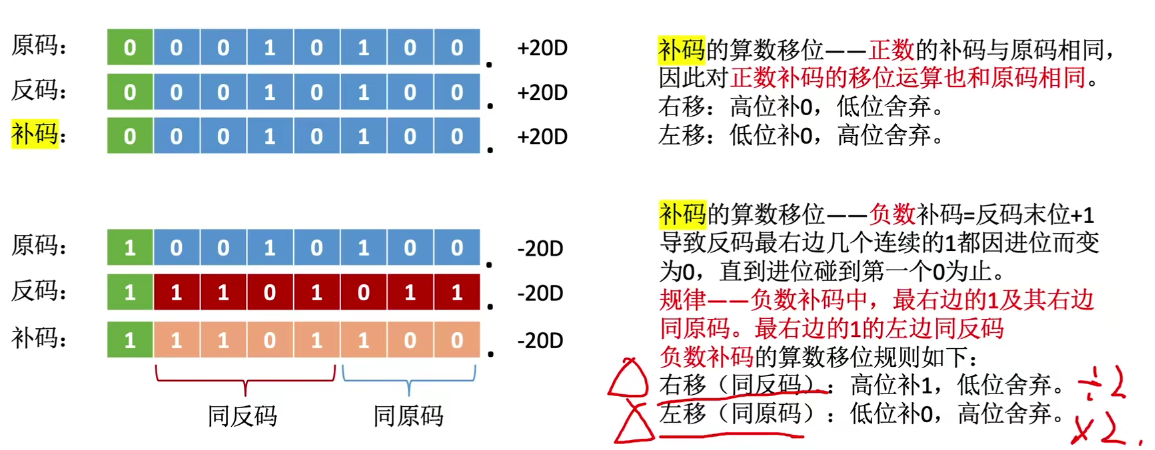
2️⃣逻辑移位(针对无符号数)

3️⃣循环移位
循环移位分为带进位标志位CF的循环移位(大循环)和不带进位标志位的循环移位(小循环)
定点数的加减运算
原码实现减法运算在电路上比较困难,主要是采用补码进行减法运算

补码的加减法运算
将减法运算也看成是 加法运算,
将A-B 转为 A+(-B)的补码进行加法运算
按二进制运算规则计算,逢二进一
符号位和数值位一起参与运算
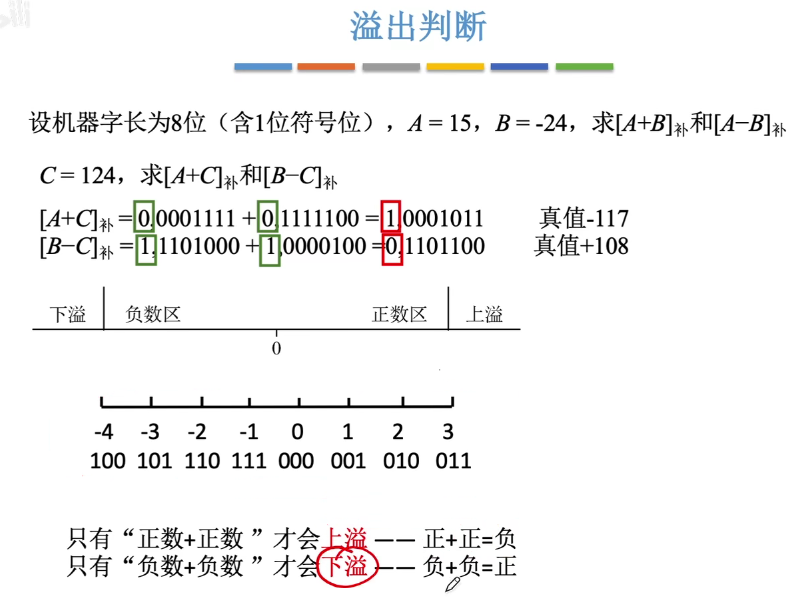
溢出判断
只有 两个正数相加 变成 负数 代表上溢 。 两个负数相加 变成正数 代表下溢
从符号的角度来看:就是两个相同的符号的数字进行加法操作,得出的结果是不同的符号,即代表溢出了(计算出错了)
有3种 判断补码加减运算是否溢出的方法
1️⃣采用一位符号位,根据逻辑运算式
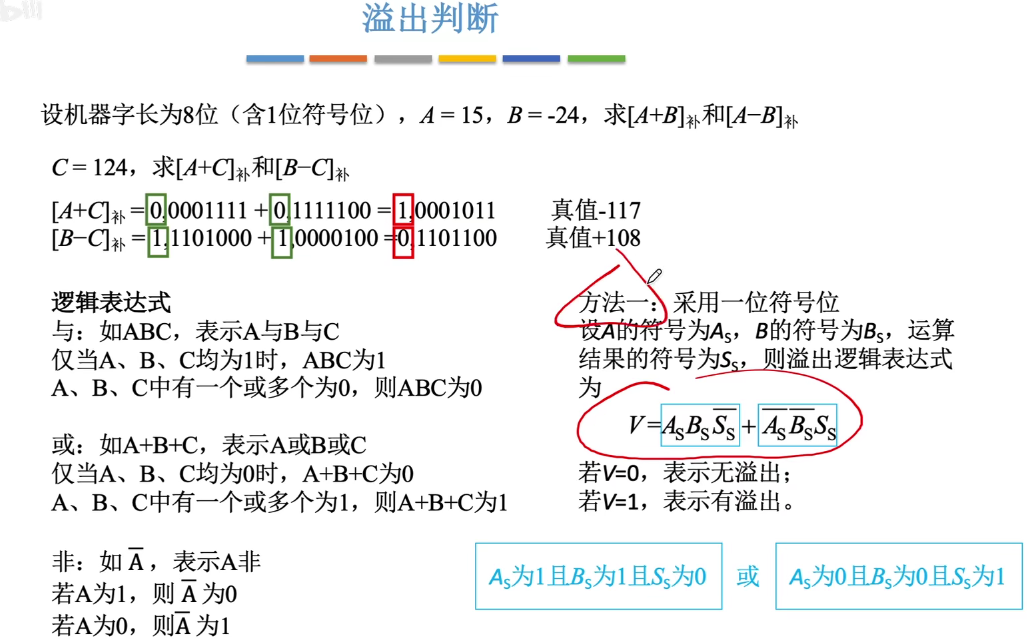
2️⃣

3️⃣采用双符号位
实际存储数据时,只会保存一位符号位,在进行运算时才会复制一个相同的符号位

符号扩展

定点数的乘除运算
乘法运算由累加和右移操作实现,可分为原码一位乘法 和 补码一位乘法
1️⃣原码一位乘法
特点:符号位和数值位分开求,乘积的符号位由两个数的符号位进行“异或”操作得到
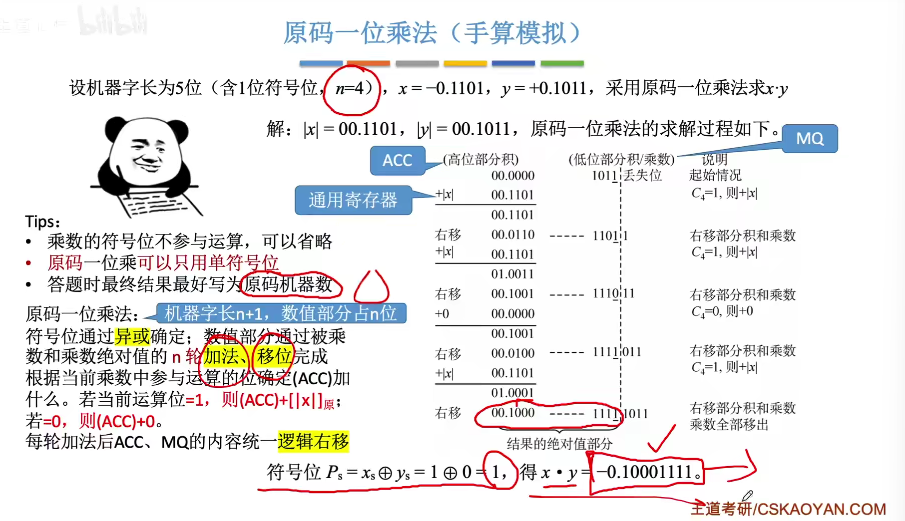
根据乘数当前位,是0还是1,若是1,就会加上被乘数然后进行一次逻辑右移
2️⃣补码一位乘法
是一种有符号数的乘法,采用相加和相减操作计算补码数据的乘积
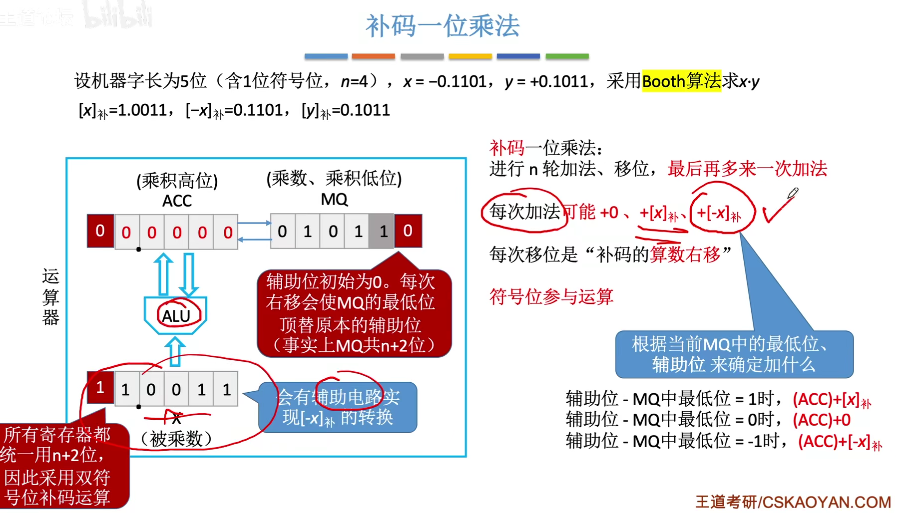
MQ(乘商寄存器)中保存乘数(用补码表示的单符号位,最后一位是辅助位)和乘积的低位部分
X(通用的操作数寄存器)中保存被乘数(用补码表示的双符号位)
ACC(累加器)保存乘积的高位部分(初始为全0,也是采用双符号位)
进行算术右移,若为正数,右移后补0,若为负数,右移后补1

最后多进行了一次加法(加完后不需移位),即若有n个数值位,就进行n+1次加法,n次算术右移
除法运算
原码除法运算,2种
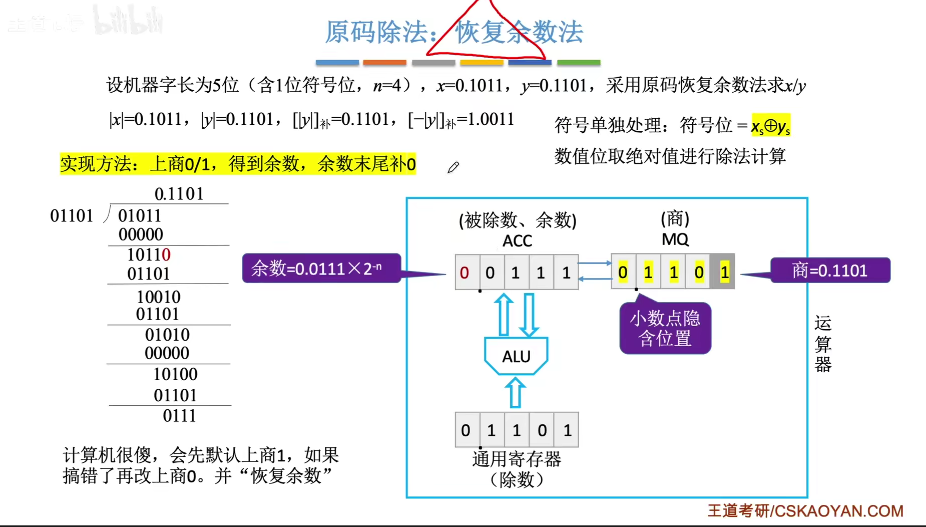
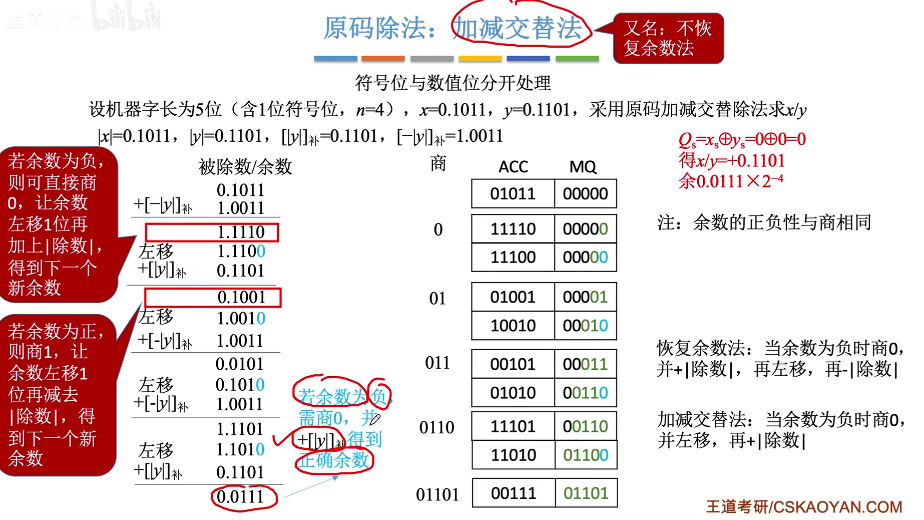
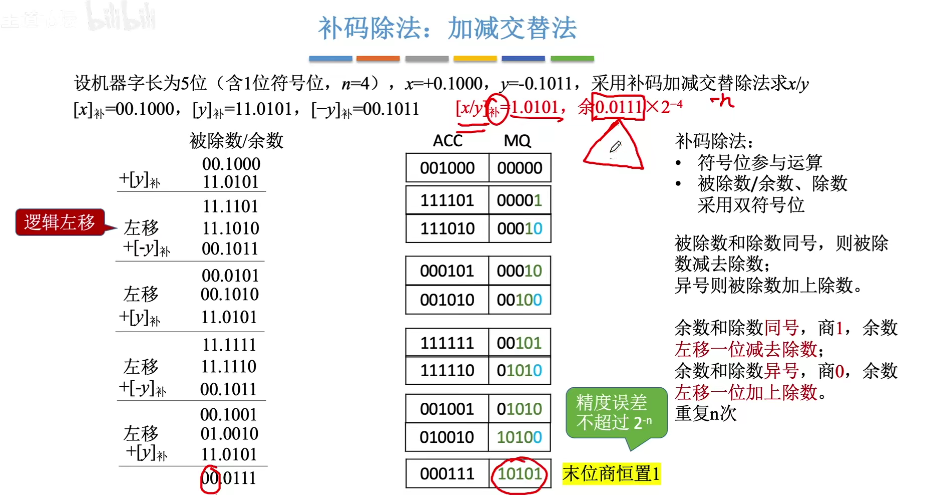
补码除法运算
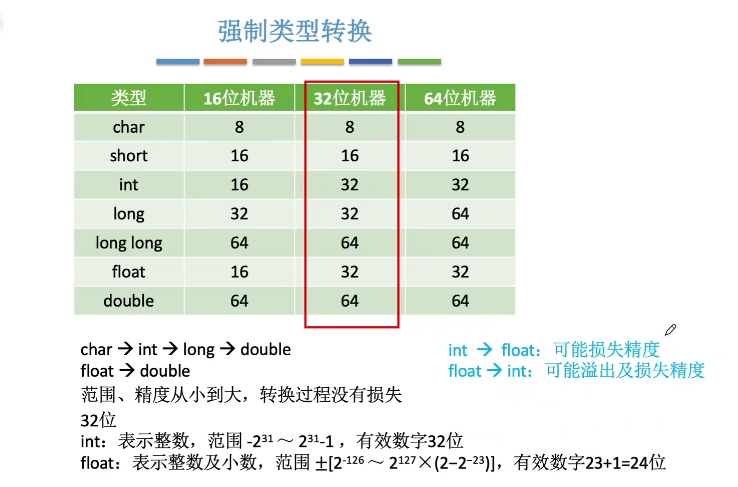
整数的类型转换
C语言中,有符号整数都是采用补码进行存储的

无符号数和符号数之间的转换,只是改变解释方式
其中长整型向短整型转换时,如int 改为 short存储时,是直接对二进制位进行截断,然后解释后面的位数(4字节转为2字节,重新解释后面16位二进制位为short类型存储的数)
短整型向长整型转换时,进行符号扩展(是有符号数),当为无符号数就直接补0即可
char类型为8位的无符号整数,在强制转为int类型时直接在高位补0即可
数据的存储和排列
在存储数据时,数据从低位到高位可以按从左到右排列,也可以按从右到左排列
一个整型int数据 为01234567H 其中01H为最高有效字节(MSB),67H为最低有效字节(LSB)
大端方式:从左到右,按最高有效字节到最低有效字节的方式存储,即MSB存储在低地址
小端方式:从左到右,按最低有效字节到最高有效字节的方式存储,即LSB存储在低地址
💽数据按边界方式存储
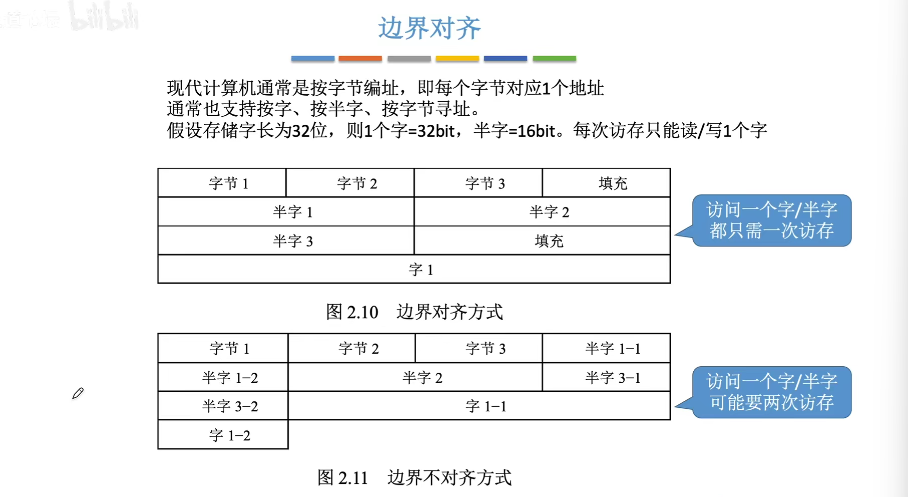
边界对齐方式相对于不对齐方式是一种以空间换时间的思想
RISC通常采用边界对齐方式,为了更加方便的实现流水线(取指令)
浮点数的表示和运算
浮点数表示法是指以适当的形式将比例因子表示在数据中,让小数点的位置根据需要而浮动。
这样在位数有限的情况下,既扩大了数的表示范围,又保持了数的有效精度
1️⃣第一种浮点数表示
32位 浮点数由 数符(1位),阶码(8位 移码表示)和 尾数(23位,一般用定点原码表示)组成
阶码的位数反映浮点数的表示范围,尾数的位数反映浮点数的精度
用原码表示尾数时,浮点数的表示范围也是关于原点对称的
- 运算结果大于最大正数时称为正上溢,小于绝对值最大负数时称为负上溢,正上溢和负上溢统称上溢。
- 数据一旦产生上溢,计算机必须中断运算操作,进行溢出处理。
- 当运算结果在0至最小正数之间时称为正下溢,在0至绝对值最小负数之间时称为负下溢,正下溢和负下溢统称下溢。
- 数据下溢时,浮点数值趋于零,计算机仅将其当作机器零处理。

浮点数的规格化
因为尾数的位数决定了浮点数的有效数位,有效数位越多,数据的精度就越高。
为了使有效数位(二进制中1为有效数位)尽量占满尾数数位,会对浮点数进行规格化,通过对尾数的移位和改变阶码,
使非零的浮点数在尾数的最高数位上保证是一个有效值(二进制中即是1)
2️⃣第二种浮点数的表示
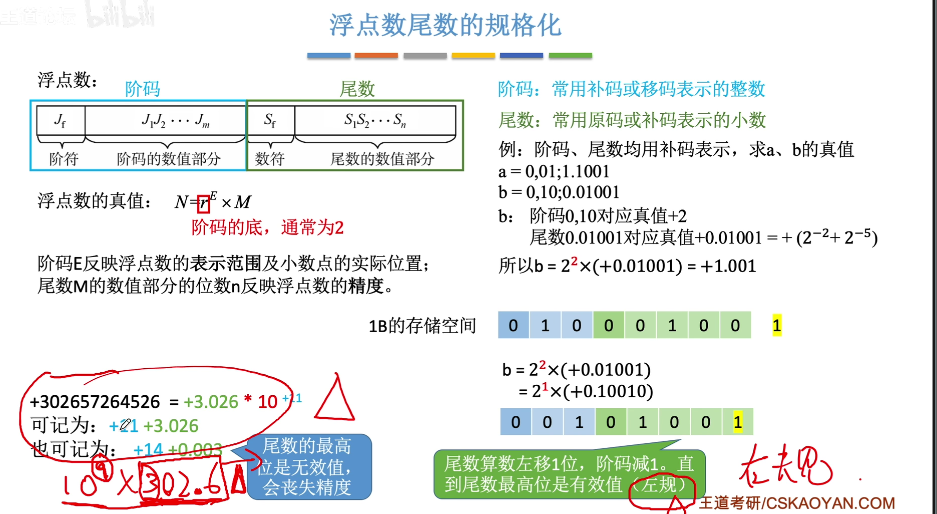
尾数的规格化

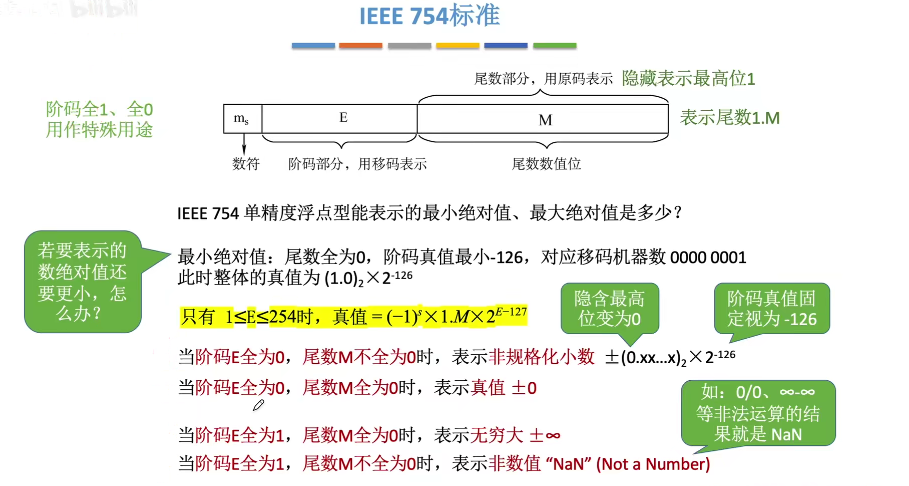
IEEE754标准
IEE754标准规定常用的浮点数格式有短浮点数(单精度,float型)、长浮点数(双精度、double型)和临时浮点数


在IEE754标准下,32位浮点数中的阶码的移码的偏置值为127( 2^(8-1)-1 )。
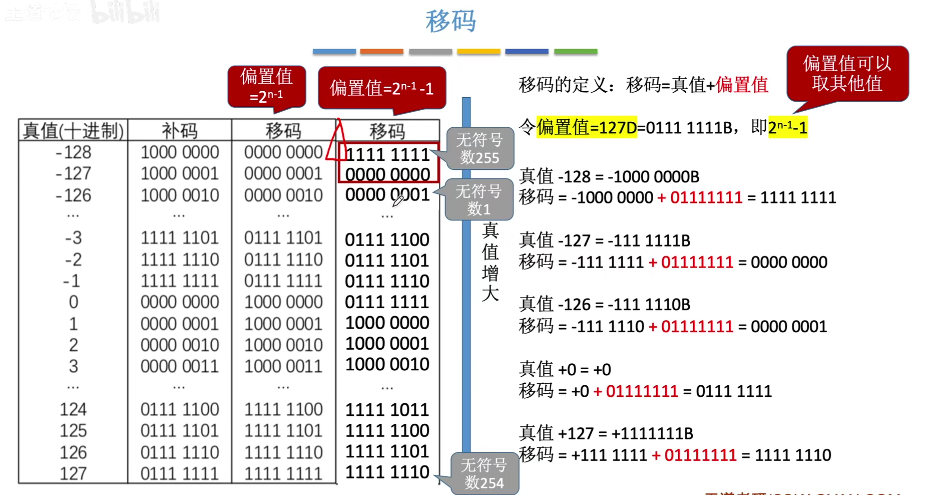
其中移码为真值+偏置值。如3+127=130。在32位浮点数中阶码为8位。
用无符号数解释时,阶码表示范围为0-255,其中0代表真值是-127,255代表-128都用作特殊情况,正常都是用移码1到254,即真值为-126到127的阶码。
阶码(全1,全0)的特殊用途
浮点数的加减运算
浮点数运算的特点是阶码运算和尾数运算分开进行
分为以下几步
1️⃣对阶
对阶的目的是使两个操作数的小数点位置对齐,即使得两个数的阶码相等
先求阶差,然后以小阶向大阶看齐,将阶码小的尾数右移一位(基数为2),阶码加一,直到两个数的阶码相等
在尾数右移时,舍弃掉有效位会产生误差,影响精度
2️⃣尾数求和
将对阶后的尾数按定点数加(减)运算规则运算,得到的尾数可能不是规格化的,所以下一步要进行规格化
3️⃣规格化
如IEE754标准要保证尾数为1.xxxx,然后存储时只需存储小数点后面的位数位(小数点之前的1是隐藏默认的)
4️⃣舍入
在对阶和尾数右规时,可能会对尾数进行右移,为保证运算精度,一般将低位移出的两位保留下来,参加中间过程的运算,最后将运算结果进行舍入,还原成IEE754的格式。
0舍1入法:类似于十进制的“四舍五入”法,运算结果保留位的最高数位为0,则舍去;最高数位为1,则在尾数的末尾加1,这样作可能导致尾数溢出,又要进行一次右规
恒置1法:只要因移位而丢失的位中有1,就把尾数末位置1,而不管原来是0还是1
截断法:直接截取所需位数,丢弃后面的所有位,这种方式最简单。
5️⃣溢出判断
在尾数规格化和尾数舍入时,可能会对阶码执行加/减运算。因此,必须考虑指数溢出的问题
若一个正指数即阶码的表示超出了范围(127或1023)则发生了指数上溢
若一个负指数超过了最小允许值,则发生指数下溢,通常把结果当成机器零来处理
对于IEEE754 标准下的32位浮点数,当阶码位全1(11111111)时,代表发生了指数上溢
当阶码为全0(00000000)时,代表指数下溢出,看成机器零进行处理

对于浮点数的溢出,并不是以尾数溢出来判断,尾数溢出可以通过右规得到纠正
浮点数的运算结果是否溢出主要看结果的指数是否发生了上溢,由指数上溢来判断
强制类型转换



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战