[Poj]1905——二分

[题目大意]

         给定一个弓形的弦长和弧长,求弓形弧中点到弦的距离.

[题解]

         对于仅知道弦长和弧长的弓形,我们是没有办法通过数学公式直接取得其半径的.(可能有...但是我不知道) 。这样的话,我们就考虑枚举一个量,使得整个弓形被确认下来.但是,对于实数类的变量，我们没有办法做到快速而又精确地枚举。这时我们就要考虑可不可以找到一个具有单调性的变量，对其进行“二分”——这一特殊的枚举。

         我们观察到,如果弓形的半角被确定了,那么整个弓形都会被确定.具体的关系非常的简单.

 

        

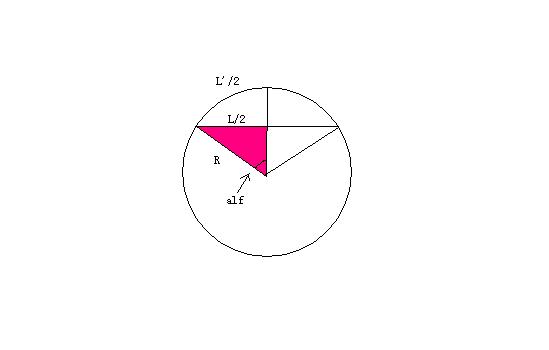
          alf即为弓形的半角.在弧度表示下，可得L'=L*alf/sin(alf).

          也就是说,L'只与alf这一个变量有关.现在就要在看函数h(x)=x/sin(x)在定义域(0,pai/2)之间的单调性了.

          可以对其求导或是直接用定义证明,不过最简单的就是在区间内随机几个点把函数值打印出来看一看.我在做的时候随便尝试了几个值,发现都是正的.这样可得h(x)是单调递增的,也就是说L'是随着alf的增加而增加的.

          这样我们就得到了一个具有单调性的变量alf,二分即可.

 

 

          同样的道理,本题也可以直接二分答案！

[代码]

//9938816       perseawe        1905    Accepted        876K    0MS     Pascal  521B    2012-03-17 21:10:01 

Const
  pi=3.1415926535897932384626433832795;
  eps=1e-12;

Var
  l,n,c,lp,ll,rr,mid:Extended;

function calc(alf:Extended):extended;
  begin
    exit(alf*l/sin(alf));
  end;

Begin
  readln(l,n,c);
  while not((l<0)and(n<0)and(c<0)) do
    begin
      lp:=l*(1+n*c);
      ll:=0;rr:=pi/2;
      repeat
        mid:=(ll+rr)/2;
        if calc(mid)<lp then ll:=mid else rr:=mid;
      until abs(ll-rr)<Eps;
      writeln((((l/2)/sin(mid))*(1-cos(mid))):0:3);
      readln(l,n,c);
    end;
End.

[启发]

         1.二分法的应用要注意在单调性的帮助之下，将枚举转化为二分。

         2.事后,我把h(x)=x/sin(x)在(0,pai)上的图像打印了出来.如图所示,证明我们的猜想是正确的.比赛时要大胆的猜,事后再小心的求证吧...

 

[用时]

         20min

[其他]