BNDS 2024/4/6模拟赛题解
T1 方程
描述
给出非负整数 \(N\) ，统计不定方程 \(X+Y^2+Z^3=N\) 的非负整数解 \((X,Y,Z)\) 的数量。
输入
输入数据，包含一个非负整数 \(N\)。
输出
输出数据，包含一个非负整数表示解的数量。
数据范围
40%的数据，\(N<=10000\)
60%的数据，\(N<=10^8\)
100%的数据，\(N<=10^{16}\)
分析
看到这个数据范围，应该只能从 \(Z\) 开始枚举。
移项后可得 \(X+Y^2=N-Z^3\) ，所以 \(0\leq Y\leq\sqrt{N-Z^3}\)。
注意，我们对于这个 \(Y\) 的具体值不感兴趣，我们只关心有多少个，而此时有 \((\sqrt{N-Z^3}+1)\) 个合法的 \(Y\)。此时， \(X=N-Z^3-Y^2\) ，显然也是一个非负整数。
所以，我们只需要从小到大枚举 \(Z\)，将 \((\sqrt{N-Z^3}+1)\) 添加到 \(ans\) 即可。
时间复杂度 \(O(\sqrt[3]{n})\)（sqrt视作常数复杂度）。
代码
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
ll n,ans;
int main(){
scanf("%lld",&n);
for(ll z=0;z*z*z<=n;z++)
ans+=ll(sqrt(n-z*z*z))+1ll;
printf("%lld",ans);
return 0;
}
T2 打砖块
描述
在一个凹槽中放置了 \(n\) 层砖块，最上面的一层有 \(n\) 块砖，从上到下每层依次减少一块砖。每块砖都有一个分值，敲掉这块砖就能得到相应的分值，如下图所示。
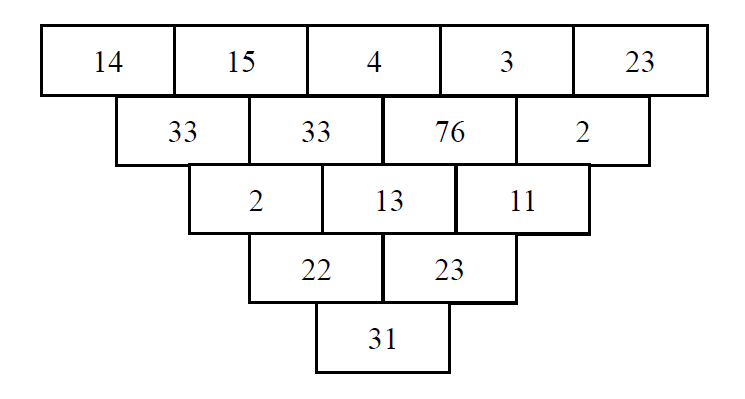
如果你要敲掉第 \(i\) 层的第 \(j\) 块砖的话，若 \(i=1\)，你可以直接敲掉它；若 \(i>1\)，则你必须先敲掉第 \((i-1)\) 层的第 \(j\) 和第 \(j+1\) 块砖。
你现在可以敲掉最多m块砖，求得分最多能有多少。
输入
输入的第一行为两个正整数 \(n,m\)；接下来 \(n\) 行，描述这 \(n\) 层砖块上的分值 \(a[i][j]\)，满足 \(0\leq a[i][j] \leq 100\)。
输出
输出仅一行为一个正整数，表示被敲掉砖块的最大价值总和。
数据范围
对于 \(20\%\) 的数据，满足\(1\leq n\leq 10, 1\leq m\leq 30\)；
对于 \(100\%\) 的数据，满足\(1\leq n\leq 50, 1\leq m\leq 500\)。
分析
一眼DP。
不过，看图之后发现，这个图并不存在决策单调性的性质。
不过旋转之后，就可以变成前 \(i\) 行与前 \(j\) 列的dp了。
这里通过一个输入就能完成旋转：
for(int j=1;j<=n;j++){
for(int i=n;i>=j;i--){
scanf("%d",&brick[i][j]);
}
}
设 \(dp[i][j][k]\) 代表前 \(i\) 行中，第 \(i\) 行选了 \(j\) 个、一共选了 \(k\) 个的最大值，然后进行dp即可。
还有就是记得提前算每行的前缀和\(sum[i][j]\)，优化速度。
PS：这道题的限制条件挺多的...所以写出了诸如 \(mxg, mxj, mxk\) 之类的抽象玩意。
\(g\) 是总共选择了多少，不能超过 \(\sum\limits_{a=1}^i a\) 的同时也不能超过 \(m\)。
\(j\) 不能超过 \(i\)（不能无中生有是吧），也不能超过 \(g\)。
\(k\) 同理，不能超过 \(i-1\) 的同时也不能超过 \(g-j\)。
最坏时间复杂度 \(O(nm^3)\)，实际上远远跑不到。
代码
#include<bits/stdc++.h>
#define N 55
using namespace std;
int n,m,brick[N][N],dp[N][N][2005],sum[N][N];
int ans;
int main(){
scanf("%d%d",&n,&m);
for(int j=1;j<=n;j++){
for(int i=n;i>=j;i--){
scanf("%d",&brick[i][j]);
}
}
/*
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cout<<brick[i][j]<<' ';
}
cout<<endl;
}*/
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
sum[i][j]=sum[i][j-1]+brick[i][j];
}
}
for(int i=1;i<=n;i++){
int mxg=min((i*(i+1))>>1,m),mxj,mxk;
for(int g=0;g<=mxg;g++){
mxj=min(i,g);
for(int j=0;j<=mxj;j++){
mxk=min(g-j,i-1);
for(int k=max(j-1,0);k<=mxk;k++){
if(dp[i-1][k][g-j]+sum[i][j]>dp[i][j][g])
dp[i][j][g]=dp[i-1][k][g-j]+sum[i][j];
}
}
}
}
for(int j=0;j<=n;j++){
if(dp[n][j][m]>ans)
ans=dp[n][j][m];
}
printf("%d",ans);
return 0;
}
T3 打砖块
描述
有两个长度为 \(N\) 的序列 \(A\) 和 \(B\)，在 \(A\) 和 \(B\) 中各任取一个数相加可以得到 \(N^2\) 个和，求这 \(N^2\) 个和中最小的 \(N\) 个。
输入
第一行输入一个正整数 \(N\) ；第二行 \(N\) 个整数 \(A_i\) 且 \(A_i\leq 10^9\)；第三行 \(N\) 个整数 \(B_i\) 且\(B_i\leq 10^9\)。
输出
输出仅一行，包含 \(N\) 个整数，从小到大输出这 \(N\) 个最小的和，相邻数字之间用空格隔开。
数据范围
对于 \(40\%\)的数据，满足\(1\leq N \leq 500\)；
对于 \(100\%\)的数据，满足\(1\leq N \leq 100000\)；
分析
如果这道题只要\(40\)分的话，其实二重循环枚举 \(A_i+B_i\) 即可。时间复杂度 \(O(n^2)\)。
如果你想要AC的话...
我们不妨建立一个优先队列，开始时将 \(A_i+B_1\) 放入优先队列里。如果此时的最小值为 \(A_x+B_1\)，则取出 \(A_x+B_1\)并记录，同时将 \(A_x+B_2\) 放入优先队列中。对于整个过程，也是同理：取出优先队列的最小值 \(A_x+B_y\)并记录，再将 \(A_x+B_{y+1}\) 放入优先队列中。重复 \(N\) 遍。时间复杂度 \(O(n\log n)\)。
代码
#include<bits/stdc++.h>
#define N 100005
using namespace std;
using PII=pair<int,int>;
bool cmp(PII a,PII b){
return a.first<b.first;
}
priority_queue<PII,vector<PII>,greater<PII> > q;
int n,a[N],b[N],cnt[N];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
cnt[i]=1;
scanf("%d",a+i);
}
for(int i=1;i<=n;i++){
scanf("%d",b+i);
}
sort(a+1,a+n+1);
sort(b+1,b+n+1);
for(int i=1;i<=n;i++){
q.push(make_pair(a[i]+b[1],i));
}
for(int i=1;i<=n;i++){
PII tmp=q.top();
q.pop();
printf("%d ",tmp.first);
q.push(make_pair(a[tmp.second]+b[++cnt[tmp.second]],tmp.second));
}
return 0;
}
T4 最小密度路径
描述
给出了一张有 \(N\) 个点 \(M\) 条边的加权有向无环图，接下来有 \(Q\) 个询问，每个询问包括 \(2\) 个节点 \(X\) 和 \(Y\)，要求算出从 \(X\) 到 \(Y\) 的一条路径，使得密度最小（密度的定义为，路径上边的权值和除以边的数量）。
输入
第 $1 行包括2个整数 \(N\) 和 \(M\)。
第 $2 $ 到 \(M+1\) 行，每行三个数字 \(A,B,W\) ，表示从 \(A\) 到 \(B\) 有一条权值为 \(W\) 的有向边。
第 \(M+2\) 行只有一个整数 \(Q\)。
接下来 \(Q\) 行，每行有两个正整数 \(X, Y\)，表示一个询问。
输出
对于每个询问输出一行，表示该询问的最小密度路径的密度（保留 \(3\) 位小数）。
如果不存在从 \(X\) 到 \(Y\) 的一条路径，则输出"OMG!"（不含引号）。
数据范围
对于 \(50\%\) 的数据，有 \(1\leq N\leq 10, 1\leq M\leq 100, 1\leq W\leq 1000, 1\leq Q\leq 1000\)；
对于 \(100\%\) 的数据，有 \(1\leq N\leq 50, 1\leq M\leq 1000, 1\leq W\leq 100000, 1\leq Q\leq 100000\)。
分析
考场上时间不够了。（主要是T2时间想的太久了）
所以写了个dfs爆搜。（喜得54分）
后来想了下，看到了数据范围，用Floyd应该没问题？再单独加一个记录多少步的数组，然后枚举一遍应该就行了。
（暴力DFS）代码
#include<bits/stdc++.h>
#define N 100005
#define M 55
using namespace std;
int n,m,Q;
const double INF=1145141919810.0;
struct EDGE{
int to,nxt,v;
}e[N];
int head[N],cnt=0;
double dis[M][M];
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].v=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs(int x,double sum,int edgeCnt,int origin)
{
if(x!=origin)
dis[origin][x]=min(dis[origin][x],sum/double(edgeCnt));
for(int i=head[x];i;i=e[i].nxt){
dfs(e[i].to,sum+double(e[i].v),edgeCnt+1,origin);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dis[i][j]=INF;
}
dis[i][i]=0;
}
for(int i=1;i<=n;i++)
dfs(i,0,0,i);
scanf("%d",&Q);
while(Q--){
int x,y;
scanf("%d%d",&x,&y);
if(dis[x][y]==INF)
printf("OMG!\n");
else
printf("%.3lf\n",dis[x][y]);
}
return 0;
}
AC代码
#define N 55
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
using namespace std;
const int INF = 0x3f3f3f3f;
int n, m, q;
double map[N][N][N];
double d[N][N];
inline void add(int from, int to, double dist) {
map[from][to][1] = min(map[from][to][1], dist);
}
inline void den() {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
if (map[i][j][k] != INF)
d[i][j] = min(d[i][j], map[i][j][k] / k);
}
void floyd() {
for (int t = 2; t <= n; t++)
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
map[i][j][t] = min(map[i][j][t], map[i][k][t - 1] + map[k][j][1]);
den();
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++)
map[i][j][k] = INF;
d[i][j] = INF;
}
for (int i = 1; i <= m; i++) {
int x, y, v;
scanf("%d%d%d", &x, &y, &v);
add(x, y, v);
}
floyd();
scanf("%d", &q);
for (int i = 1; i <= q; i++) {
int x, y;
scanf("%d%d", &x, &y);
if (d[x][y] == INF)
printf("OMG!\n");
else
printf("%0.3lf\n", d[x][y]);
}
}
