数据结构基础03-红黑树
红黑树
红黑树是一种自平衡的二叉树;
红黑树必须要遵循的规则:
-
1.节点是红色或黑色;
-
2.根节点为黑色;
-
3.每个叶子节点都是黑色的空节点;
-
4.红色节点不能有红色的父节点或子节点
-
5.从任一节点到叶子节点的黑色节点数必须一致;
红黑树的两大操作:变色和旋转
-
变色:将节点的颜色由黑变红,或者由红变黑
-
旋转:通过有两种旋转方式
-
左旋转:将右孩子替换父节点成为新的父节点,原父节点顺势左转成为新的父节点的左孩子;
-
右旋转:将左孩子替换父节点变成新的父节点,原父节点顺势向右成为新的父节点的右孩子;
-
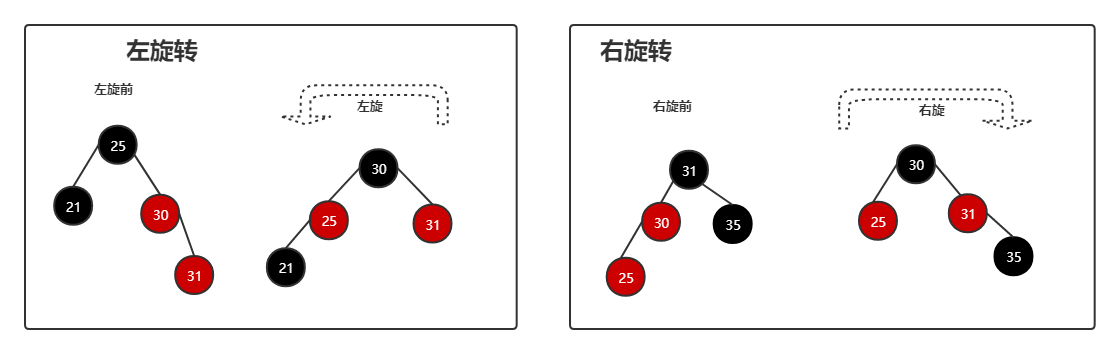
备注:新插入的节点默认是红色的;
红黑树插入新节点操作
情况1:新插入节点的父节点和父节点同一水平的叔叔节点,都是红色时
-
将父节点和叔叔节点变成黑色;
-
祖父节点变成红色;
-
如果祖父节点是根节点时,变成黑色;
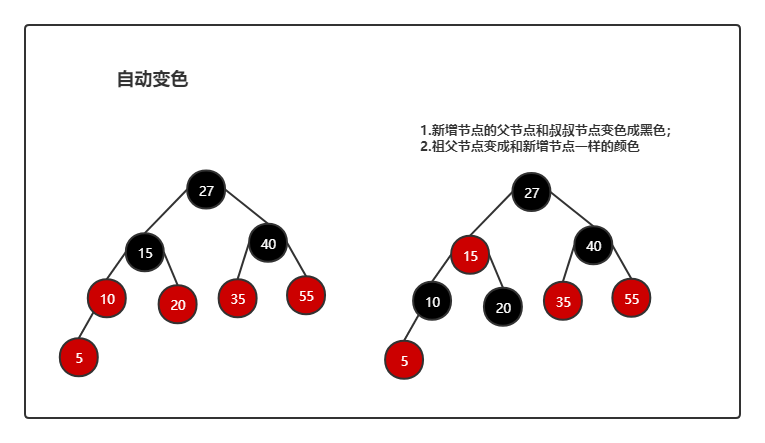
情况2:新插入节点的父节点为红色,父节点同一水平的叔叔节点为黑色
这种要根据新插入的节点,在根节点的插入位置不同,有不同的情况
-
最小子树的左节点增加左子节点
- 进行右旋操作
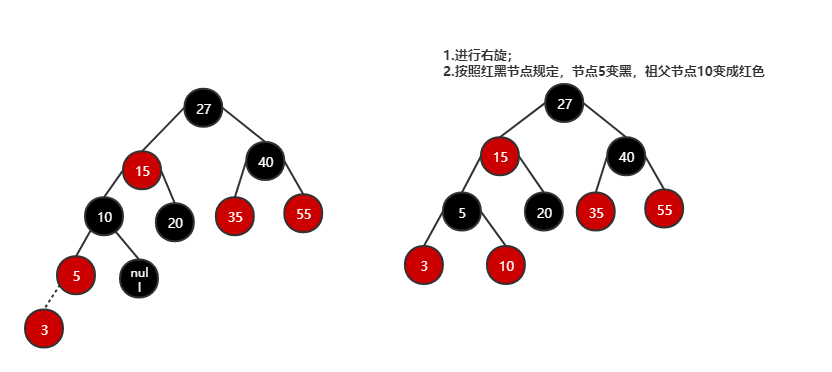
-
最小子树的左节点增加右子节点
-
先进行左旋,调整节点
-
再进行右旋,调整节点颜色
-
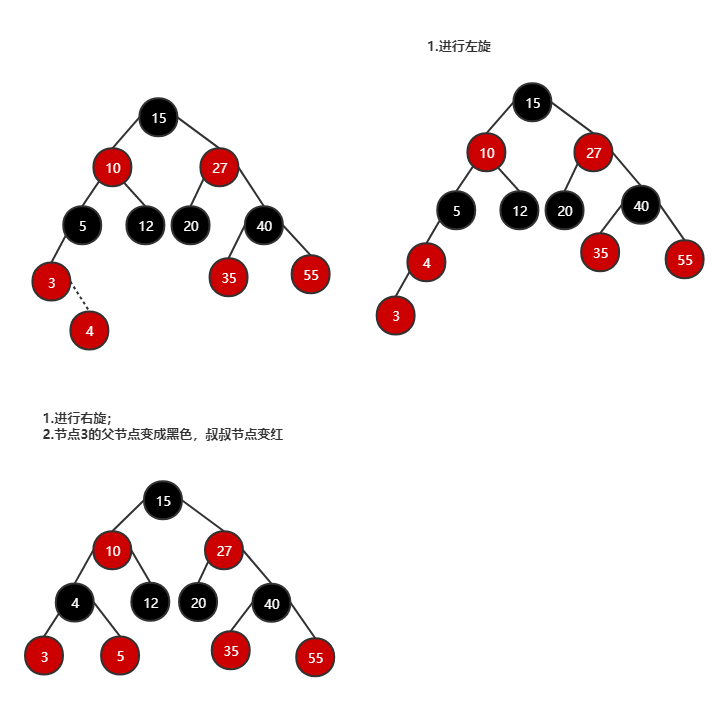
-
最小子树的右节点增加左子节点
-
进行右旋操作
-
再进行左旋操作
-

-
最小子树的右节点增加右子节点
- 进行左旋操作
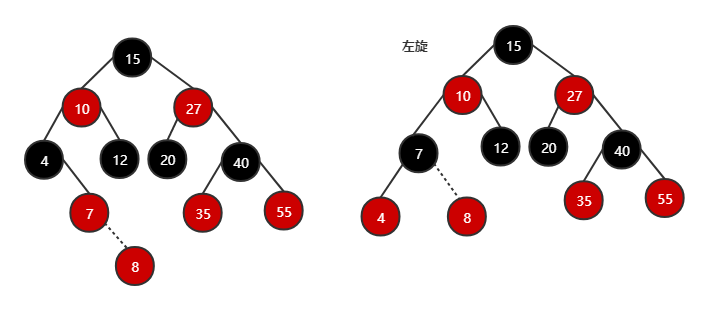
案例
- 逐个增加10 70 32 34 13 56 56 21 3 62 4
具体可以看我的另一篇博客:
https://www.cnblogs.com/perferect/p/13577085.html
实现代码(Java版本)
java中Map集合,在JDK1.8之后,Entry数组,同一个HASH的值存储改成了红黑树存储。以ConcurrentHashMap代码进行红黑树相关带啊分析;
以下代码的git地址:https://gitee.com/wuzhiaite/cs_java/blob/master/src/test/java/com/wuzhiaite/javaweb/base/bitree/RedBlackTree.java
-
TreeNode 代码
- 节点三个连接,一个颜色标记
class RedBlackNode< V extends Comparable<V>> {
RedBlackNode<V> parent; // 红黑树的连接
RedBlackNode<V> left;
RedBlackNode<V> right;
boolean red;
volatile V val;
RedBlackNode(V val,
RedBlackNode<V> parent) {
this.val = val ;
this.parent = parent ;
}
}
-
红黑树的结构
- 需要存放根节点
public final class RedBlackTree<V extends Comparable<V>> {
RedBlackNode root;
}
- 红黑树的插入操作
/**
* 1.查找插入值的父节点
* 2.进行值插入和红黑树自平衡
* @param v
* @return
*/
public RedBlackNode putTreeVal(V v){
boolean searched = false;
for (RedBlackNode<V> p = root;;) {
int dir = 0;V pv;
if (p == null) {//根节点
root = new RedBlackNode(v,null);
break;
}
else if ((pv = p.val).compareTo(v) < 0) //根节点值小于新插入值
dir = -1;
else if (pv.compareTo(v) > 0 )//跟节点值大于新插入节点
dir = 1;
else if (pv == v || (pv != null && pv.equals(pv)))//判断是否已经插入过
return p;
else{
//查找是否已经存在该节点,如果存在则返回该节点
//根的左子树进行查询判断
//根的右子树进行查询判断
if (!searched) {
RedBlackNode<V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.findTreeNode(v)) != null) ||
((ch = p.right) != null &&
(q = ch.findTreeNode(v)) != null))
return q;
}
}
//1.提前将p的值赋值给一个新的变量px
//2.根据上面值判断结果,如果新插入值小于节点p,则p赋值为左子树,否则赋值为右子树
//3.如果p为null,表示是可以插入值的节点
RedBlackNode<V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
RedBlackNode<V> x;
x = new RedBlackNode<V>(v,xp);//生成新的节点,父节点赋值为上面查询出来的可连接点
// if (x != null)
// f.prev = x;
//根据dir值,关联新生节点和父节点
if (dir <= 0)
xp.left = x;
else
xp.right = x;
if (!xp.red)//如果父节点是黑色的,则表明
x.red = true;
else {
root = balanceInsertion(root, x);//进行平衡插入数据
}
break;
}
}
return null;
}
/**
* 插入数据
* @param root
* @param x
* @return
*/
private RedBlackNode<V> balanceInsertion(RedBlackNode<V> root, RedBlackNode<V> x) {
x.red = true;
for (RedBlackNode<V> xp, xpp, xppl, xppr;;) {
//如果插入节点的父节点为空,则表示当前节点为根节点,变色并返回当前节点
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
//如果插入值的祖父节点空,或父节点是黑色时,返回父节点
else if (!xp.red || (xpp = xp.parent) == null)
return root;
/**
* xpp
* / \
* xp xppr
* /
* x
*下面的情况时父节点为红色,且祖父节点不为空时
*父节点是祖父节点的左节点时
*/
if (xp == (xppl = xpp.left)) {
//判断叔叔节点如果是红色,则父节点和叔叔节点变色
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;//祖父节点变红
x = xpp;//将祖父节点赋值给当前节点,用于判断祖父节点和祖父节点的父节点是否都为红色
}
//父节点和叔叔节点颜色不同时
else {
/**
* xpp
* / \
* xp xppr
* \
* x
*
* 如果要插入的节点是父节点的右节点时进行左转
* 即,新的节点给最小子树的左节点,新增右子节点时进行左转
*/
if (x == xp.right) {
root = rotateLeft(root, x = xp);//这里x=xp是因为,左旋是x替换xp的过程,所以用x=xp
xpp = (xp = x.parent) == null ? null : xp.parent;
}
/**
* xpp
* / \
* xp xppr
* /
* x
* 先变色再旋转
**/
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
/**
* 插入节点的父节点为祖父节点的右节点时
*/
else {
/**
* 父节点和兄弟节点为红色时,同时变得,并将x变更为祖父节点
* 判断祖父节点是否符合红黑树规则
*/
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
/**
* 异色进行旋转
*/
else {
/**
* xpp
* / \
* xpl xp
* /
* x
* 进行右旋
* xpp
* / \
* xpl xp
* \
* x
*/
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
/**
* 1.xp非空的时候,先进行变色,再进行左旋
* xp
* / \
* xpp x
* /
* xpl
*/
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
- 红黑树插入操作中设计到左旋和右旋操作
左旋操作
/**
*
* 进行左旋转
* @param root
* @param p
* @return
*/
private RedBlackNode<V> rotateLeft(RedBlackNode<V> root, RedBlackNode<V> p) {
RedBlackNode<V> r, pp, rl;
/**
* pp
* / \
* p ppr
* \
* r
* / \
* rl rr
* 左旋操作:
* 1.r节点的左节点rl变成p节点的左节点
* 2.r节点的父节点变成p的父节点
* 3.p的父节点变成r
* pp
* / \
* r ppr
* / \
* p rr
* /
* rl
*
*/
if (p != null && (r = p.right) != null) {
if ((rl = p.right = r.left) != null)
rl.parent = p;
if ((pp = r.parent = p.parent) == null)//如果pp节点为空,也即r为根节点,颜色变黑
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
右旋操作
/**
* 进行右旋
* @param root
* @param p
* @return
*/
private RedBlackNode<V> rotateRight(RedBlackNode<V> root, RedBlackNode<V> p) {
/**
* p
* / \
* l pr
* / \
* ll lr
* 右旋操作:
* 1.p节点的左节点变成l的右节点
* 2.l的父节点变成p的父节点
* 3.p的父节点变成l
* l
* / \
* ll p
* / \
* lr pr
*/
RedBlackNode<V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
其他操作-查找节点
- 查找红黑树中的节点,和所有二叉树一样进行二分法进行查询。代码也比较简单
//用于查找节点的父节点
final RedBlackNode<V> findTreeNode(V v) {
if (v != null) {
RedBlackNode<V> p = this;
do {
int dir; V pv; RedBlackNode<V> q;
RedBlackNode<V> pl = p.left, pr = p.right;
if ((pv = p.val).compareTo(v) > 0)//从左子树查询
p = pl;
else if ((pv = p.val).compareTo(v) < 0)//从右子树查询
p = pr;
else if ((pv = p.val) == v || (pv != null && p.val.equals(pv)))//如果刚好和当前节点相同,则返回
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
else if ((q = pr.findTreeNode(v)) != null)//如果没有,则循环遍历,知道查询的父节点P为null
return q;
else
p = pl;
} while (p != null);
}
return null;
}
其他操作-删除节点(比较复杂,了解)
-
红黑树节点删除涉及的情况比较多也比较复杂,大致分这几种:
-
删除节点是根节点的;
-
删除节点有左右节点的情况;
-
删除节点只有左节点情况
-
删除节点只有右节点情况。
-
-
删除的思路:
-
找到删除节点的临界节点,以上四种情况分别有不同处理,找到合适的临界节点做替换节点
-
调整树结构,将删除节点移位。
-
断开删除节点与左右父节点的关联,替换节点关联删除父节点
-
替换节点变色和进行左右旋操作,红黑树进行自平衡
-
-
具体代码如下:
/**
* 删除节点
* @param p
* @return
*/
public boolean removeTreeNode(RedBlackNode<V> p){
RedBlackNode<V> r, rl;
if ((r = root) == null || r.right == null ||
(rl = r.left) == null || rl.left == null)
return true;
try {
/**
* sp
* \
* p
* / \
* pl pr
* /
* s
* \
* sr
*/
RedBlackNode<V> replacement;
RedBlackNode<V> pl = p.left;
RedBlackNode<V> pr = p.right;
if (pl != null && pr != null) {
RedBlackNode<V> s = pr, sl;
/**
* 1.删除节点p的右节点pr
* 2.pr的左节点循环找到最小左子树的左节点s
*/
while ((sl = s.left) != null)
s = sl;
boolean c = s.red; s.red = p.red; p.red = c; //颜色交换
RedBlackNode<V> sr = s.right;
RedBlackNode<V> pp = p.parent;
/**
* pr
* \
* p
* 当pr==s时
* 要删除的节点只有一个右节点时,进行交换
*/
if (s == pr) {
p.parent = s;
s.right = p;
}
else {
/**
* 以下的数据处理逻辑是这样子的
* pp pp pp
* \ / /
* p s s
* / \ / \ / \
* pl pr ————> pl pr ————> pl pr
* / / /
* s p sr
* \ \
* sr sr
*
* 1.找到要删除节点p的右节点pr;
* 2.循环遍历pr的所有子节点的左节点,找到最小子树的左节点s;
* 3.p节点指向s的父节点,p成为s父节点的左子树;
* 4.p的右子树成为s节点的有子节点;
* 5.s的右子节点sr成为p的右子节点
* 6.s的成为p的左节点
*/
RedBlackNode<V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
if ((s.parent = pp) == null)
r = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
if (sr != null)
replacement = sr;
else
replacement = p;
}
/**
* 这个replacement分四种情况:
* 1.p有左右节点,且p为根节点的最小值子树的左节点(s),有sr右节点。则为右节点
* 2.上面没有右节点,则为p;
* 3.p只有左节点pl,replacement=pl
* 4.p只有右节点pr,replacement=pr
*/
else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
/**
* 用replacement元素替换要删除的p节点
*/
if (replacement != p) {
RedBlackNode<V> pp = replacement.parent = p.parent;//pr
if (pp == null)
r = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
/**
* 判断删除后的节点是否需要进行自平衡
*/
root = (p.red) ? r : balanceDeletion(r, replacement);
/**
* 删除p父亲节点和p节点的关联关系
*/
if (p == replacement) {
RedBlackNode<V> pp;
if ((pp = p.parent) != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
p.parent = null;
}
}
} finally {
}
return false;
}
/**
* 节点删除
* @param r
* @param x
* @return
*/
private RedBlackNode balanceDeletion(RedBlackNode<V> r, RedBlackNode<V> x) {
for (RedBlackNode<V> xp, xpl, xpr;;) {
/**
* 判断是否为根节点
*/
if (x == null || x == root)
return root;
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (x.red) {
x.red = false;
return root;
}
/**
* xp xp
* / \ /
* xpl(x) xpr x
* / \
* sl sr
*
*
* 已知:1.x为xp左节点且为黑色
* 2.xp节点肯定和x同色(因为红黑树不能有连续红色节点,删除掉中间节点后,只能都是红色或黑色,上面判断了x不能是红色)
* 操作:1.x的兄弟节点异色,进行左旋
*
* 上面分析了x(replacement)节点有5种情况
*/
else if ((xpl = xp.left) == x) {
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
xpr = (xp = x.parent) == null ? null : xp.right;
}
if (xpr == null)
x = xp;
else {
RedBlackNode<V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
xpr.red = true;
x = xp;
}
else {
if (sr == null || !sr.red) {
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ?
null : xp.right;
}
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
x = root;
}
}
}
else { // symmetric
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
RedBlackNode<V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号