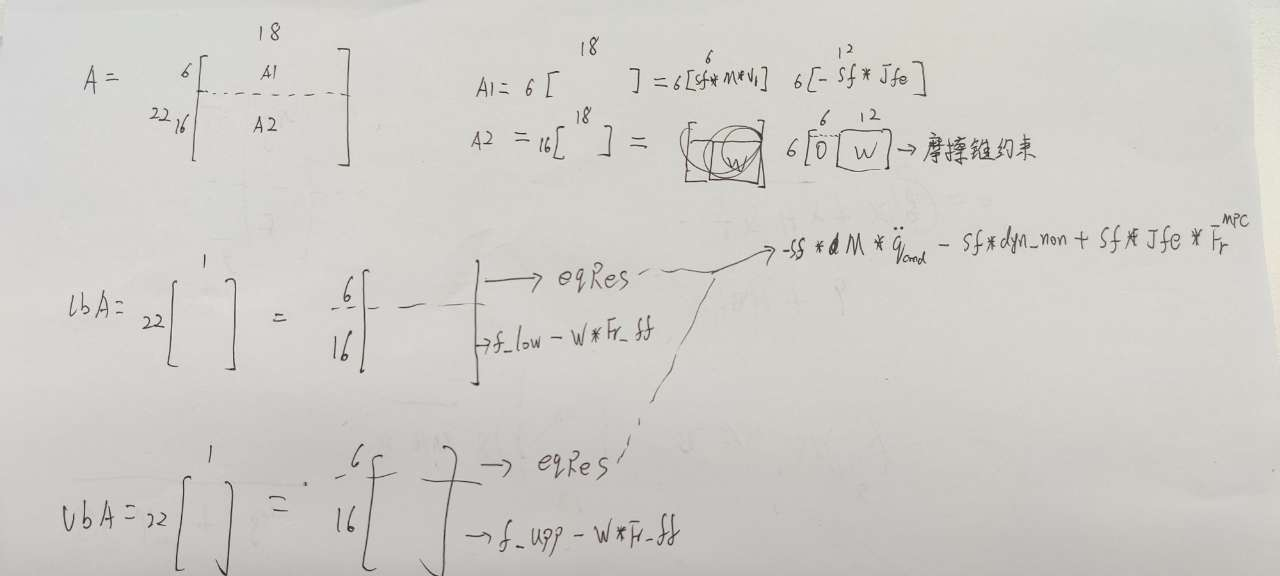青龙源码解析wbc

1. 任务管理：

WBC_walk task:
"static_Contact"; "Roll_Pitch_Yaw_Pz"; "RedundantJoints"; "PxPy"; "SwingLeg"; "HandTrack"; "HandTrackJoints"; "PosRot"

使能：
"static_Contact"； "RedundantJoints"； "SwingLeg"； "HandTrackJoints"； "PosRot"

WBC_stand task:
"static_Contact"； "HandTrackJoints"； "CoMTrack"； "HandTrackJoints"； "HipRPY"； "HeadRP"； "Pz"； "CoMXY_HipRPY"； "Roll_Pitch_Yaw"； "fixedWaist"

使能：
"static_Contact"； "HandTrackJoints"； "CoMXY_HipRPY"； "Pz"； "HeadRP"

2. 任务跟踪：

computeDdq()；

walk:

• static_Contact：
  errX,derrX,ddxDes,dxDes,kp,kd = 0；
  J,dJ读取雅可比，W = 1

• RedundantJoints：
  errX = Eigen::VectorXd::Zero(5);
  //21-22：头部关节
  //23-25：腰部关节
  errX(0) = 0 - q(21);
  errX(1) = 0 - q(22);
  errX(2) = 0 - q(23);
  errX(3) = 0 - q(24);
  errX(4) = 0 - q(25)
  derrX，ddxDes,dxDes = 0;

• Roll_Pitch_Yaw_Pz: 姿态高度跟踪任务
  errX(4) = 0;
  errX前3项是期望姿态误差，第4项是位置Z
  errX.block<3, 1>(0, 0) = diffRot(base_rot, desRot);
  errX(3) = base_pos_des(2) - q(2);
  derrX.block<3, 1>(0, 0) = -dq.block<3, 1>(3, 0);
  derrX(3) = 0 - dq(2);
  ddxDes， dxDes = 0；

• PxPy: 速度
  errX = Eigen::VectorXd::Zero(2);
  errX = des_dq.block(0, 0, 2, 1) * timeStep;
  derrX,ddxDes,dxDes = 0;

• PosRot: 位置位姿期望无擦痕
  errX = Eigen::VectorXd::Zero(6);
  errX.block(0,0,3,1) = base_pos_des - q.block(0,0,3,1);
  errX.block<3, 1>(3, 0) = diffRot(base_rot, desRot);
  derrX,ddxDes,dxDes = 0;

• SwingLeg: 误差是末端姿态
  errX = Eigen::VectorXd::Zero(6);
  errX.block<3, 1>(0, 0) = swing_fe_pos_des_W - fe_pos_sw_W;
  desRot = eul2Rot(swing_fe_rpy_des_W(0), swing_fe_rpy_des_W(1), swing_fe_rpy_des_W(2));
  errX.block<3, 1>(3, 0) = diffRot(fe_rot_sw_W, desRot);
  derrX,ddxDes,dxDes = 0;

• HandTrack: 误差是末端姿态
  先设定末端期望姿态和位置
  errX = Eigen::VectorXd::Zero(12);
  errX.block<3, 1>(0, 0) = hd_l_pos_W_des - hd_l_pos_cur_W;
  errX.block<3, 1>(3, 0) = diffRot(hd_l_rot_cur_W, hd_l_rot_W_des);
  errX.block<3, 1>(6, 0) = hd_r_pos_W_des - hd_r_pos_cur_W;
  diffRot(hd_r_rot_cur_W, hd_r_rot_W_des);

• HandTrackJoints：误差是末端转关节后的角度误差
  errX=resLeg.jointPosRes.block<14,1>(0,0)-q.block<14,1>(7,0);

stand:

• static_Contact：
  errX,derrX,ddxDes,dxDes,kp,kd = 0；
  taskCtMap=Eigen::MatrixXd::Zero(3,3);
  taskCtMap(0,0)=0;taskCtMap(1,1)=1;taskCtMap(2,2)=1;
  taskCtMap=fe_l_rot_cur_WtaskCtMapfe_l_rot_cur_W.transpose(); // disable ankle roll joint
  J=Jfe;
  J.block(3,0,3,model_nv)=taskCtMapJ.block(3,0,3,model_nv);
  J.block(9,0,3,model_nv)=taskCtMapJ.block(9,0,3,model_nv);
  J.block(0,22,12,3).setZero(); // exculde waist joints
  dJ读取雅可比，W = 1

• HipRPY：
  desRot = eul2Rot(0, 0, 0);
  errX.block<3, 1>(0, 0) = diffRot(hip_link_rot, desRot);
  taskMapRPY = Eigen::MatrixXd::Zero(3, 6);
  taskMapRPY(0, 3) = 1;
  taskMapRPY(1, 4) = 1;
  taskMapRPY(2, 5) = 1;
  J = taskMapRPY * J_hip_link; //髋关节雅可比矩阵
  J.block(0,22,3,3).setZero();
  J.block(0,6,3,14).setZero();

• Pz:
  errX(0) = base_pos_des(2) - q(2);
  taskMap = Eigen::MatrixXd::Zero(1, 6);
  taskMap(0, 2) = 1;
  J = taskMap * J_base;
  J.block(0,22,1,3).setZero();
  dJ = taskMap * dJ_base;
  dJ.block(0,22,1,3).setZero();

• CoMTrack:
  errX = Eigen::VectorXd::Zero(2);
  errX = pCoMDes.block(0,0,2,1)-pCoMCur.block(0,0,2,1);
  J = Jcom.block(0,0,2,model_nv);
  J.block(0,6,2,14).setZero();

• CoMXY_HipRPY: 质心xy跟踪， Hip姿态跟踪
  taskMapRPY = Eigen::MatrixXd::Zero(3, 6);
  taskMapRPY(0, 3) = 1;
  taskMapRPY(1, 4) = 1;
  taskMapRPY(2, 5) = 1;
  errX.block(0,0,2,1) = pCoMDes.block(0,0,2,1)-pCoMCur.block(0,0,2,1);
  errX.block<3, 1>(2, 0) = diffRot(hip_link_rot, desRot);
  J = Eigen::MatrixXd::Zero(5,model_nv);
  J.block(0,0,2,model_nv) = Jcom.block(0,0,2,model_nv);
  J.block(2,0,3,model_nv) = taskMapRPY * J_hip_link;
  J.block(2,22,3,3).setZero(); // exculde waist joints
  J.block(2,6,3,14).setZero(); // exculde arm joints

• HandTrackJoints: 手部跟踪
  errX=resLeg.jointPosRes.block<14,1>(0,0)-q.block<14,1>(7,0);
  J = Eigen::MatrixXd::Zero(14,model_nv);
  J.block(0,6,14,14)=Eigen::MatrixXd::Identity(14,14);

• HeadRP: 头部跟踪
  errX = Eigen::VectorXd::Zero(2);
  errX(0)=0-q(21); //头部关节
  errX(1)=base_rpy_cur(1)-q(22); //头部关节
  J = Eigen::MatrixXd::Zero(2,model_nv);
  J(0,20)=1;
  J(1,21)=1;

• Roll_Pitch_Yaw: 身体姿态跟踪
  errX = diffRot(base_rot, desRot);
  derrX = -dq.block<3, 1>(3, 0);
  taskMap = Eigen::MatrixXd::Zero(3, 6);
  taskMap(0, 3) = 1;
  taskMap(1, 4) = 1;
  taskMap(2, 5) = 1;
  J = taskMap * J_base;
  dJ = taskMap * dJ_base;

• fixedWaist： 腰部跟踪
  errX = Eigen::VectorXd::Zero(3);
  errX(0) = 0 - q(23);
  errX(1) = 0 - q(24);
  errX(2) = 0 - q(25);
  J = Eigen::MatrixXd::Zero(3, model_nv);
  J(0, 22) = 1;
  J(1, 23) = 1;
  J(2, 24) = 1;

3. 优先级多任务处理：

if (parentId==-1)
{
  taskLib[curId].N=Eigen::MatrixXd::Identity(taskLib[curId].J.cols(),taskLib[curId].J.cols());
  taskLib[curId].Jpre=taskLib[curId].J*taskLib[curId].N;
  taskLib[curId].delta_q=des_delta_q+ pseudoInv_right_weighted(taskLib[curId].Jpre,taskLib[curId].W)*taskLib[curId].errX;
  taskLib[curId].dq=des_dq;
  Eigen::VectorXd ddxcmd= taskLib[curId].ddxDes + taskLib[curId].kp * taskLib[curId].errX+taskLib[curId].kd*taskLib[curId].derrX;
  taskLib[curId].ddq= des_ddq + dyn_pseudoInv(taskLib[curId].Jpre,dyn_M_inv,true) * (ddxcmd - taskLib[curId].dJ * dq);
  std::cout<<taskLib[curId].taskName<<std::endl<<taskLib[curId].delta_q.transpose()<<std::endl;
}
else
{
  taskLib[curId].N=taskLib[parentId].N*
                    (Eigen::MatrixXd::Identity(taskLib[parentId].Jpre.cols(),taskLib[parentId].Jpre.cols())-  
                    pseudoInv_right_weighted(taskLib[parentId].Jpre,taskLib[parentId].W)*taskLib[parentId].Jpre);
  taskLib[curId].Jpre=taskLib[curId].J*taskLib[curId].N;
  taskLib[curId].delta_q=taskLib[parentId].delta_q+ pseudoInv_right_weighted(taskLib[curId].Jpre,taskLib[curId].W)*(taskLib[curId].errX-
  taskLib[curId].J*taskLib[parentId].delta_q);
  taskLib[curId].dq=taskLib[parentId].dq+ pseudoInv_right_weighted(taskLib[curId].Jpre,taskLib[curId].W)*(taskLib[curId].dxDes-
                    taskLib[curId].J*taskLib[parentId].dq);
  Eigen::VectorXd ddxcmd= taskLib[curId].ddxDes + taskLib[curId].kp * taskLib[curId].errX+taskLib[curId].kd*taskLib[curId].derrX;
  taskLib[curId].ddq= taskLib[parentId].ddq + dyn_pseudoInv(taskLib[curId].Jpre,dyn_M_inv,true) *
                                                        (ddxcmd-taskLib[curId].dJ*dq-taskLib[curId].J*taskLib[parentId].ddq);
}

第一次：
\(J_{current, pre} = J_{current}\) 雅可比
\(\Delta q_{current} = \Delta q_{des} + J_{current, pre}^{\dagger}W_{current}^{-1} * e_{current}\) 关节位置增量
\(\dot{q}_{current} = \dot{q}_{des}\) 关节速度
\(\ddot{x}_{cmd} = \ddot{x}_{des} + K_p e_{current} + K_d \dot{e}_{current}\) 任务空间加速度
\(\ddot{q}_{current} = \ddot{q}_{des} + J_{current, pre}^{\dagger} M_{inv}(\ddot{x}_{cmd} - \dot{J}_{current} \dot{q})\) 通过伪逆雅可比矩阵将任务空间的加速度ddx_com转换为关节空间的加速度，同时考虑了惯性矩阵

迭代：
\(N_{current} = N_{parent} * (I - J_{parent, pre}^{\dagger}W_{parent}^{-1} J_{parent,pre})\)
\(J_{current, pre} = J_{current} * N_{current}\) 雅可比
\(\Delta q_{current} = \Delta q_{parent} + J_{current, pre}^{\dagger}W_{current}^{-1} * (e_{current} - J_{current} \Delta q_{parent})\) 关节位置增量
\(\dot{q}_{current} = \dot{q}_{parent} + J_{current, pre}^{\dagger}W_{current}^{-1}(\dot{x}_{des} - J_{current} \dot{q}_{parent})\) 关节速度
\(\ddot{x}_{cmd} = \ddot{x}_{des} + K_p e_{current} + K_d \dot{e}_{current}\) 任务空间加速度
\(\ddot{q}_{current} = \ddot{q}_{parent} + J_{current, pre}^{\dagger} M_{inv}(\ddot{x}_{cmd} - \dot{J}_{current} \dot{q} - J_{current} \ddot{q}_{parent})\)

4. QP问题：

• \(\ddot{q}^{cmd}:\)由上面优先级多任务处理计算
• \(f^{MPC}_r:\)由MPC获取
• \(\delta_f:\)浮动基座加速度松弛变量
• \(\delta_{f_r}:\)接触力松弛变量
  QP问题就是根据动力学等式约束，来求解这两个最优的松弛变量
  松弛变量求解出来后，\(\ddot{q}\)和\(f_r\)也出来了。
  然后根据动力学方程，求解各个关节的力矩：
  
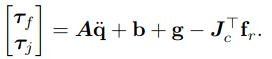
  \(\tau_j\)即为关节力矩

void WBC_priority::computeTau()
{
  eigen_qp_A1 = Zero(6, 18); //18 means the sum of dims of delta_r and delta_Fr

  St_qpV1 = (37, 6)
  St_qpV1.block<6, 6>(0, 0) = Eigen::MatrixXd::Identity(6, 6);

  //sf是6维浮动动力学选择矩阵
  Sf = Eigen::MatrixXd::Zero(6, 37);
  Sf.block<6, 6>(0, 0) = Eigen::MatrixXd::Identity(6, 6);

  eigen_qp_A1.block<6, 6>(0, 0) = Sf * dyn_M * St_qpV1;
  eigen_qp_A1.block<6, 12>(0, 6) = -Sf * Jfe.transpose(); //Jfe是足末端雅可比 

  Eigen::VectorXd eqRes = Eigen::VectorXd::Zero(6);
  //动力学平衡方程等式约束，这里还没有加上松弛变量，ddq_final_kin由多任务所得关节加速度，Fr_ff是由MPC所得
  eqRes = -Sf * dyn_M * ddq_final_kin - Sf * dyn_Non + Sf * Jfe.transpose() * Fr_ff;
  
  //x是由浮动基座加速度松弛变量（前6维）和接触力松弛变量（后12维）
  // obj: (1/2)x'Hx+x'g
  // s.t. lbA<=Ax<=ubA
  //       lb<=x<=ub
  //H的权重矩阵
  eigen_qp_H.block<6, 6>(0, 0) = Q2 * 2.0 * 1e7;
  eigen_qp_H.block<12, 12>(6, 6) = Q1 * 2.0 * 1e1;
  //由QP问题构造可知，g = 0
  //主要问题由A和lbA,ubA构成，lbA,ubA相等的项为等式约束，不相等的项为不等式约束
  //下面主要分析A和lbA,ubA
  eigen_qp_A_final = Zero(22, 6+12);
  eigen_qp_A_final.block<6, 18>(0, 0) = eigen_qp_A1;
  eigen_qp_A_final.block<16, 18>(6, 0) = eigen_qp_A2;
  eigen_qp_A2.block<16, 12>(0, 6) = W;
  neqRes_low = f_low - W * Fr_ff;
  neqRes_upp = f_upp - W * Fr_ff;
  eigen_qp_lbA.block<6, 1>(0, 0) = eqRes;
  eigen_qp_lbA.block<16, 1>(6, 0) = neqRes_low;
  eigen_qp_ubA.block<6, 1>(0, 0) = eqRes;
  eigen_qp_ubA.block<16, 1>(6, 0) = neqRes_upp;
  res = QP_prob.init(qp_H, qp_g, qp_A, NULL, NULL, qp_lbA, qp_ubA, nWSR, &cpu_time, xOpt_iniGuess);
  
  //获取最优解
  QP_prob.getPrimalSolution(xOpt);
  //加上松弛变量
  eigen_ddq_Opt = ddq_final_kin;
  eigen_ddq_Opt.block<6, 1>(0, 0) += eigen_xOpt.block<6, 1>(0, 0);
  eigen_fr_Opt = Fr_ff + eigen_xOpt.block<12, 1>(6, 0);

  //根据全身动力学计算关节力矩
  tauRes = dyn_M * eigen_ddq_Opt + dyn_Non - Jfe.transpose() * eigen_fr_Opt;
}