青龙源码解析MPC
1. 全身运动学
青龙全身共31个自由度。
2个7自由度臂,2个头部自由度,3个腰部自由度,每个腿是6个自由度(髋关节3DOF,膝关节1DOF,踝关节2DOF)
共7+7+2+3+6+6=31
再加上浮动基座6自由度,总共37自由度。
2. 变量:
输入:13 * 3 = 39的纬度;约束:32 * 3的纬度
-
Ac,Bc,A,B,Cc,C: 状态空间矩阵
Ac,A: [12, 12]
Bc,B: [12, 13]
Cc,C: [12,1] -
Aqp,bqp,cqp: QP问题的约束矩阵
Aqp: [120,12]
Aqp1: [120,120]
Bqp1: [120,130]
Bqp: [120.39]
Cqp1: [120,1]
Cqp: [120,1] -
Ufe,Ufe_pre,xd,X_cur,X_cal,dX_cal: 输入,状态
Ufe: [39,1] 输入 13 * 3
Ufe_pre: [13,1]
Xd: [120,1]
X_cur: [12,1]
X_cal: [12,1]
dX_cal: [12,1] -
L,K,M,alpha,H,c: QP相关矩阵
L: [120,120] 优化变量状态权重(欧拉角,位置,角速度,速度)
K: [39,39] 优化变量输入权重(接触力)
M: [39,39]
H: [39,39]
c: [39,1] -
u_low,u_up,As,bs: 输入约束,约束矩阵
u_low,u_up: [39,1]
As: [96,39]
bs: [96,1]
3. MPC::cal()
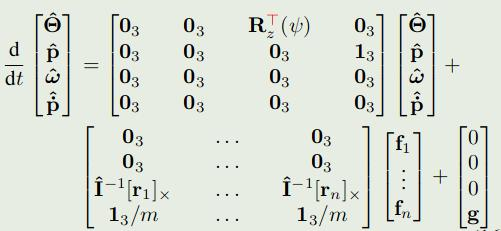



1. 这段代码,Aqp1计算了A的迭代矩阵,10步是[120, 120]
for (int i = 0; i < mpc_N; i++)
{
Ac[i].block<3, 3>(0, 6) = R_curz[i].transpose();
Ac[i].block<3, 3>(3, 9) = Eigen::MatrixXd::Identity(3,3);
A[i] = Eigen::MatrixXd::Identity(nx,nx) + dt * Ac[i];
}
for (int i = 0; i < mpc_N; i++)
Aqp.block<nx, nx>(i * nx, 0) = Eigen::MatrixXd::Identity(nx,nx);
for (int i = 0; i < mpc_N; i++)
for (int j = 0; j < i + 1; j++)
Aqp.block<nx, nx>(i * nx, 0) = A[j] * Aqp.block<nx, nx>(i * nx, 0);
for (int i = 0; i < mpc_N; i++)
for (int j = 0; j < i + 1; j++)
Aqp1.block<nx, nx>(i * nx, j * nx) = Eigen::MatrixXd::Identity(nx,nx);
for (int i = 1; i < mpc_N; i++)
for (int j = 0; j < i; j++)
for (int k = j + 1; k < (i + 1); k++)
Aqp1.block<nx, nx>(i * nx, j * nx) = A[k] * Aqp1.block<nx, nx>(i * nx, j * nx);
2. 这代代码,Bqp计算了B的迭代矩阵,注意与上图\(u_i\)不同的是,该程序的u为:\([m_0, f_0, m_1, f_1]\),先左腿;
另外,姿态和位置只用了速度积分,并没有用到加速度积分
这里注意Bqp1到B_tmp的转换?
这里给我的感觉是MPC主要跟踪状态,输入不需要跟踪,所以跟踪10步的状态,输入u产生3步的预测,最终也只会用到第一个u,这么处理减小矩阵运算???

for (int i = 0; i < mpc_N; i++)
Bqp1.block<nx, nu>(i * nx, i * nu) = B[i];
Eigen::MatrixXd Bqp11 = Eigen::MatrixXd::Zero(nu * mpc_N, nu * ch);
Bqp11.setZero();
Bqp11.block<nu * ch, nu * ch>(0, 0) = Eigen::MatrixXd::Identity(nu * ch, nu * ch);
for (int i = 0; i < (mpc_N - ch); i++)
Bqp11.block<nu, nu>(nu * ch + i * nu, nu * (ch - 1)) = Eigen::MatrixXd::Identity(nu, nu);
Eigen::MatrixXd B_tmp = Eigen::MatrixXd::Zero(nx * mpc_N, nu * ch);
B_tmp = Bqp1 * Bqp11;
Bqp = Aqp1 * B_tmp;
3. 这段代码,根据不同的摆动腿,增加重力加速度,先左腿后右腿
Eigen::Matrix<double, nu*ch, 1> delta_U;
delta_U.setZero();
for (int i = 0; i < ch; i++){
if (legState[i] == DataBus::LSt)
delta_U(nu*i + 2) = m*g;
else if (legState[i] == DataBus::RSt)
delta_U(nu*i + 8) = m*g;
else{
delta_U(nu*i + 2) = 0.5*m*g;
delta_U(nu*i + 8) = 0.5*m*g;
}
}
4. 构建QP的矩阵:
H = 2 * (Bqp.transpose() * L * Bqp + alpha * K) + 1e-10*Eigen::MatrixXd::Identity(nx*mpc_N, nx*mpc_N);
c = 2 * Bqp.transpose() * L * (Aqp * X_cur - Xd) + 2 * alpha * K * delta_U;
5. 摩擦锥约束:

这里跟公式略有出入,但大差不差,约束的效果是产生的力尽量保持垂直
//friction constraint
Eigen::Matrix<double, ncfr_single, 3> Asfr111, Asfr11;
Eigen::Matrix<double, ncfr, nu> Asfr1;
Eigen::Matrix<double, ncfr * ch, nu * ch> Asfr;
Asfr111.setZero();
Asfr1.setZero();
Asfr.setZero();
Asfr111 <<
-1.0, 0.0, -1.0 / sqrt(2.0) * miu,
1.0, 0.0, -1.0 / sqrt(2.0) * miu,
0.0, -1.0, -1.0 / sqrt(2.0) * miu,
0.0, 1.0, -1.0 / sqrt(2.0) * miu;
Asfr11 = Asfr111 * R_w2f;
Asfr1.block<ncfr_single, 3>(0, 0) = Asfr11;
Asfr1.block<ncfr_single, 3>(ncfr_single, 6) = Asfr11;
for (int i = 0; i < ch; i++)
Asfr.block<ncfr, nu>(ncfr * i, i * nu) = Asfr1;
Asfr是24*39的矩阵。最小值:-1e7,最大值根据双腿状态,哪个腿站立,哪个腿为0,双腿都站,都为0。意思是那条腿站立,那条腿进行约束
6. 水平方向力矩等效点不要超过足底多边形,ZMP?:
力矩等效点:\(M_xy = r_{xy} \times f_{xy} <= 足底多边形\)
//moment constraint x y
double sign_xy[4]{1.0, -1.0, -1.0, 1.0};
Eigen::Matrix<double, 3, 1> gxyz[4];
gxyz[0] << 0.0, 1.0, 0.0;
gxyz[1] << 0.0, 1.0, 0.0;
gxyz[2] << 1.0, 0.0, 0.0;
gxyz[3] << 1.0, 0.0, 0.0;
Eigen::Matrix<double, 3, 1> r[4];
Eigen::Matrix<double, 3, 1> p[4];
Eigen::Matrix<double, ncstxya, 6> Astxy_r[4];
Eigen::Matrix<double, ncstxy_single, 6> Astxy11;
Eigen::Matrix<double, ncstxy, nu> Astxy1;
Eigen::Matrix<double, ncstxy * ch, nu * ch> Astxy;
Astxy_r[0].setZero();
Astxy_r[1].setZero();
Astxy_r[2].setZero();
Astxy_r[3].setZero();
Astxy11.setZero();
Astxy1.setZero();
Astxy.setZero();
r[0] << 0.0, 1.0, 0.0;
r[1] << 0.0, 1.0, 0.0;
r[2] << 1.0, 0.0, 0.0;
r[3] << 1.0, 0.0, 0.0;
p[0] << delta_foot[0], 0.0, 0.0;
p[1] << -delta_foot[1], 0.0, 0.0;
p[2] << 0.0, delta_foot[2], 0.0;
p[3] << 0.0, -delta_foot[3], 0.0;
for (int i = 0; i < 4; i++) {
Astxy_r[i].block<1, 3>(0, 0) =
sign_xy[i] * gxyz[i].transpose() * R_w2f * R_f2w * r[i] * (R_f2w * r[i]).transpose() *
CrossProduct_A(R_f2w * p[i]);
Astxy_r[i].block<1, 3>(0, 3) = sign_xy[i] * gxyz[i].transpose() * R_w2f;
Astxy11.block<ncstxya, 6>(i * ncstxya, 0) = Astxy_r[i];
}
Astxy1.block<ncstxy_single, 6>(0, 0) = Astxy11;
Astxy1.block<ncstxy_single, 6>(ncstxy_single, 6) = Astxy11;
for (int i = 0; i < ch; i++)
Astxy.block<ncstxy, nu>(ncstxy * i, nu * i) = Astxy1;
7. 垂直方向力矩等效点不要超过足底多边形,ZMP?
循环计算每个腿4个接触点与Z方向相关的力矩
for (int i = 0; i < 4; i++) {
Astz_r[i].block<1, 3>(0, 0) = -sqrt(p[i](0) * p[i](0) + p[i](1) * p[i](1) + p[i](2) * p[i](2)) * miu *
Eigen::Matrix<double, 1, 3>(0.0, 0.0, 1.0) * R_w2f;
Astz_r[i].block<1, 3>(0, 3) = Eigen::Matrix<double, 1, 3>(0.0, 0.0, 1.0) * R_w2f;
Astz_r[i].block<1, 3>(1, 0) = Astz_r[i].block<1, 3>(0, 0);
Astz_r[i].block<1, 3>(1, 3) = -1*Astz_r[i].block<1, 3>(0, 3);
Astz11.block<ncstza, 6>(i * ncstza, 0) = Astz_r[i];
}
Astz1.block<ncstz_single, 6>(0, 0) = Astz11;
Astz1.block<ncstz_single, 6>(ncstz_single, 6) = Astz11;
for (int i = 0; i < ch; i++)
Astz.block<ncstz, nu>(ncstz * i, nu * i) = Astz1;
8. QP初始化:
res = QP.init(qp_H, qp_c, qp_As, qp_lu, qp_uu, qp_lbA, qp_ubA, nWSR, &cpu_time, xOpt_iniGuess);
qp_H,qp_c:QP目标函数
qp_As:约束矩阵
qp_lu, qp_uu:变量上下界,lu <= x <= uu
qp_lbA, qp_ubA: 约束边界,lbA <= A * x <= ubA; 如果lbA和ubA相等,就是等式约束
nWSR: 输入工作集重新计算次数,输出实际
cpu_time:输入允许QP初始化的最大时间,输出实际时间
xOpt_iniGuess:初值猜想
9. 结果计算:
dX_cal计算\(\dot{x} = Ax + Bu\)
delta_X根据\(\dot{x}\)进行加速度积分,得到这个控制周期的状态增量
X_cal根据离散状态方程,计算最优控制下,当前的状态。
Ufe_pre是最优控制的第一个点,也会用到WBC中
dX_cal = Ac[0] * X_cur + Bc[0] * Ufe.block<nu,1>(0,0);
Eigen::Matrix<double, nx, 1> delta_X;
delta_X.setZero();
for (int i = 0; i < 3; i++){
delta_X(i) = 0.5*dX_cal(i+6)*dt*dt;
delta_X(i+3) = 0.5*dX_cal(i+9)*dt*dt;
delta_X(i+6) = dX_cal(i+6)*dt;
delta_X(i+9) = dX_cal(i+9)*dt;
}
X_cal = (Aqp * X_cur + Bqp * Ufe).block<nx,1>(nx*0,0) + delta_X;
Ufe_pre = Ufe.block<nu, 1>(0, 0);



