Dynamic Locomotion in the MIT Cheetah 3 Through Convex Model-Predictive Control

1. Swing Leg Control

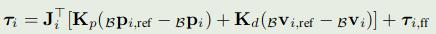
\(J_i \in R^{3*3}\) 是足端雅可比；\(\tau _{i,ff}\) 是前馈力矩
\(\Lambda \in R^{3*3}\)是操作空间惯性矩阵；\(a_{i,ref} \in R^{3*3}\)是机体坐标系下的参考加速度
q是关节角度；\(C_i \dot{q}_i + G_i\)是科里奥利力和重力

2. Ground Force Control

\(\tau_i = J_i^T R_i^T f_i\)
\(R^T\)世界坐标转机体坐标；\(J_i \in R^{3*3}\) 是足端雅可比；f是MPC求出的接触力

3. 单刚体动力学：

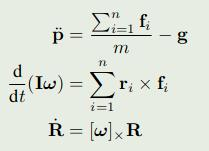
3.1 角速度近似

机体到世界坐标的转换：\(R = R_z(\psi) R_y(\theta) R_x(\phi)\)
\(\psi\)：yaw;
\(\theta\): pitch;
\(\phi\): roll
考虑pitch和roll都比较小，近似为0处理：


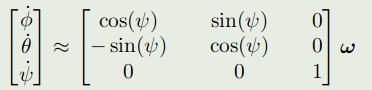
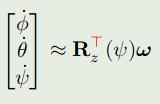
这里注意欧拉角的先后顺序。

3.2 角惯性近似：

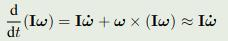
小角速度的时候，第二项很小，不考虑

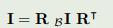
考虑比较小的roll和pitch，不考虑

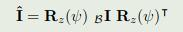
4.简化的动力学：

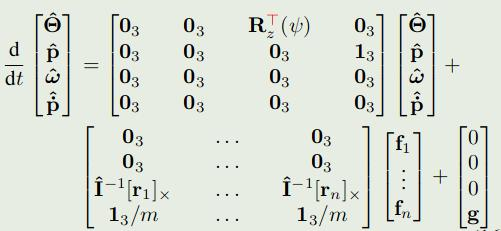
可以写成：\(\dot{x}(t) = A_c(\psi)x(t) + B_c(r_1, ...,r_n, \psi) u(t)\)

5.线性离散：

将\(B_c\)在参考轨迹下的\(\psi, r_i\)进行近似展开，\(A\)在参考轨迹下的\(\psi\)近似展开。
下面给出一个例子：

简单的解释：
下一时刻位置 = 当前位置 + 速度 * t + 1/2 * 加速度 * \(t^2\)
速度 = 当前速度 + 当前加速度 * t + 输入加速度 * t

6. MPC