题解-拉格朗日（bzoj3695变种）

Problem

在无穷大的水平面上有一个平面直角坐标系，\(N-1\)条垂直于\(x\)轴的直线将空间分为了\(N\)个区域

你被要求把\((0,0)\)处的箱子匀速推到\((x,y)\)

箱子受水平面的摩擦力与正压力正相关，所以在第\(i\)个区域的摩擦力可以表示为\(f_i\)

求把箱子推到目的地做的最小功是多少呢？(不考虑改变速度时的做功)

\(N\leq 100\)

Thoughts

这道题看题面是物理题，但一般来说这些题都是借着物理题的外表掩饰自己的数学本质

以为要从两块区域的简单情形入手，但我发现自己连两块区域都不会做；想到如果所有的\(f_i\)都相等的话，那么只要连一条直线即可，那么想法儿把\(f_i\)化进去，但发现\(\sqrt {x^2+y^2}\)的式子好像没法把\(f_i\)的系数化进去

转念一想，发现箱子肯定在\(f_i\)更大的地方移动得越少，而且在同一块区域内肯定是走直线，所以两块区域中的直线在交界的地方肯定有一个角度偏差，即箱子的整条移动路径是一条折线段

马上可以联想到光在不同介质交界处的折射现象

Physics

既然我们要利用折射计算精确值，那么我们就不能像初中那样仅仅掌握判断入射角和折射角大小关系的方法，我们需要定量计算！

惠更斯原理

惠更斯原理是指球形波面上的每一点（面源）都是一个次级球面波的子波源，子波的波速与频率等于初级波的波速和频率，此后每一时刻的子波波面的包络就是该时刻总的波动的波面。其核心思想是：介质中任一处的波动状态是由各处的波动决定的

看下面几幅图片基本就能理解

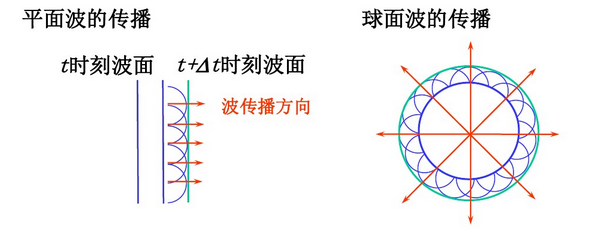
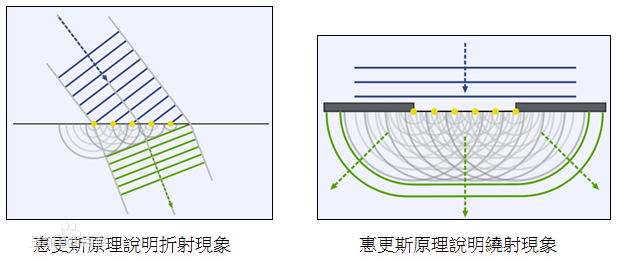
（图引自百度）

折射

有了这个原理，我们来证明一个定量的折射定理，如下图

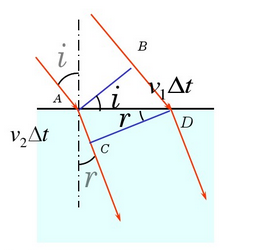
光线在同一时间于\(A,B\)两点处放出子波源，在一个极短的时间\(\Delta t\)内，\(A\)放出的子波源到达\(C\)点，\(B\)放出的子波源到达\(D\)，则有

\[\left . \begin{matrix} \sin i=\frac {\Delta tv_1}{AD}\\ \sin r=\frac {\Delta tv_2}{AD}\\ \end{matrix} \right\}\Rightarrow \frac {\sin i}{\sin r}=\frac {v_1}{v_2} \]

Solution

如何将上面的式子进行应用呢，由于并不是\(f_i\)越大答案越优，所以我们可以取\(v_i=\frac 1{f_i}\)，则我们可以得到任意相邻两区间直线斜率的关系：

\[\frac {\sin \theta_1}{\sin \theta_2}=\frac {f_2}{f_1} \]

但我们并不知道任何区间的斜率，所以我们可以设第一个区间的斜率为\(\theta_0\)（即从原点射出的第一条线段），并且考虑到这条折线在结束横坐标\(x\)的纵坐标\(y_0\)是关于\(\theta_0\)单调递增的，所以我们可以二分\(\theta_0\)来逼近最终我们的期望结束纵坐标\(y\)，而我们要求答案的最小值，则我们只有当\(y_0\geq y\)时才能更新答案

……当我们开开心心打完代码，会发现连第二个样例都过不了，交上去只有\(20∽30\)分，问题出在哪了？

容易想到 调试发现 由于我们是以\(\sin \theta\)为途径转移，而途中我们的\(\sin \theta\)可能会出现大于\(1\)的情况，而这种情况的发生是并不是因为发生了全反射，而是我们设的初始值\(\theta_0\)不合法，我们要求\(\forall i\in [1,n],\sin \theta \in [-1,1]\)，而\(\sin \theta =\sin \theta_0\frac {f_1}{f_i}\)

所以我们需要设定二分的上界\(\sin \theta_0\leq \frac {\min\{f_i\}}{f1}\)，至此此题解决

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rg register
#define pi (3.14159265358979323846)

const int N=110;
const double eps=1e-8;
double x[N],f[N];
double ans=1e20,Y;
int n;

inline int calc(double theta){
	double y=0.0,yy,res=0.0;
	theta=sin(theta);
	for(rg int i=1;i<=n;++i){
		yy=x[i]*tan(asin(theta));
		theta*=f[i]/f[i+1];
		res+=sqrt(x[i]*x[i]+yy*yy)*f[i];
		y+=yy;
	}
	if(y>Y)
	ans=fmin(ans,res);
	return y>Y;
}

int main(){
	scanf("%d",&n);
	double l=0.0,r=pi*0.5,m,mi=1e20;
	for(rg int i=1;i<=n;++i){
		scanf("%lf%lf",&x[i],&f[i]);
		if(i^1)mi=fmin(mi,f[i]);
	}
	scanf("%lf",&Y);
	r=min(r,asin(mi/f[1]));
	while(l+eps<r){
		m=(l+r)*0.5;
		if(calc(m))r=m;
		else l=m;
	}printf("%.3lf\n",ans);
	return 0;
}