笔记-几何法解决三点定圆问题
Problem
题意概要：给定平面上\(n\)个点，求覆盖所有点的最小圆
Solution
刚看到这道题很迷，感觉感觉要\(O(n^3)\)，但看了wwt的讲解，发现这题可以做到期望\(O(n)\)，题解就不写了，网上到处都是（这篇比较明晰）
这里主要讲一下如何根据三点求过这三点的圆的问题
网上好像都是在解方程？
dalao代码：
if(fabs(a[j].y-a[i].y)<=eps||fabs(a[k].y-a[i].y)<=eps) continue;
l1.k=-(a[j].x-a[i].x)/(a[j].y-a[i].y);
l1.b=(a[i].y+a[j].y)/2-l1.k*(a[i].x+a[j].x)/2;
l2.k=-(a[k].x-a[i].x)/(a[k].y-a[i].y);
l2.b=(a[i].y+a[k].y)/2-l2.k*(a[i].x+a[k].x)/2;
if(fabs(l1.k-l2.k)<=eps) continue;
o=intersection(l1,l2);r=o.dis(a[i]);
我用的向量＋几何方法，而这种做法的核心代码很短 其实也没短到哪里去
pnt b1=(p0+p1)*0.5,b2=(p0+p2)*0.5,d1=p1-p0,d2=p2-p0;
d1.rev(),d2.rev();
return b1+d1*(((b1-b2)*d2)/(d2*d1));
但不用特判斜率啊，下面证明一下（下面的线段长度就直接写线段名啦）
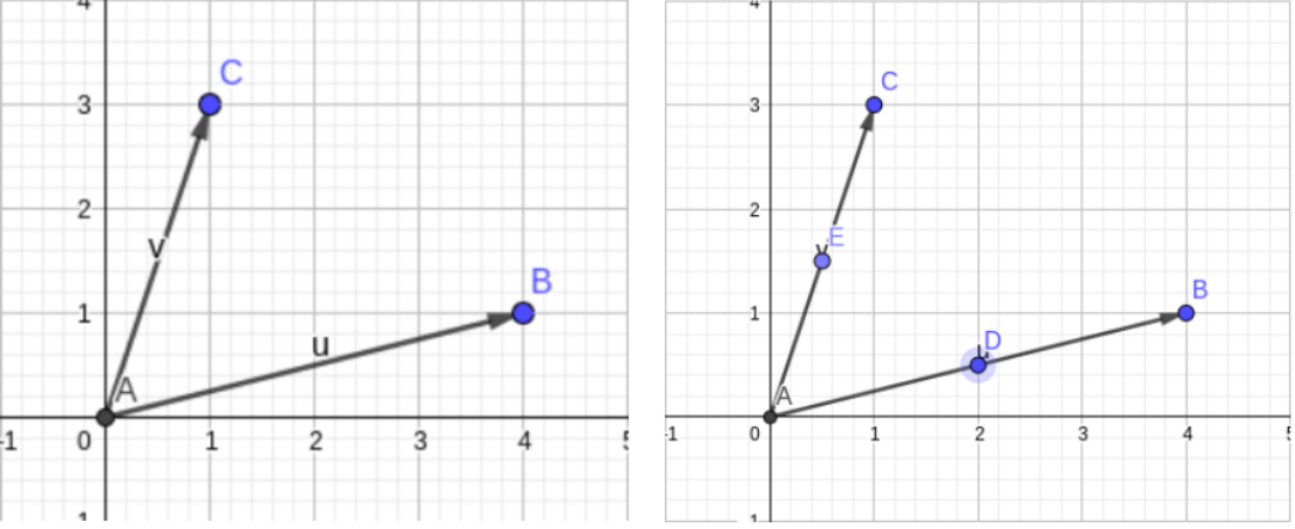
先画一个三角形\(\triangle ABC\)，简化一下，以\(A\)为原点，画两个向量\(\vec {AB},\vec{AC}\)（图一）
然后由于\(\triangle ABC\)的外接圆圆心在三角形三条中垂线交点处，取得\(AB,AC\)中点\(D,E\)（图二）
再做出中垂线\(DF,EG\)，注意这里不会直接做出中垂线，取而代之旋转向量，设\(A\)为旋转中心，将\(AB\)旋转\(90°\)为\(AH\)，同理\(AC\)得\(AI\)，这个是可以用复数旋转出来的，但由于这个角是直角，所以可以特别判断，向量\((x,y)\)变为\((-y,x)\)
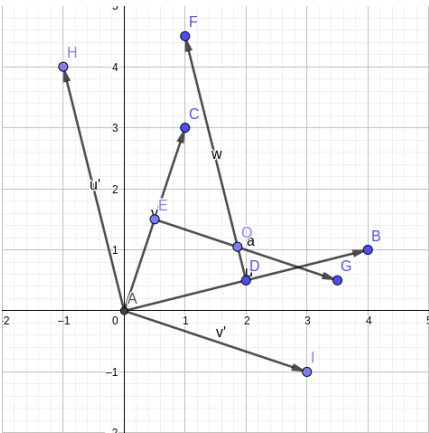
发现这时\(\vec{DF}\)与\(\vec{EG}\)的交点就是要求的圆心坐标，不妨设为\(O\)，这会儿需要得到\(O\)的坐标，即向量\(\vec {AO}\)，考虑到\(\vec {AO}=\vec {AE}+\vec {EO}\)，而已经知道\(\vec {AE}=\frac 12 \vec {AC}\)，所以只用求\(\vec {EO}\)
再考虑到已知条件中仅有\(\vec {AI}=\vec {EG}\)是与之相关的，即\(EO=k\cdot \vec {EG}=k\cdot \vec {AI}\)，要求出这个比值\(k\)
连接\(EF,DE,HI\)，再过\(I\)作\(IJ \perp AB\)，过\(E\)作\(EK \perp DF\)
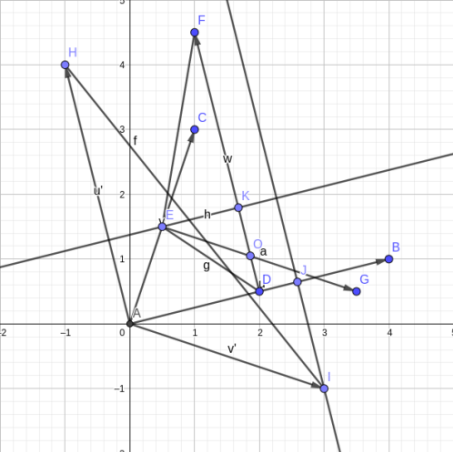
这时做出了两个三角形\(\triangle AHI,\triangle EFD\)，\(S_{\triangle AHI}=\frac 12AH\cdot AJ,S_{\triangle EFD}=\frac 12DF\cdot EK\)，因为\(AH=ED\)，所以\(\frac {EK}{AJ}=\frac{S_{\triangle AHI}}{S_{\triangle EFD}}\)
根据多年初中数学直觉，发现\(\triangle EKO∽ \triangle AJI\)，理由是三条边分别平行，则三个角对应相等，根据上面的那个等式 ，发现\(k=\frac {EO}{AI}=\frac {EK}{AJ}=\frac{S_{\triangle AHI}}{S_{\triangle EFD}}\)，而\(S_{\triangle AHI}=\frac 12 \vec{AH}×\vec{AI},S_{\triangle EFD}=\frac 12 \vec{DE}×\vec{DF}=\frac 12 (\vec{AE}-\vec{AD})×\vec{AH}\)
则
\(\vec {AO}\\=\vec {AE}+\vec {EO}\\=\vec {AE}+k\cdot \vec {AI}\\=\frac {EO}{AI}\cdot \vec {AI}\\=\frac {EK}{AJ}\cdot \vec {AI}\\=\frac{S_{\triangle AHI}}{S_{\triangle EFD}}\cdot \vec {AI}\\=\frac{\vec{AH}×\vec{AI}}{ (\vec{AE}-\vec{AD})×\vec{AH}}\cdot \vec {AI}\)
到此，以上\(\vec {AH},\vec {AI},\vec {AE},\vec {AD}\)都是已知量，\(\vec {AE},\vec {AD}\)为原来三角形中向量的一半，\(\vec {AH} , \vec {AI}\)为旋转后的向量
由此可知，只需要将两个向量旋转\(90°\)，求两个叉积就可以根据给定的三个点求过这三个点的圆心
upd：现在回看这个做法感觉有些智障
