题解-AtCoder Code-Festival2017qualA-E Modern Painting
Problem
题意:有一个\(n\)行\(m\)列的方格,在边界外有可能有机器人(坐标为\((0,x),(n+1,x),(x,0),(x,m+1)\),机器人方向朝内(也就是左边界外的机器人朝右,上边界外的机器人朝内……),机器人有自己独特的颜色(没有两个机器人颜色相同)。
给机器人安排一个出发顺序,机器人将依次出发,对于每个机器人,走过的路上会留下自己的颜色,它将继续前进除非出了另一方的边界或遇到了其他机器人留下的颜色。求有多少种最终状态(即方格染色情况不同)
\(n,m\leq 10^5\)
输入是给出每个边界外是否有机器人,即机器人数量不超过\(2(n+m)\leq 4\times 10^5\)
Solution
想了半天未果,然后看到题解的图恍然大悟
情况太复杂,考虑简化版的情况:先考虑只有一个角或半平面的情况
若棋盘只有一个角(角块)
可假定机器人仅从上、左出发,设有\(n\)行\(m\)列,共\(n+m\)个机器人
先画出一个\(n\)行\(m\)列的方格,共有\(nm\)个交点,随意画出一种结果,发现如果始终沿着最内侧线走,并在最下边和最右边加限制边,可以得到下面这张图(图中红色路径):
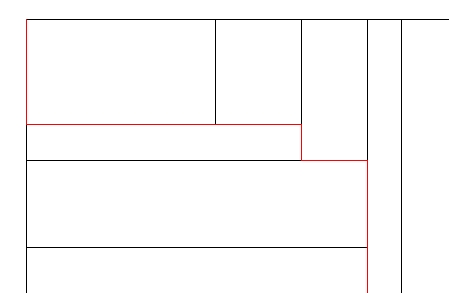
此时发现其中的红色路径依次穿过了\(n+m\)条直线(尽管有的没和线段相交,但和延长线相交),而实际上整张图最终的状态也只会和这个穿过的顺序有关
由于穿过\(n\)条横线的顺序是固定的,穿过\(m\)条横线的顺序也是固定的,所以这个状态数相当于找\(n\)个黑球和\(m\)个白球排成一列的不同方案数,由组合知识可知方案数为\(\binom {n+m}n\)
若棋盘只有一个半平面
可假定机器人从上、左、右出发
利用上面的思想:若第一个机器人是上下移动的,则会将这个状态化为一个子问题;若第一个机器人是从左往右的,则会将这个状态划分为两个角的情况(也就是上面说的)
这样就能简单地推广到全平面问题了:第一个机器人将局面划分为两个半平面
然后经过思考得知,这样复杂度为\(O(nm)\),虽然通过不了此题,但若是在\(OI\)赛制的考试中,就能与别人拉开巨大的差距
对称思想
上面的做法是通过不了此题的,思考半天也没发现可以利用组合数公式优化 然后就翻开了罪恶的题解……
先放一张题解的图
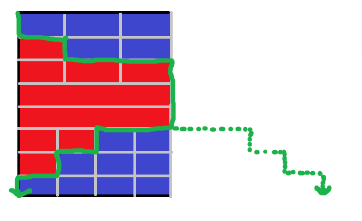
之前在四分之一角那一块中提到的红线,在官方题解里它是一个红色区域
- 在角中红色区域是一个单调的阶梯状是因为只有上面和左边的机器人
- 考虑到在半平面情况中,还存在下边的机器人,所以红色区域为一个单峰的阶梯状
如果利用之前角块的思想解半平面,可以利用图中所给的对称轴,将单峰的阶梯对称为单调的阶梯……然后就能用角块的公式来解半平面了!
列下公式:若左边有\(n\)个机器人,上面和下面共有\(m\)个机器人,则答案为\(\binom {n+m}n-\binom {n+m-1}n=\binom {n+m-1}{n-1}\)(之所以要减去是因为至少要沿着对称轴走一次才能保证对称的正确性)
汇总
然后就可以枚举第一只机器人如何划开平面将其划分为半平面的,假设第一只机器人是走竖直线段
相应的,由于不好处理半平面中“一只机器人走完仍然是一个半平面”的问题,所以可以枚举不会出现这种状态的左右边界,然后这个枚举可以用前缀和优化成\(O(n)\)
特判
- 注意第一只机器人的走向可能是横向,也可能是纵向
- 注意组合数部分不要爆负
- 注意若同一列(行)若有上下两个机器人,且这两个机器人之间没有障碍,需要将答案乘以2(因为可以上面先走或下面先走)
- 若根本没有机器人,应该输出1
Code
再不懂就看代码吧
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=101009,p=998244353,inv2=p+1>>1;
char A[N],B[N],C[N],D[N];
int fac[N<<2],inv[N<<2];
int n,m,ans;
inline int qpow(int A,int B){
int res(1);while(B){
if(B&1)res=(ll)res*A%p;
A=(ll)A*A%p,B>>=1;
}return res;
}
inline int Com(int nn,int mm){return (ll)fac[nn]*inv[mm]%p*inv[nn-mm]%p;}
void prework(int A){
fac[0]=inv[0]=1;
for(int i=1;i<=A;++i)fac[i]=(ll)fac[i-1]*i%p;
inv[A]=qpow(fac[A],p-2);
for(int i=A-1;i;--i)inv[i]=(ll)inv[i+1]*(i+1)%p;
}
void work(){
int left=0,right=0,l=0,r=0,pre=1,val;
for(int i=1;i<=n;++i)left+=A[i]-'0',right+=B[i]-'0';
for(int i=m;i;--i)r+=C[i]-'0'+D[i]-'0';
for(int i=1;i<=m;i++){
l+=C[i]-'0'+D[i]-'0';
r-=C[i]-'0'+D[i]-'0';
if(C[i]=='0' and D[i]=='0')continue;
if(C[i]=='1' and D[i]=='1')pre=2ll*pre%p;
if(right)val=Com(right+r-1,r);
else val=(!r); ans=(ans+(ll)pre*val)%p;
if(left)val=Com(left+l-1,l);
else val=(!l); pre=(pre+val)%p;
}
}
int main(){
scanf("%d%d",&n,&m);
prework(n+m+n+m);
scanf("%s%s",A+1,B+1);
scanf("%s%s",C+1,D+1);
bool died=true;
for(int i=1;i<=n;++i)
if(A[i]=='1' or B[i]=='1' or C[i]=='1' or D[i]=='1')
{died=false;break;}
if(died){puts("1");return 0;}
work();
swap(n,m);swap(A,C);
swap(B,D);swap(C,D);
work();
printf("%d\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号