风控领域常用评估指标:ROC/AUC、KS、Gain、Lift等
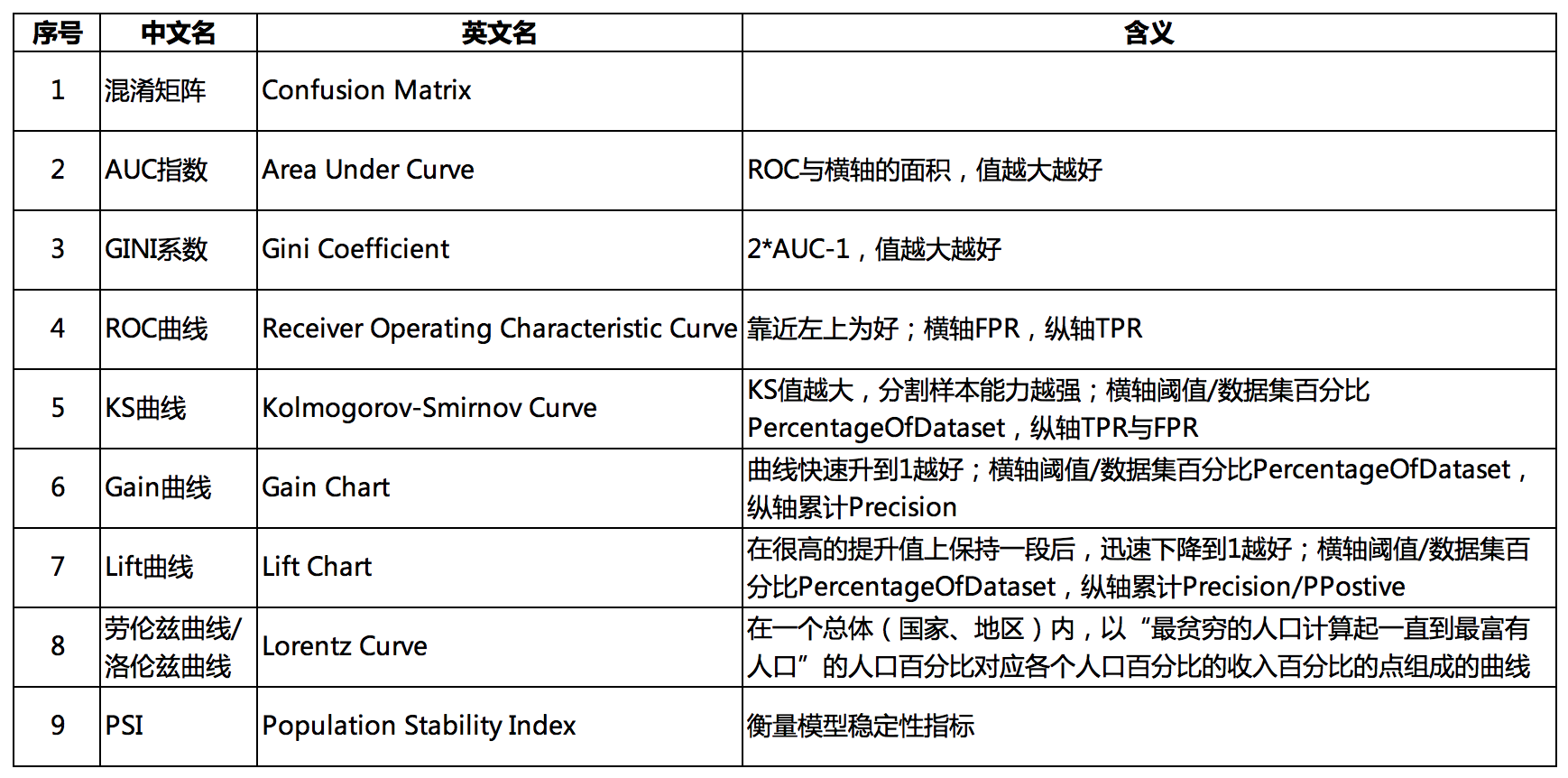
混淆矩阵
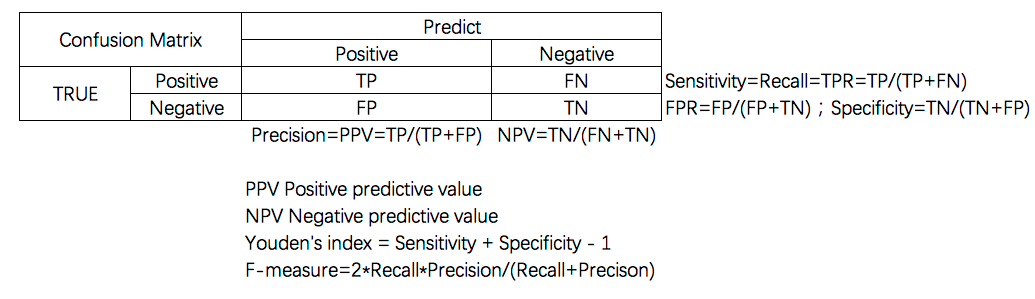
KS曲线与ROC曲线
KS曲线
KS检验:比较频率分布\(f(x)\)与理论分布\(g(x)\)或两个观测值分布的是否一致检验方法,原假设两个数据分布一致或数据符合理论分布,统计量\(D=max|f(x)-g(x)|\)
KS值计算步骤:
- 对变量进行分箱binning,可以选择等频、等距或自定义距离;
- 计算每个分箱区间的好账户数Goods与坏账户数Bads;
- 计算每个分箱区间: (累计好账户数/总好账户数) Good%、(累计坏账户数/总坏账户数) Bad%;
- 每个评分区间: abs(累计好账户占比-累计坏账户占比) abs(累计Good%-累计Bad%);
- max{abs(累计Good%-累计Bad%)}即为评分卡的KS值。
KS曲线绘制步骤:
- 将预测出的正例概率结果从大到小排序;
- 按顺序选取截断点,并计算TPR与FPR;
- 横轴为样本的占比百分比(最大100%),纵轴分别为TPR与FPR,即得到KS曲线;
- TPR与FPR曲线最大间隔距离就是KS值。
设\(f(s|P)\)为正样本预测值的累积分布函数cdf,\(f(s|N)\)为负样本在预测值上的累积分布函数,则\(KS=\max_{s}{|f(s|P)-f(s|N)|}\)
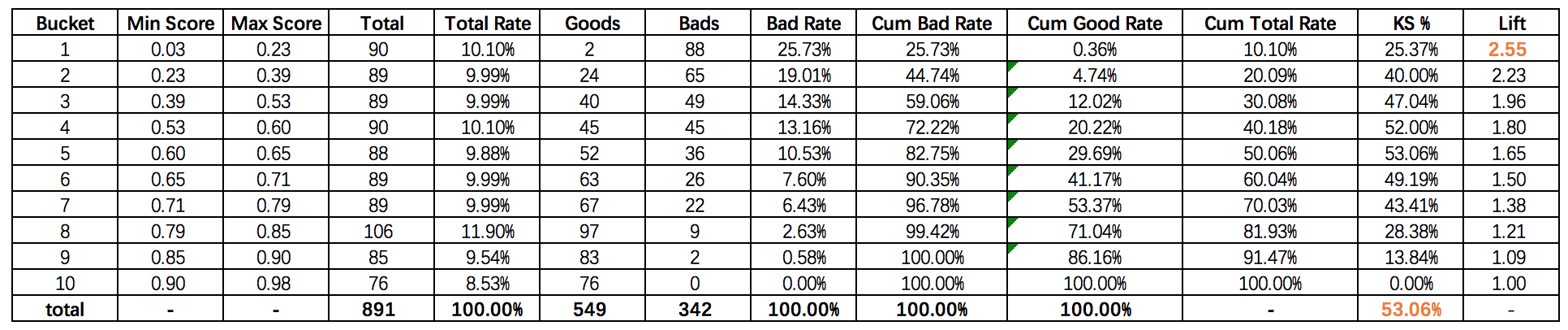
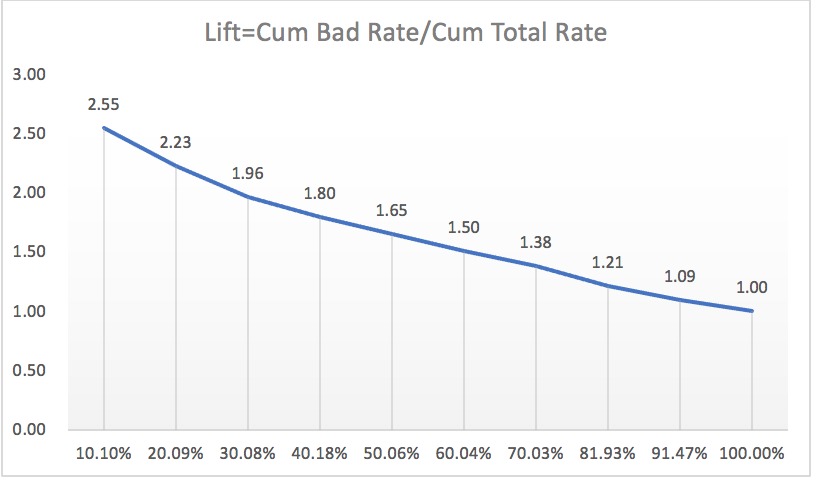
注:此表中KS=max{|累计坏人占比-累计好人占比|},Lift=Cum Bad Rate/Cum Total Rate
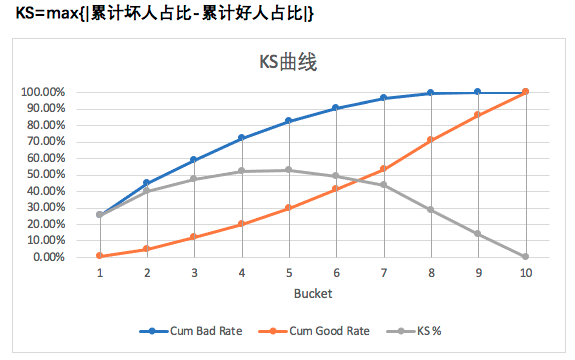
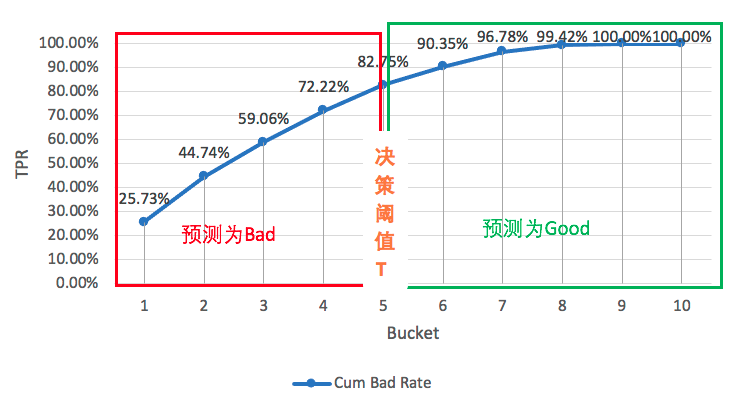
根据上图与表中的内容得到:
- 模型分数越高,逾期率越低,代表是信用评分。因此低分段的Bad Rate相对于高分段更高,Cum Bad Rate曲线增长速率比Cum Good Rate更快,Cum Bad Rate曲线在Cum Good Rate上方。
- 每个分箱里的样本数基本相同,说明是等频分箱。分箱时需要考虑样本量是否满足统计意义。
- 设策略cutoff为0.65(低于这个值的用户预测为Bad, 将会被拒绝),查表可知低于cutoff的Cum Bad Rate为82.75%,即将拒绝约82.75%的坏账户。
- 根据Bad Rate变化趋势,模型的排序性很好。若是A卡,则对排序性要求就比较高,因为需要根据风险等级对用户风险定价。
- 模型的KS达到53.06%,区分度很强,这是设定cutoff为0.65时达到的最理想的状态。实际中由于需要权衡通过率与坏账率之间的关系,一般不会设置在理想值。因此,KS统计量是好坏距离或区分度的上限。
- 通常模型的KS很少能到52%,因此需要检验模型是否发生过拟合,或数据信息泄露。
| KS% | 好坏区分能力 |
|---|---|
| <20 | 不建议采用 |
| 20~40 | 较好 |
| 41~50 | 良好 |
| 51~60 | 很强 |
| 61~75 | 非常强 |
| >75 | 能力强但疑似有误 |
ROC曲线
ROC曲线绘制步骤:
- 先按分数升序排序,计算某个阈值T下的TPR与FPR
- 重复步骤1多次,在不同阈值T下计算得到多个TPR与FPR
- 以FPR为横轴,TPR为纵轴,画出ROC曲线
注:
步骤1中,低于T时预测为Bad。
TPR=(预测为Bad & 真实为Bad)/整体真实为Bad
FPR=(预测为Bad & 真实为Good)/整体真实为Good
因此可将TPR理解为累积正样本率Cum Bad Rate,FPR理解为累积负样本率Cum Good Rate
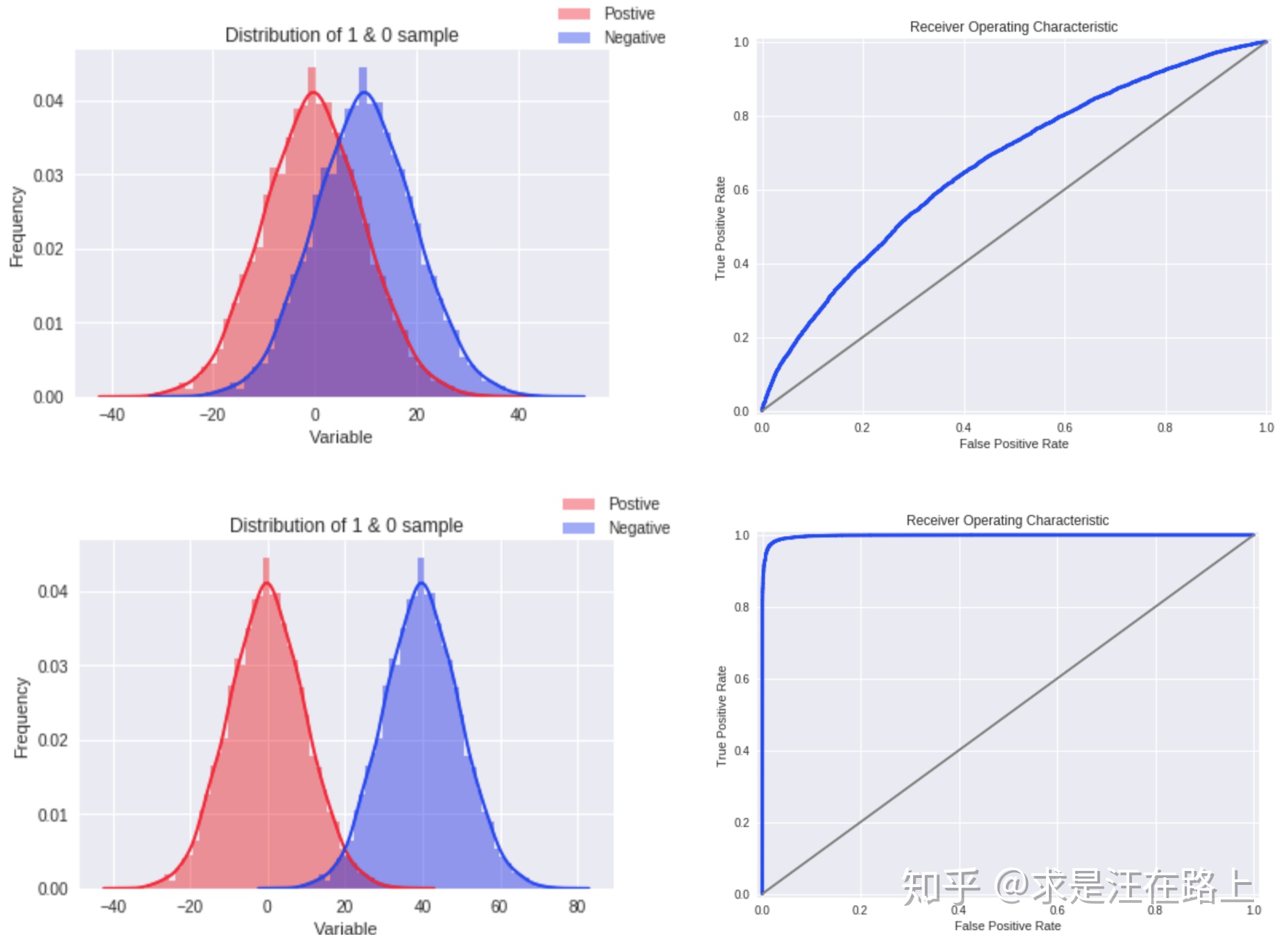
样本分布与ROC曲线之间的关系:
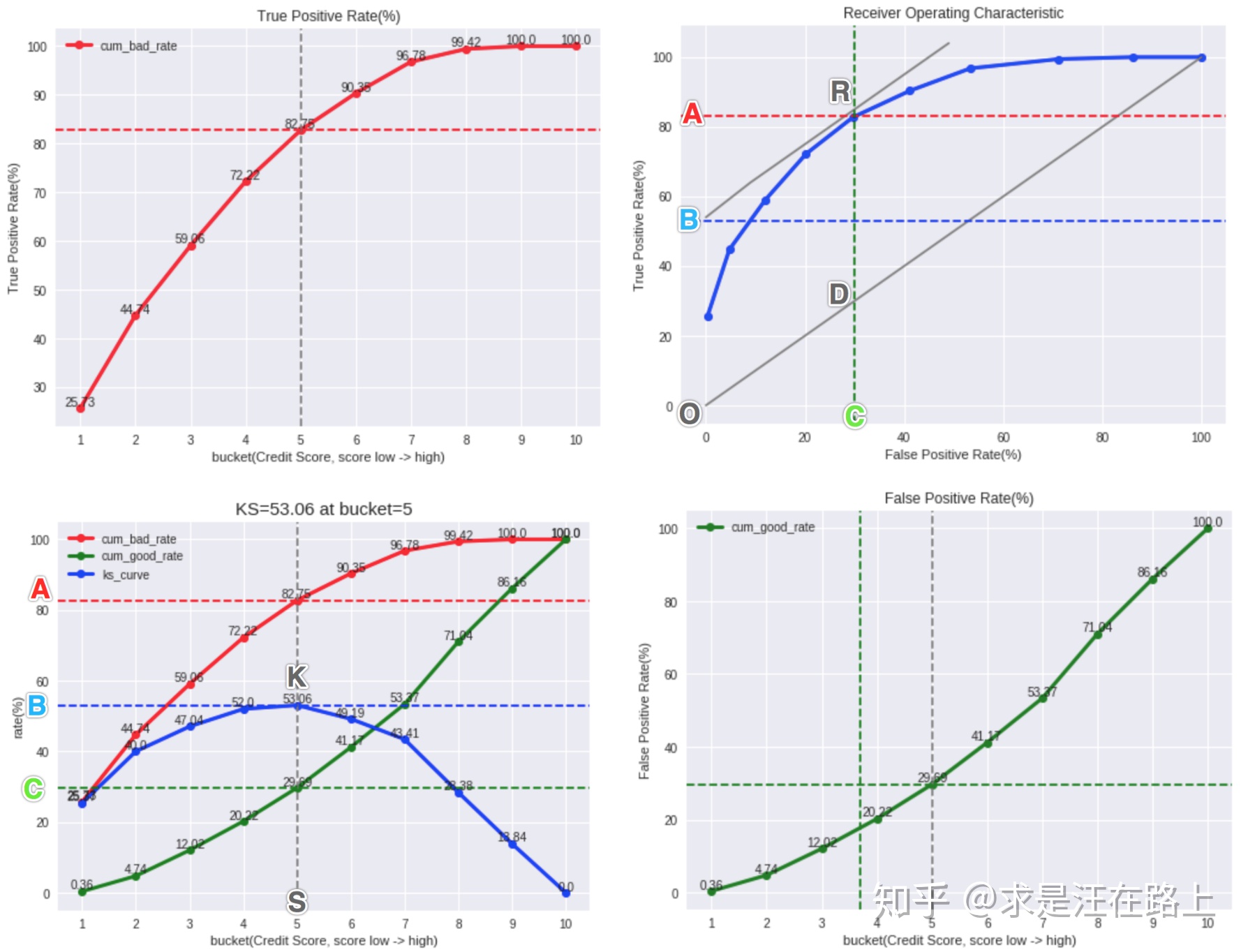
KS曲线与ROC曲线之间的关系

洛伦兹曲线与Gini系数
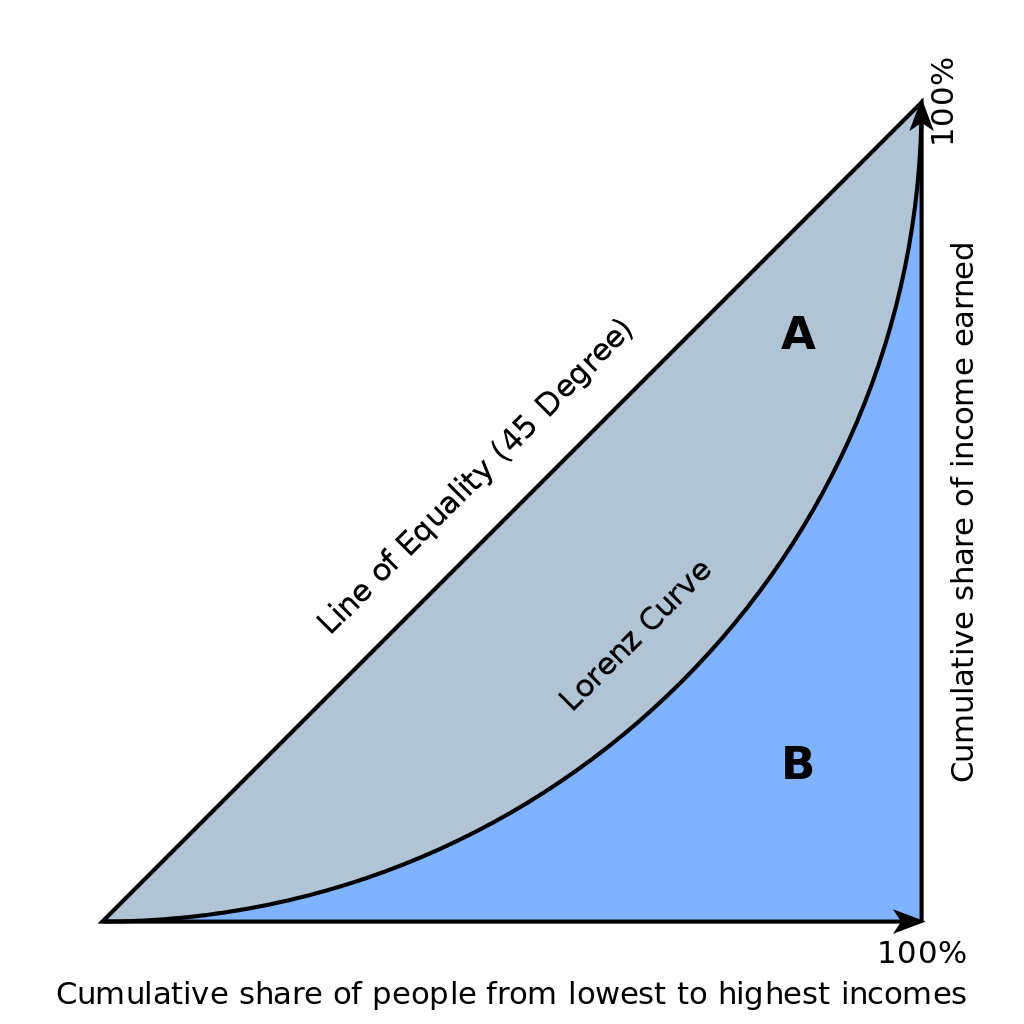
上图即为洛伦兹曲线。In economics, the Lorenz curve is a graphical representation of the distribution of income or of wealth.
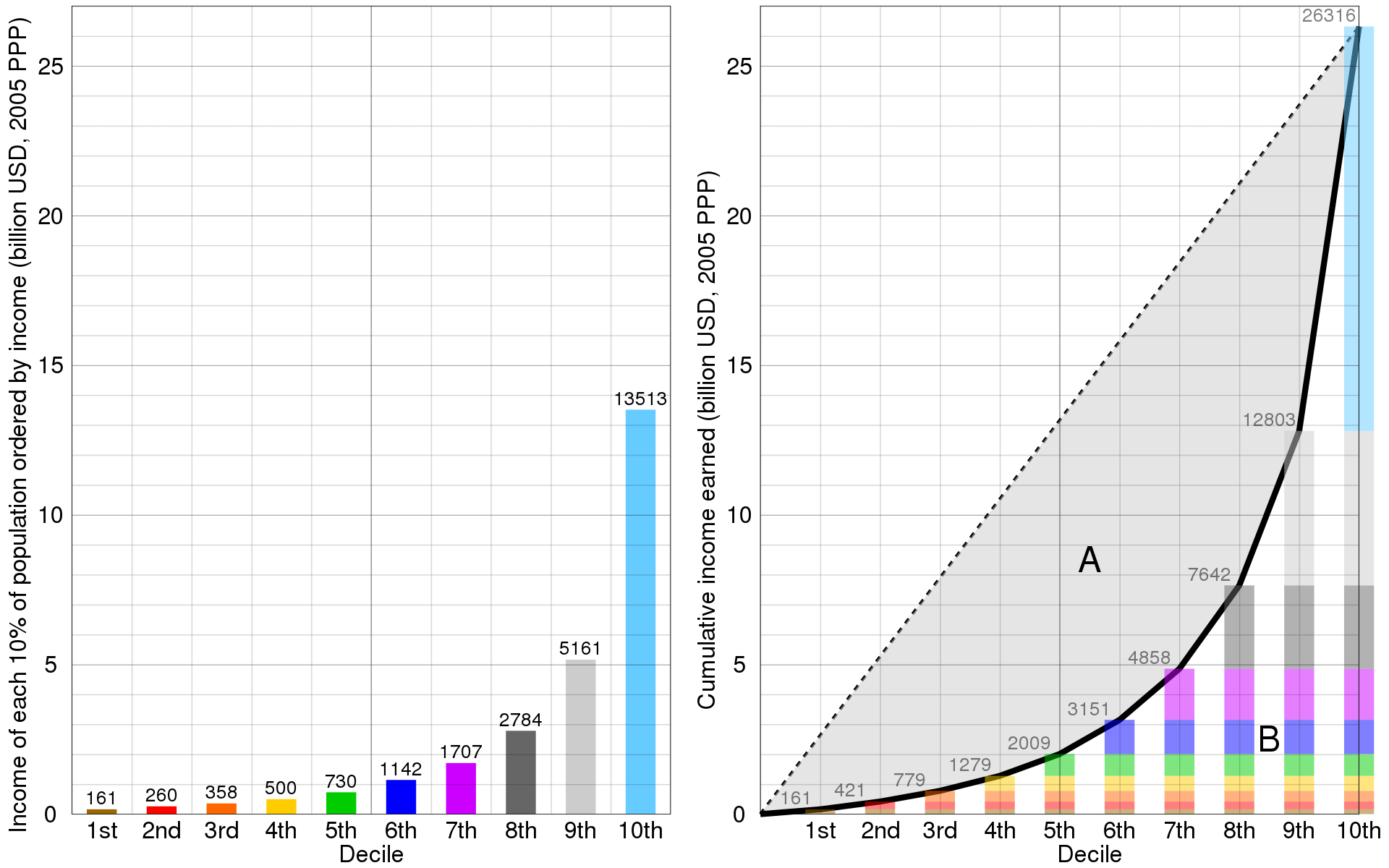
Lorenz curve上点表示含义:如“the bottom 20% of all households have 10% of the total income.”
理想状态下,每个人收入都相等,此时the bottom N% of society would always have N% of the income,图形为一条直线Y=X,称为line of perfect equality;
与之相反的是在极不平等状态下,只有一人有全部的收入,其他人都无收入。此时曲线:y=0% for all x<100%; y=100% when x=100%,称为line of perfect inequality。
Gini系数越高,分布越不平衡。\(Gini=\frac{A}{A+B}\)=2AUC-1
迁移到风控领域,纵坐标:累计坏样本占比,横坐标:累计样本占比。设基于某个累计阈值点的样本预测为坏样本,此时预测正确的样本数为TP,预测错误的样本数为FP,样本总数为TP+FP。
\(累计坏样本占比=\frac{TP}{TP+FN}=TPR\)
\(累计样本占比=\frac{TP+FP}{TP+FP+TN+FN}\)
当负样本很少时,TP和FN的值很小,可忽略不计,则\(累计样本占比=\frac{FP}{FP+TN}=FPR\)。此时,洛伦兹曲线与ROC曲线的横纵坐标取值基本一致。
Lift曲线
Lift曲线表示相较于不利用模型时,模型的提升指数。
衡量的是一个模型对目标中“响应”的预测能力优于随机选择的倍数,以1为界线,大于1的Lift表示该模型比随机选择捕捉了更多的“响应”。
\(Lift=\frac{\frac{TP}{TP+FP}}{\frac{TP+FN}{TP+FP+FN+TN}}=\frac{\frac{TP}{TP+FN}}{\frac{TP+FP}{TP+FN+FP+TN}}=\frac{预测为Bad真实为Bad/真实为Bad}{预测为Bad/全部样本}\)
分母:不使用任何模型;
分子:预测为正例的样本中的真实正例的比例。
设10000个借款人中有1000个逾期的,则这10000个借款人逾期率\(\frac{P}{P+N}=\frac{1000}{10000}=10\%\)
对这10000个借款人建模,预测出1000个逾期的(\(TP+FP=1000,TP=300\))。此时这1000人中只有300人是真实逾期的,则\(命中率=\frac{TP}{TP+FP}=30\%\)
此时,提升值\(Lift=\frac{30\%}{10\%}=3\),模型找到逾期人员的效果提升至原先(无模型)的三倍。
Lift曲线图在很高的提升值上保持一段后,迅速下降至1时,表示模型较好。
根据【KS曲线】处表格数据可绘制如下Lift曲线(还有另一种绘制方法):
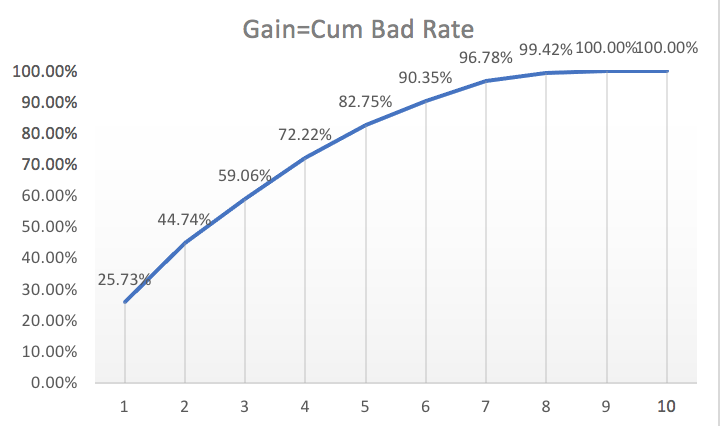
Gain曲线
\(Gain=\frac{TP}{TP+FP}\)
可参考UNDERSTAND GAIN AND LIFT CHARTS
PSI
PSI = SUM( (实际占比 - 预期占比)* ln(实际占比 / 预期占比) )
| PSI范围 | 稳定性 | 建议 |
|---|---|---|
| 0~0.1 | 好 | 没有变化或很少变化 |
| 0.1~0.25 | 略不稳定 | 有变化,继续监控后续变化 |
| >0.25 | 不稳定 | 发生大变化,进行特征项分析 |
Python代码
参考
[KS检验] https://www.cnblogs.com/arkenstone/p/5496761.html
[KS深入理解与应用] https://zhuanlan.zhihu.com/p/79934510
[风控模型评估指标介绍] https://zhuanlan.zhihu.com/p/98806525
[Lorentz Curve] https://en.wikipedia.org/wiki/Lorenz_curve
[Lift曲线与Gain曲线] https://blog.csdn.net/some_apples/article/details/104166842
[Lift曲线与Gain曲线] https://cosx.org/2009/02/measure-classification-model-performance-lift-gain
[Lift曲线] https://zhuanlan.zhihu.com/p/94323568
[UNDERSTAND GAIN AND LIFT CHARTS] https://www.listendata.com/2014/08/excel-template-gain-and-lift-charts.html
[群体稳定性指标(PSI)深入理解应用] https://zhuanlan.zhihu.com/p/79682292
https://blog.csdn.net/zwqjoy/article/details/84859405
https://blog.csdn.net/Orange_Spotty_Cat/article/details/82425113




