递归

一、算法概述
递归算法是一种直接或者间接调用自身函数或者方法的算法。说简单了就是程序自身的调用。
1
二、算法实质
递归算法就是将原问题不断分解为规模缩小的子问题，然后递归调用方法来表示
问题的解。（用同一个方法去解决规模不同的问题）
1
2
三、算法思想
递归算法，顾名思义就是有两个大的阶段：递和归，即就是有去（递去）有回（归来）。
1
递去：将递归问题分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决
归来：当你将问题不断缩小规模递去的时候，必须有一个明确的结束递去的临界点（递归出口），一旦达到这个临界点即就从该点原路返回到原点，最终问题得到解决。
递归的图解分析

 

四、递归算法的设计要素
递归思维是一种从下向上的思维方式，使用递归算法往往可以简化我们的代码，
而且还帮我们解决了很复杂的问题。递归算法的难点就在于它的逻辑性，一般设计
递归算法需要考虑以下几点:
1
2
3
明确递归的终止条件
提取重复的逻辑，缩小问题的规模不断递去
给出递归终止时的处理办法
五、递归算法的经典实例
一一问题定义即为递归定义

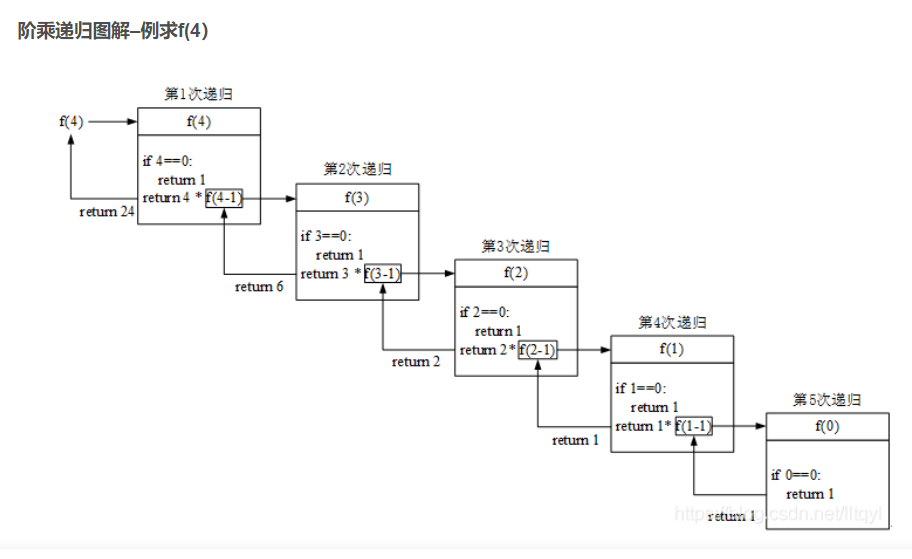
阶乘

 

 

 

f(1)=f(2)=1;                                         f(5)=f(3)+f(4)=5;

f(3)=f(1)+f(2);           　　　　　　　f(4)=f(2)+f(3)=3;

f(4)=f(2)+f(3); 　　　　　　　　　　f(3)=f(1)+f(2)=2;

f(5)=f(3)+f(4);　　　　　　　　　　f(1)=f(2)=1; 

f(n)=f(n-2)=f(n-1);

斐波纳契数列

 

 

 

杨辉三角的取值

 

 

 

 

 

 

 

 

 

 

一一问题应用递归算法来解决

hanoi塔问题
一一部分数据结构也是用递归来定义的

树
问题递归定义
●阶乘

阶乘递归图解–例求f(4）

 

●斐波纳契数列

●杨辉三角的取值

应用递归算法解决问题
●hanoi塔
在分治算法中有详细介绍。

数据结构中的递归定义
●树