LC——搜索二维矩阵 II

题目描述

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：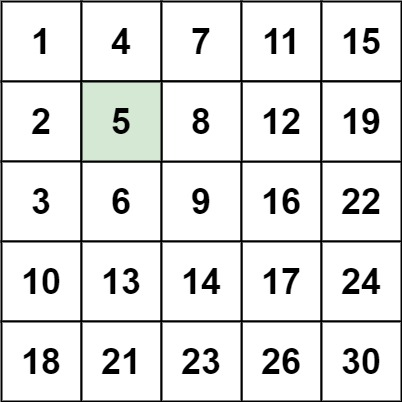

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：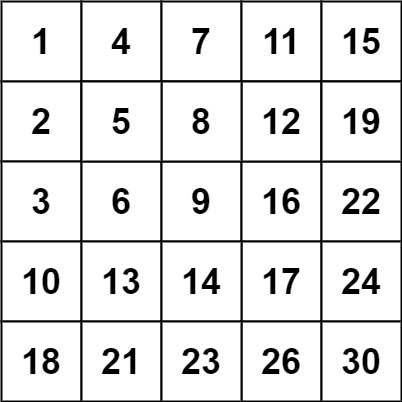

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

    m == matrix.length
    n == matrix[i].length
    1 <= n, m <= 300
    -109 <= matix[i][j] <= 109
    每行的所有元素从左到右升序排列
    每列的所有元素从上到下升序排列
    -109 <= target <= 109

方式一——二分

 1 class Solution {
 2     public boolean searchMatrix(int[][] matrix, int target) {
 3         int n = matrix.length;
 4         // 二分
 5         for (int i = 0; i < n; i++) {
 6             int index = Arrays.binarySearch(matrix[i],  target);
 7             if (index >= 0) {
 8                 return true;
 9             }
10         }
11 
12         return false;
13     }
14 }

时间复杂度：O(nlogn)

空间复杂度：O(1)

方式二——利用题目给定的排序特性找规律

选取两个点：

　　①右上角（这里我们采用右上角）

　　②左下角

 1 class Solution {
 2     public boolean searchMatrix(int[][] matrix, int target) {
 3         // 从右上角开始找（选取的地方很重要，因为选取的地方要根据指定值唯一确定下一次的走向）
 4         int row = 0;
 5         int col = matrix[0].length - 1;
 6         while (row < matrix.length && col >= 0) {
 7             int cur = matrix[row][col];
 8             if (target == cur) {
 9                 return true;
10             } else if (target < cur) {
11                 // 往左走
12                 col--;
13             } else if (target > cur) {
14                 // 往下走
15                 row++;
16             }
17         }
18 
19         return false;
20     }
21 }