2017年蓝桥杯国赛——合格植物

题目描述：

w星球的一个种植园，被分成 m * n 个小格子（东西方向m行，南北方向n列）。每个格子里种了一株合根植物。
这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。

如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？

 

输入格式

第一行，两个整数m，n，用空格分开，表示格子的行数、列数（1<m,n<1000）。
接下来一行，一个整数k，表示下面还有k行数据(0<k<100000)
接下来k行，第行两个整数a，b，表示编号为a的小格子和编号为b的小格子合根了。

格子的编号一行一行，从上到下，从左到右编号。
比如：5 * 4 的小格子，编号：
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20

 

样例输入

5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17

 

样例输出

5

 

样例说明

　　

 

 

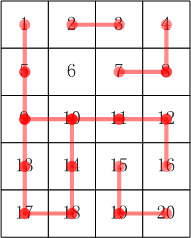
思路：并查集

那么什么是并查集呢？

并查集被很多OIer认为是最简洁而优雅的数据结构之一，主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

• 合并（Union）：把两个不相交的集合合并为一个集合。
• 查询（Find）：查询两个元素是否在同一个集合中。

当然，这样的定义未免太过学术化，看完后恐怕不太能理解它具体有什么用。所以我们先来看看并查集最直接的一个应用场景：亲戚问题。

（洛谷P1551）亲戚

题目背景
若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。
题目描述
规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。
输入格式
第一行：三个整数n,m,p，（n<=5000,m<=5000,p<=5000），分别表示有n个人，m个亲戚关系，询问p对亲戚关系。
以下m行：每行两个数Mi，Mj，1<=Mi，Mj<=N，表示Mi和Mj具有亲戚关系。
接下来p行：每行两个数Pi，Pj，询问Pi和Pj是否具有亲戚关系。
输出格式
P行，每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。

这其实是一个很有现实意义的问题。我们可以建立模型，把所有人划分到若干个不相交的集合中，每个集合里的人彼此是亲戚。为了判断两个人是否为亲戚，只需看它们是否属于同一个集合即可。因此，这里就可以考虑用并查集进行维护了。

AC代码：

import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;

public class MergePlant {

    /**
     * 查找
     * @param a 待查找的节点
     * @param parent 存储所有节点对应的根节点的数组
     * @return 返回根节点的序号，从1开始
     */
    public static int find(int a, int[] parent) {
        int root = a;
        while (parent[root] != 0) {
            root = parent[root];
        }
        return root;
    }

    /**
     * 合并
     * @param a 合并的第一个节点
     * @param b 合并的第二个节点
     * @param parent 存储根节点的数组
     * @param rank 存储树的等级，最小为0，即只有一个节点本身
     * @return 返回 true 则表示合并成功，返回 false 则表示合并失败，即两个节点是在同一棵树上
     */
    public static boolean union(int a, int b, int[] parent, int[] rank) {
        int root_a = find(a, parent);
        int root_b = find(b, parent);

        if (root_a == root_b) {
            return false;
        } else {
            if (rank[root_a] > rank[root_b]) {
                // a节点所在的树的等级 > b节点所在的树的等级
                // 将b节点所在的树合并到a节点所在的树上
                parent[root_b] = root_a;
            } else if (rank[root_a] < rank[root_b]) {
                // a节点所在的树的等级 < b节点所在的树的等级
                // 将a节点所在的树合并到b节点所在的树上
                parent[root_a] = root_b;
            } else {
                // 如果相等，只需随便选一个树合并到另外一棵树上即可，这里就让a合并到b
                // b节点所在树的等级要+1
                parent[root_a] = root_b;
                rank[root_b]++;
            }
            return true;
        }
    }

    /**
     * 将所有节点的初始根节点都设置为自身，即为0，方便后面查找根节点
     * 将所有树的等级一开始都设置为0
     * @param parent 存储根节点的数组
     */
    public static void initialization(int[] parent, int[] rank) {
        for (int i = 0; i < parent.length; i++) {
            parent[i] = 0;
            rank[i] = 0;
        }
    }

    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        int m = input.nextInt();
        int n = input.nextInt();

        // 定义根节点数组
        int[] parent = new int[m * n + 1];
        // 定义树等级数组
        int[] rank = new int[m * n + 1];

        // initialization to -1
        initialization(parent, rank);

        // 接收边的数量
        int side = input.nextInt();
        // 接收边，即节点与节点之间的关系
        // 来一个关系，合并一次
        for (int i = 0; i < side; i++) {
            int a = input.nextInt();
            int b = input.nextInt();
            union(a, b, parent, rank);
        }

        // 最后判断存储根节点的数组中还剩下几棵树，这里用Set集合来存储，为了去重
        Set<Integer> set = new HashSet<>();
        // 编号从1 ~ m * n
        for (int i = 1; i <= m * n; i++) {
            set.add(find(i, parent));
        }

        System.out.println(set.size());
    }
}

 二刷——此次将rank数组给省略了（其实是不需要的），直接在查询并将其祖先返回的时候，顺便将以该节点为根节点的所有节点的祖先更新即可。

第二次再做这个国赛中并查集的题目时，有两点没有注意：

1、合并两个根的植物时，是将一个根的植物的祖先的祖先设置为另一根植物的祖先

2、在最后统计还剩下多少个合根植物时，直接用了parent[i]导致结果出现了错误，这个错误在我第一次做时本来是没有犯的，可是随着时间也渐渐遗忘了很多细节。所以算法不是你会就能一定最后在规定时间内写出来，还要靠长时间的刷题、不断地积累经验才能做到一蹴而就。因为这一点可以说是我们之前在union()方法中遗留下来的易错点，误以为最后parent[]数组中存放的都是对应编号合根植物的祖先，其实并不然，因为当时我们在合并两株植物时只是做了这样一行代码的操作：parent[parent[a]]= parent_b；这显然没有将我们a所在这株植物上的所有节点的祖先都更新，所有要再最后统计的时候去再次调用一下find()方法，这样就可以把每柱植物对应的祖先都返回，才不会导致最终结果出错。（这也是重复刷同一题的好处，可以深刻的理解算法的精髓，每做一次都有不一样的领悟，都有可能会犯前面几次不会犯的错误）

import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;

public class 合根植物 {
    
    private static int[] parent;
    
    /**
     * 查询
     */
    public static int find(int x) {
    　　if (parent[x] != x) {
        　　parent[x] = find(parent[x]);
    　　}
    
    　　return parent[x];
    }
    
    /**
     * 合并
     */
    public static void union(int a, int b, int n) {
    　　int parent_a = find(a);
    　　int parent_b = find(b);
    　　if (parent_a == parent_b) {
        　　return;
    　　}
    
   　　 // 注意点：两个树合并，是将两个树中的其中一棵树的根节点作为另一棵树的根节点的新根节点，所以是祖先的祖先
    　　// 将a的祖先的祖先设置为b的祖先
    　　parent[parent[a]]= parent_b;
    }
    
    /**
     * 初始化，每个元素一开始都是以自身作为祖先
     */
    public static void initialization(int n) {
    　　for (int i = 1; i <= n; i++) {
        　　parent[i] = i;
    　　}
    }
    
    public static void main(String[] args) {
    　　Scanner input = new Scanner(System.in);
    　　int m = input.nextInt();
    　　int n = input.nextInt();
    　　parent = new int[m * n + 10];
    　　initialization(m * n);
    　　int k = input.nextInt();
    　　// 下面就是可能发现合根的植物的编号对
    　　for (int i = 0; i < k; i++) {
       　　 int a = input.nextInt();
        　　int b = input.nextInt();
       　　 union(a, b, m * n);
   　　 }
    　　input.close();
    
    　　Set<Integer> set = new HashSet<>();
    　　for (int i = 1; i <= m * n; i++) {
       　　 // 这里容易忽视，其实是在加入集合之前去找一下该植物的祖先，因为之前只是祖先与祖先相连，而并没有修改子代
       　　 set.add(find(i));
   　　 }
    　　System.out.println(set.size());
    }
}