最大子段和——蛮力、分治和动态规划
什么是最大字段和?
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n 例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-20,11,-4,13,-5,-2)时,最大子段和为20。
最大子段和是动态规划中的一种。
问题描述
- 求一个序列的最大子段和即最大连续子序列之和。例如序列[4, -3, 5, -2, -1, 2, 6, -2]的最大子段和为11=[4+(-3)+5+(-2)+(-1)+(2)+(6)]。
一、蛮力法——时间复杂度为O(n^3)
C++代码:
1 #include<iostream> 2 using namespace std; 3 int MaxSubsequenceSum(const int array[], int n) 4 { 5 int tempSum, maxSum; 6 maxSum = 0; 7 for (int i = 0;i < n;i++) // 子序列起始位置 8 { 9 for (int j = i;j < n;j++) // 子序列终止位置 10 { 11 tempSum = 0; 12 for (int k = i;k < j;k++) // 子序列遍历求和 13 tempSum += array[k]; 14 if (tempSum > maxSum) // 更新最大和值 15 maxSum = tempSum; 16 } 17 } 18 return maxSum; 19 } 20 21 int main() 22 { 23 const int a[] = { 4, -3, 5, -2, -1, 2, 6, -2 }; 24 int maxSubSum = MaxSubsequenceSum(a, 8); 25 cout << "The max subsequence sum of a is: " << maxSubSum << endl; 26 system("pause"); 27 return 0; 28 }
二、分治法
算法描述如下
针对最大子段和这个具体问题本身的结构,我们还可以从算法设计的策略上对上述O(n^2)计算时间算法进行更进一步的改进。从问题的解结构也可以看出,它适合于用分治法求解。
如果将所给的序列a[1:n]分为长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大子段和,则a[1:n]的最大子段和有三种情况:
(1) a[1:n]的最大子段和与a[1:n/2]的最大子段和相同
(2) a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同
(3) a[1:n]的最大子段和为a[i]+…+a[j],并且1<=i<=n/2,n/2+1<=j<=n。
对于(1)和(2)两种情况可递归求得,但是对于情况(3),容易看出a[n/2],a[n/2+1]在最大子段中。因此,我们可以在a[1:n/2]中计算出s1=max(a[n/2]+a[n/2-1]+…+a[i]),0<=i<=n/2,并在a[n/2+1:n]中计算出s2= max(a[n/2+1]+a[n/2+2]+…+a[i]),n/2+1<=i<=n。则s1+s2为出现情况(3)的最大子段和。据此可以设计出最大子段和问题的分治算法如下:(C++代码)
1 #include<stdio.h> 2 #define MAX 100 3 int maxsub(int left,int right); 4 int a[MAX]; 5 int main() 6 { 7 int i,count; 8 scanf("%d",&count); 9 for(i=0;i<count;i++) 10 scanf("%d",&a[i]); 11 printf("%d\n",maxsub(0,count-1)); 12 return 0; 13 } 14 int maxsub(int left,int right) 15 { 16 int center,i,sum,left_sum,right_sum,left_max,right_max; 17 center=(left+right)>>1; 18 if(left==right) 19 return a[left]>0?a[left]:0; 20 else 21 { 22 left_sum=maxsub(left,center); 23 right_sum=maxsub(center+1,right); 24 sum=0; 25 left_max=0; 26 for(i=center;i>=left;i--) 27 { 28 sum+=a[i]; 29 if(sum>left_max) 30 left_max=sum; 31 } 32 sum=0; 33 right_max=0; 34 for(i=center+1;i<=right;i++) 35 { 36 sum+=a[i]; 37 if(sum>right_max) 38 right_max=sum; 39 } 40 sum=right_max+left_max; 41 if(sum<left_sum) 42 sum=left_sum; 43 if(sum<right_sum) 44 sum=right_sum; 45 } 46 return sum; 47 }
算法复杂度
分析:假设求解N个元素序列的最大子问题的时间复杂度为T(N),则T(N)
满足:
T(N)=2T(N/2)+O(N)
且T(1)=1,其中,T(N/2)表式分治后的左右两边求解复杂度,O(N)为求解跨越左右边界的最大子段和的开销。求解该递推公式得递归算法复杂度为T(N)=O(NlogN)
-
递归算法的基本准则:
- (1) 基准情形:存在最小子问题的解,也称为递归终止的条件。
- (2) 不断推进:每一次递归调用都要使得求解状况不断地朝基准情形方向推进。
- (3) 设计法则:假设所有递归调用都能运行。
- (4) 合成效益法则:在求解一个问题的同一实例式,要避免在不同的递归调用中做重复的工作。如:递归求斐波那契数就是一个不好的例子。
三、动态规划——算法时间复杂度为O(n)
- 原问题:考虑最大子段和原问题:给定n个数(可以为负数)的序列(a1,a2,...,an),求max{0,max1≤i≤j≤n∑jk=iak}
- 子问题界定:设前边界为1,后边界为i,且C(i)是子序列A[1,..i]必须包含元素A[i]的向前连续延伸的最大子段和:
C[i]=max1≤k≤i{∑j=kiA[j]}

- 递推方程满足:
C[i]=max{C[i−1]+A[i], A[i]}i=2,...,n
{ A[1] ifA[1]>0
C[1] =
{ 0 ifA[1]<0
- 遍历所有以i (1≤i≤n)为后边界的最大子段和Ci得出最优解:
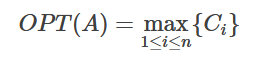
OP
OP
动态规划算法设计要点:
(1) (划分)多阶段决策过程,每步处理一个子问题,界定子问题的边界(初值问题)。
(2) 列出优化函数的递推方程及初值(无比关键)。
(3) 问题要满足优化原则或者最优子结构性质。即:一个最优决策序列的任何子序列本身一定是相对于子序列的初始和结束状态的最优决策序列。
Java代码如下:
1 class Solution { 2 public int maxSubArray(int[] arr) { 3 int max = Integer.MIN_VALUE; 4 int total = 0; 5 for (int i = 0; i < arr.length; i++) { 6 if (total > 0) { 7 total += arr[i]; 8 } else { 9 total = arr[i]; 10 } 11 if (total > max) { 12 max = total; 13 } 14 } 15 return max; 16 } 17 }
分类:
算法分析与设计










【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· DeepSeek在M芯片Mac上本地化部署
· 葡萄城 AI 搜索升级:DeepSeek 加持,客户体验更智能