动态规划算法

数学归纳法引出动态规划算法的思想

 

我们解决动态规划问题一般分为四步：

1、确定状态

2、转移方程

3、初始条件和边界情况

4、计算顺序

 

经典例题：

1、斐波拉契数列（自顶向下）递归版本

这个代码的时间复杂度是2^n，也就是指数递增，我们经过测试当求一个很大数字的时候，这个时间可想而知很长

public static int Fibonacci(int n) {
        if(n<=0)
            return 0;
        if(n == 1 || n == 2)
            return 1;
        return Fibonacci(n-1)+Fibonacci(n-2);
    }
}

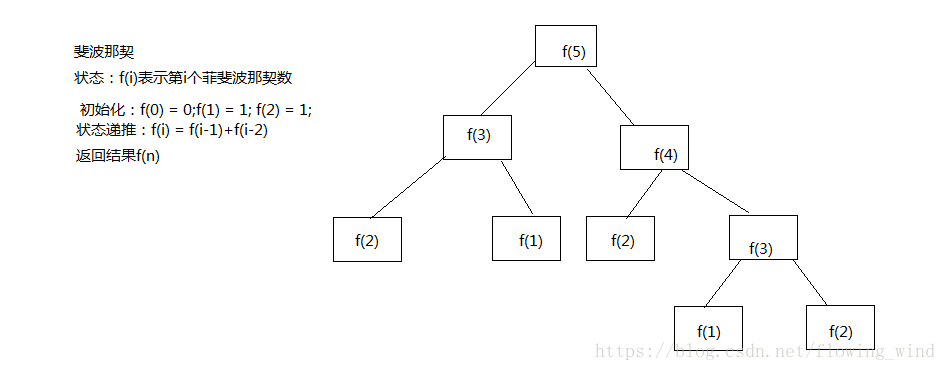
动态规划版

public static int topDownFibonacci(int n, int[] arr) {
        // 初始化arr数组的所有值为-1，表示该斐波那契数列还没有被计算
        for (int i = 0; i < arr.length; i++) {
            arr[i] = -1;
        }
        
        // 求第n个数是多少
        return fibonacci(n, arr);
    }
    
    public static int fibonacci(int n, int[] arr) {
        if (arr[n] != -1) {
            return arr[n];
        }
        
        int result = fibonacci(n - 1, arr) + fibonacci(n - 2, arr);
        // 标记第n个数已经计算好了，下次可以直接拿
        arr[n] = result;
        // 返回给调用者，因为这是上一级调用者要求的数，现在求好了可以往上返回。
        return arr[n];
    }

迭代版

/**
     * 迭代版
     * @param n
     * @return
     */
    public static int fibonacci(int n) {
        if (n <= 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        int f1 = 0;
        int f2 = 1;
        int result = 0;
        for (int i = 2; i <= n; i++) {
            // 递推公式
            result = f1 + f2;
            // 将原来的f2赋值给f1
            f1 = f2;
            // 将结果赋值给f2
            f2 = result;
        }

        return result;
    }