2015年第六届蓝桥杯省赛JavaB组——第九题垒骰子
题目：垒骰子
赌圣atm晚年迷恋上了垒骰子，就是把骰子一个垒在另一个上边，不能歪歪扭扭，要垒成方柱体。
经过长期观察，atm 发现了稳定骰子的奥秘：有些数字的面贴着会互相排斥！
我们先来规范一下骰子：1 的对面是 4，2 的对面是 5，3 的对面是 6。
假设有 m 组互斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。 atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多，请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦～
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行，每行两个整数 a b ，表示 a 和 b 不能紧贴在一起。
「输出格式」
一行一个数，表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
「数据范围」
对于 30% 的数据：n <= 5
对于 60% 的数据：n <= 100
对于 100% 的数据：0 < n <= 10^9, m <= 36
资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 2000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意：不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意：主类的名字必须是：Main，否则按无效代码处理。
一开始自己的做法：采用递归求解
package com.lzp.lanqiaosix.p9; import java.util.ArrayList; import java.util.List; import java.util.Scanner; /** * @Author LZP * @Date 2021/3/8 20:03 * @Version 1.0 * <p> * 垒骰子 * <p> * 赌圣atm晚年迷恋上了垒骰子，就是把骰子一个垒在另一个上边，不能歪歪扭扭，要垒成方柱体。 * 经过长期观察，atm 发现了稳定骰子的奥秘：有些数字的面贴着会互相排斥！ * 我们先来规范一下骰子：1 的对面是 4，2 的对面是 5，3 的对面是 6。 * 假设有 m 组互斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。 atm想计算一下有多少种不同的可能的垒骰子方式。 * 两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同 。 * 由于方案数可能过多，请输出模 10^9 + 7 的结果。 * <p> * 不要小看了 atm 的骰子数量哦～ * <p> * 「输入格式」 * 第一行两个整数 n m * n表示骰子数目 * 接下来 m 行，每行两个整数 a b ，表示 a 和 b 不能紧贴在一起。 * <p> * 「输出格式」 * 一行一个数，表示答案模 10^9 + 7 的结果。 * <p> * 「样例输入」 * 2 1 * 1 2 * <p> * 「样例输出」 * 544 * <p> * 「数据范围」 * 对于 30% 的数据：n <= 5 * 对于 60% 的数据：n <= 100 * 对于 100% 的数据：0 < n <= 10^9, m <= 36 * <p> * <p> * 资源约定： * 峰值内存消耗（含虚拟机） < 256M * CPU消耗 < 2000ms * <p> * <p> * 请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。 * <p> * 所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。 * 注意：不要使用package语句。不要使用jdk1.7及以上版本的特性。 * 注意：主类的名字必须是：Main，否则按无效代码处理。 * <p> * <p> * 本次决策先考虑满足60% 的数据 n <= 100 * * 方案一： * 递归求解，只要骰子数一多，时间复杂度就会指数增长，爆炸 */ public class Main { private static int[][] arr; private static int[][] temp; private static List<int[][]> dp = new ArrayList<>(100); private static int count; /** * 骰子数量 */ private static int n; /** * 互斥的组数 */ private static int m; private static int mod = 1000000000 + 7; public static void main(String[] args) { Scanner input = new Scanner(System.in); n = input.nextInt(); m = input.nextInt(); arr = new int[m][2]; temp = new int[n][10]; for (int i = 0; i < m; i++) { arr[i][0] = input.nextInt(); arr[i][1] = input.nextInt(); } // 刚一开始，先讨论怎么垒第一个骰子，一开始为啥填0，因为要是0，第一个骰子想怎么垒就怎么垒，不用担心互相排斥的问题 f(0, 1); System.out.println(count); } /** * @param topAspect * @param k */ public static void f(int topAspect, int k) { // 出口 if (k == n + 1) { // 两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同 。 // 校验当前垒的方式是否有和集合中的所有方式中的某一种相同 if (!isSame()) { int[][] t = new int[n][10]; for (int i = 0; i < t.length; i++) { t[i][0] = temp[i][0]; t[i][1] = temp[i][1]; t[i][2] = temp[i][2]; t[i][3] = temp[i][3]; t[i][4] = temp[i][4]; t[i][5] = temp[i][5]; } dp.add(t); count++; count %= mod; } return; } // 当前垒的是第k个骰子，在垒第k个筛子前，都要校验当前要放上去的这个骰子是否跟此时最顶上（也就是第k - 1）的骰子有互相排斥的情况 // 骰子有六个面，所以每个骰子都有6次选择，到底选哪个面垒在最底下 // i代表此时垒在最顶上的骰子的底面数字 for (int i = 1; i <= 6; i++) { int bottom = i; int top = reverseAspect(i); // 确定了底面之后，周围的四个面还可以分4个情况 for (int front = 1; front <= 6; front++) { if (front == bottom || front == top) { continue; } int fr = front; int re = reverseAspect(front); int right = getRight(bottom, fr); int left = reverseAspect(right); if (check(topAspect, bottom, k)) { // 定义骰子 /* 规则：前 0 后 1 左 2 右 3 上 4 下 5 */ // 给当前骰子的各个位置赋值 temp[k - 1][0] = fr; temp[k - 1][1] = re; temp[k - 1][2] = left; temp[k - 1][3] = right; temp[k - 1][4] = top; temp[k - 1][5] = bottom; f(top, k + 1); } } } } public static int getRight(int bottom, int front) { if (front == 1) { if (bottom == 2) { return 6; } else if (bottom == 3) { return 2; } else if (bottom == 5) { return 3; } else if (bottom == 6) { return 5; } } else if (front == 2) { if (bottom == 1) { return 3; } else if (bottom == 3) { return 4; } else if (bottom == 4) { return 6; } else if (bottom == 6) { return 1; } } else if (front == 3) { if (bottom == 1) { return 5; } else if (bottom == 2) { return 1; } else if (bottom == 4) { return 2; } else if (bottom == 5) { return 4; } } else if (front == 4) { if (bottom == 2) { return 3; } else if (bottom == 3) { return 5; } else if (bottom == 5) { return 6; } else if (bottom == 6) { return 2; } } else if (front == 5) { if (bottom == 1) { return 6; } else if (bottom == 3) { return 1; } else if (bottom == 4) { return 3; } else if (bottom == 6) { return 4; } } else if (front == 6) { if (bottom == 1) { return 2; } else if (bottom == 2) { return 4; } else if (bottom == 4) { return 5; } else if (bottom == 5) { return 1; } } return -1; } public static boolean isSame() { if (dp.size() == 0) { return false; } for (int i = 0; i < dp.size(); i++) { int[][] temArr = dp.get(i); for (int j = 0; j < temArr.length; j++) { if (temArr[j][0] != temp[j][0] || temArr[j][1] != temp[j][1] || temArr[j][2] != temp[j][2] || temArr[j][3] != temp[j][3] || temArr[j][4] != temp[j][4] || temArr[j][5] != temp[j][5]) { return false; } } } return true; } /** * 找指定数的对立面数字 * * @param n 指定数n * @return 返回对立面数子 */ public static int reverseAspect(int n) { switch (n) { case 1: return 4; case 2: return 5; case 3: return 6; case 4: return 1; case 5: return 2; case 6: return 3; default: return -1; } } /** * 校验当前第k个骰子是否跟此时最顶上的骰子有互相排斥的情况 * * @param topAspect 顶面是什么数字 * @param bottomAspect 底面是什么数字 * @param k 第k个骰子 * @return */ public static boolean check(int topAspect, int bottomAspect, int k) { for (int i = 0; i < arr.length; i++) { int a = arr[i][0]; int b = arr[i][1]; if ((topAspect == a && bottomAspect == b) || (topAspect == b && bottomAspect == a)) { // 相互排斥 return false; } } return true; } }
4个骰子可以出来
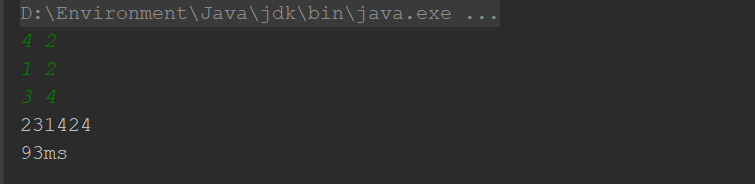
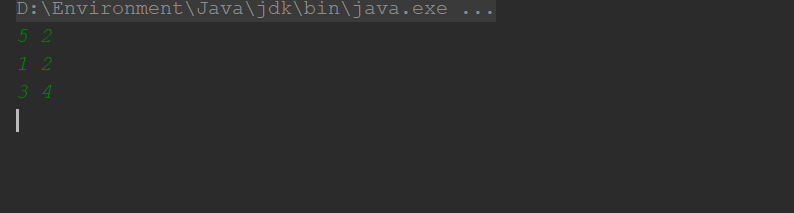
5个骰子开始就超时了，别说超时了，稍微大点的数据量直接报OOM，显然递归不适合求解这类DP（DP：多决策问题最优化选择）问题 运行结果：
方式一：动态规划与滚动数组相结合
package com.lzp.lanqiaosix.p9; import java.util.Scanner; /** * @Author LZP * @Date 2021/3/9 21:54 * @Version 1.0 * * 垒骰子 * <p> * 赌圣atm晚年迷恋上了垒骰子，就是把骰子一个垒在另一个上边，不能歪歪扭扭，要垒成方柱体。 * 经过长期观察，atm 发现了稳定骰子的奥秘：有些数字的面贴着会互相排斥！ * 我们先来规范一下骰子：1 的对面是 4，2 的对面是 5，3 的对面是 6。 * 假设有 m 组互斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。 atm想计算一下有多少种不同的可能的垒骰子方式。 * 两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同 。 * 由于方案数可能过多，请输出模 10^9 + 7 的结果。 * <p> * 不要小看了 atm 的骰子数量哦～ * <p> * 「输入格式」 * 第一行两个整数 n m * n表示骰子数目 * 接下来 m 行，每行两个整数 a b ，表示 a 和 b 不能紧贴在一起。 * <p> * 「输出格式」 * 一行一个数，表示答案模 10^9 + 7 的结果。 * <p> * 「样例输入」 * 2 1 * 1 2 * <p> * 「样例输出」 * 544 * <p> * 「数据范围」 * 对于 30% 的数据：n <= 5 * 对于 60% 的数据：n <= 100 * 对于 100% 的数据：0 < n <= 10^9, m <= 36 * <p> * <p> * 资源约定： * 峰值内存消耗（含虚拟机） < 256M * CPU消耗 < 2000ms * <p> * <p> * 请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。 * <p> * 所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。 * 注意：不要使用package语句。不要使用jdk1.7及以上版本的特性。 * 注意：主类的名字必须是：Main，否则按无效代码处理。 * * 方案二： * 动态规划，采用滚动数组 * 什么是滚动数组？ * 以前总在一些网上的算法题上看到网友提到滚动数组，但是具体怎么实现一直没搞明白，今天借这道题又去网上查阅了一下，看到一篇网友 * 的博客，内容就是这道题的解题思路、方法和C++源码，里面的方式一采用的是动态规划的算法思想， 而又因为这道题的最大骰子数给的是 * 10^9，对于这个数字，如果要一个一个迭代的去解决的话，那么是会超时的，也就是在规定的时间内肯定跑不成功，而且也开辟不出来这么 * 大的数组，所以这种算法对于这道题来讲，要想满足100%的数据正确且高效，还是有局限的。（不过也是可以学习一下的） */ public class DynamicDP { /** * 滚动数组 (0 .. 1滚动) * dp[i][j] 代表第i个骰子数字j在顶上面时垒的方式有几种 * 这里要注意，不能用int类型数组，要用long类型，不然很容易会越界 */ private static long[][] dp = new long[2][7]; /** * 对立面数组，reverseAspect[i] = j代表数字i的对立面是数字j */ private static int[] reverseAspect = new int[7]; /** * conflict[i][j] = true 代表数字i与数字j冲突 */ private static boolean[][] conflict = new boolean[7][7]; /** * 骰子数量 */ private static int n; /** * 冲突的组数 */ private static int m; /** * 滚动的标志 */ private static int e = 0; private static int mod = 1000000000 + 7; // 1e9 public static void main(String[] args) { Scanner input = new Scanner(System.in); n = input.nextInt(); m = input.nextInt(); // 初始化冲突数组 for (int i = 0; i < m; i++) { int a = input.nextInt(); int b = input.nextInt(); // 这里一定要注意：用数组来判别两个数是否互相冲突，顺序反了也是，只要仍然是这两个数那就是互相冲突的 conflict[a][b] = true; conflict[b][a] = true; } // 初始化对立面数组 reverseAspect[1] = 4; reverseAspect[2] = 5; reverseAspect[3] = 6; reverseAspect[4] = 1; reverseAspect[5] = 2; reverseAspect[6] = 3; // 表示每选一个数在顶上时都有四种方式，因为骰子周围有四个面 long C = 4; // 先直接考虑垒第一个骰子，不需要考虑其他，因为第一个骰子没有上一个骰子 for (int i = 1; i < 7; i++) { // 这里，第一个骰子每个面在上面都是一个垒的方式 dp[e][i] = 1; } // 再考虑第2到第n个骰子垒的方式 // 下面的三个循环中的变量i、j、k分别代表第i个骰子、第i个骰子顶上的数字j、第i - 1个骰子顶上的数字k for (int i = 2; i <= n; i++) { // 改变滚动标志 e = 1 - e; C = C * 4 % mod; // 选哪个面在顶上面，每个面在上面，都有四种方式，所以后面要乘以 for (int j = 1; j < 7; j++) { // 重置第i个骰子数字j在顶上面是的方式等于0 dp[e][j] = 0; for (int k = 1; k < 7; k++) { // 判断当前第i个骰子的底面数字和第i - 1个骰子的顶面数字k是否互相冲突 if (!conflict[reverseAspect[j]][k]) { // 不冲突 dp[e][j] += dp[1- e][k]; dp[e][j] %= mod; } } dp[e][j] %= mod; } } long sum = 0; for (int i = 1; i < 7; i++) { sum = (sum + (dp[e][i] * C)) % mod; } System.out.println(sum); } }
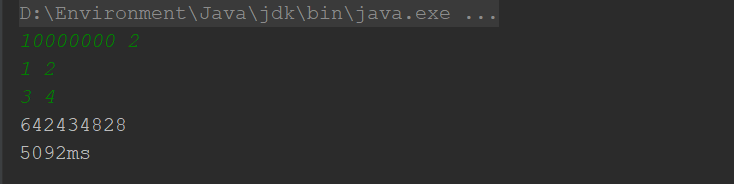
运行结果：
方式二：矩阵快速幂（以下图片是参考别人博客的，链接：https://my.oschina.net/u/4269310/blog/3668348）
package com.lzp.lanqiaosix.p9; import java.util.Arrays; import java.util.Scanner; /** * @Author LZP * @Date 2021/3/10 17:20 * @Version 1.0 * * 方案三：矩阵快速幂 */ public class MatrixQPow { /** * 这里的A就是代表一个骰子 */ private static Matrix dice; /** * 这里的conflict代表冲突矩阵 * conflict.arr[i][j] = 0 代表第k个骰子i朝上，第k - 1个骰子j朝上时会发生冲突（也就是表示某一个骰子跟它下面的一个骰子垒的关系） */ private static Matrix conflict; private static int mod = 1000000000 + 7; /** * 对立面 */ private static int[] reverseAspect = {0, 4, 5, 6, 1, 2, 3}; /** * 初始化冲突数组 */ public static void initConflict() { for (int i = 0; i < conflict.arr.length; i++) { // 这里将冲突数组先全部初始化为4，因为一个骰子面朝上的情况有4种，要么现在直接乘以4，要么最后来乘 Arrays.fill(conflict.arr[i], 4); } } /** * 矩阵连乘 * @param a * @param b * @return */ public static Matrix matrix_multi(Matrix a, Matrix b) { Matrix temp = new Matrix(a.n, b.m); for (int i = 0; i < temp.n; i++) { for (int j = 0; j < temp.m; j++) { long c = 0; for (int row = 0; row < b.n; row++) { long p1 = a.arr[i][row]; long p2 = b.arr[row][j]; c += (p1 * p2 % mod); c %= mod; } temp.arr[i][j] = c; temp.arr[i][j] %= mod; } } return temp; } /** * 矩阵快速幂 * @param A 矩阵 * @param n 幂个数 * @return */ public static Matrix matrix_qPow(Matrix A, long n) { // 返回单位矩阵 Matrix unit = getUnitMatrix(A); while (n != 0) { if (n % 2 == 1) { unit = matrix_multi(unit, A); } // 缩指数 A = matrix_multi(A, A); n = n >> 1; } return unit; } /** * 返回单位矩阵 * @param matrix * @return */ public static Matrix getUnitMatrix(Matrix matrix) { Matrix unit = new Matrix(matrix.n, matrix.m); for (int i = 0; i < unit.n; i++) { for (int j = 0; j < unit.m; j++) { if (i == j) { // 单位矩阵：主对角线全为1，其他全为0 unit.arr[i][j] = 1; } } } return unit; } public static void main(String[] args) { Scanner input = new Scanner(System.in); int n = input.nextInt(); int m = input.nextInt(); // 创建第一个骰子 dice = new Matrix(6, 6); for (int i = 0; i < dice.n; i++) { // 初始化为4 dice.arr[i][0] = 4; } // 初始化冲突矩阵，并指定冲突 conflict = new Matrix(6, 6); initConflict(); for (int i = 0; i < m; i++) { int p1 = input.nextInt(); int p2 = input.nextInt(); // conflict.arr[i][j] 表示的是，顶面i和顶面j互相冲突.这里i和j代表的都是顶面，所以要求其中一个要转换为自己的对立面 conflict.arr[p1 - 1][reverseAspect[p2] - 1] = 0; conflict.arr[p2 - 1][reverseAspect[p1] - 1] = 0; } // 先求矩阵A^n - 1次幂， Matrix A = matrix_qPow(conflict, n - 1); // 再求A^n - 1与第一个骰子的矩阵幂 A = matrix_multi(A, dice); long sum = 0; for (int i = 0; i < 6; i++) { sum = sum + A.arr[i][0]; sum %= mod; } System.out.println(sum); } } /* 矩阵类 */ class Matrix { // 矩阵的行 int n; // 矩阵的列 int m; // 矩阵本身，这里用二维数组实现 long[][] arr = new long[6][6]; public Matrix(int n, int m) { this.n = n; this.m = m; } }
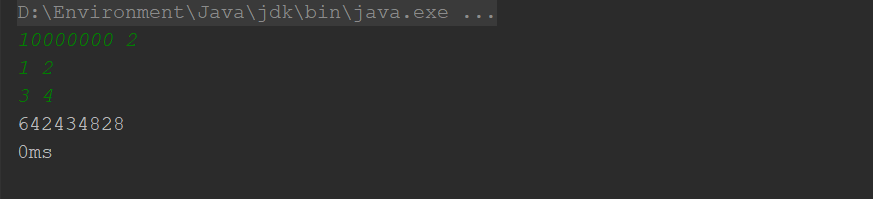
运行结果：
观察以上两种方式，我们可以发现，如果简单的用动态规划去一步步迭代出结果，那代码跑出来肯定是超时的，但是如果把矩阵乘法和快速幂两者相结合——实现矩阵快速幂，也就是通过整数的快速幂递推到矩阵的快速幂，这样的话我们可以把原来的O(n)时间复杂度降低到O(log(n))，从而大大提高了程序的运行效率。
