二叉树的深度优先遍历和广度优先遍历
深度优先搜索:深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点(即那些不包含任何超链的HTML文件) 。在一个HTML文件中,当一个超链被选择后,被链接的HTML文件将执行深度优先搜索,即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止,然后返回到某一个HTML文件,再继续选择该HTML文件中的其他超链。当不再有其他超链可选择时,说明搜索已经结束。
宽度优先搜索:宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
两者分别结合栈、队列实现
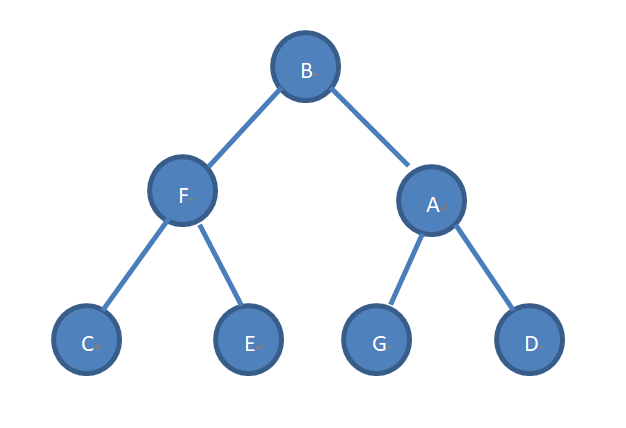
一、生成二叉树
二、编写一个Node类
package com.lzp.util.tree;
/**
* @Author LZP
* @Date 2021/2/22 12:53
* @Version 1.0
*/
public class Node {
/**
* 左孩子
*/
public Node left;
/**
* 右孩子
*/
public Node right;
/**
* 当前节点的值
*/
public char data;
public Node(Node left, Node right, char data) {
this.left = left;
this.right = right;
this.data = data;
}
}
三、编写一个BTreeUtil工具类
package com.lzp.util.tree;
import java.util.Queue;
import java.util.Stack;
import java.util.concurrent.ArrayBlockingQueue;
/**
* @Author LZP
* @Date 2021/2/22 8:34
* @Version 1.0
*
* 二叉树
*/
public class BTreeUtil {
/**
* 创建二叉树
* @param arr 用于存储待创建二叉树中所有值的字符数组
* @return 返回根节点
*/
public static Node createBinaryTree(char[] arr) {
Node root = null;
for (int i = 0; i < arr.length; i++) {
Node newNode = null;
if (root == null) {
root = new Node(null, null, arr[i]);
continue;
}
if (!contains(root, arr[i])) {
newNode = new Node(null, null, arr[i]);
insertBinaryTreeNode(root, newNode);
}
}
return root;
}
/**
* 判断二叉树中是否包含指定字符
* @param root 根节点
* @param c 待判断字符
* @return
*/
public static boolean contains(Node root, char c) {
Queue<Node> queue = new ArrayBlockingQueue<Node>(10);
queue.offer(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
if (node != null) {
if (node.data == c) {
return true;
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
return false;
}
/**
* 通过BFS方式向二叉树中插入节点
* @param root 根节点
* @param c 待插入节点的值
*/
public static boolean insertBinaryTreeNode(Node root, char c) {
if (!contains(root, c)) {
Node newNode = new Node(null, null, c);
return insertBinaryTreeNode(root, newNode);
}
return false;
}
/**
* 通过BFS方式向二叉树中插入节点
* @param root 根节点
* @param node 待插入节点
*/
public static boolean insertBinaryTreeNode(Node root, Node node) {
Queue<Node> queue = new ArrayBlockingQueue<Node>(10);
queue.offer(root);
while (!queue.isEmpty()) {
Node temp = queue.poll();
if (temp != null) {
if (temp.left == null) {
temp.left = node;
// 记住,这里是插入节点,一旦插入成功就直接返回,不用再循环
return true;
} else {
if (temp.right == null) {
temp.right = node;
// 记住,这里是插入节点,一旦插入成功就直接返回,不用再循环
return true;
} else {
// 将左右孩子都入队
queue.offer(temp.left);
queue.offer(temp.right);
}
}
}
}
return false;
}
/**
* 深度优先遍历
* 递归实现
* @param root 根节点
*/
public static void dfsDivision(Node root) {
if (root == null) {
return;
}
System.out.print(root.data + "\t");
dfsDivision(root.left);
dfsDivision(root.right);
}
/**
* 深度优先遍历
* 迭代实现
* @param root
*/
public static void dfsIterator(Node root) {
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
root = stack.pop();
if (root != null) {
System.out.print(root.data + "\t");
// 先将右孩子入栈,这里是跟广度优先遍历中的队列入队刚好相反
if (root.right != null) {
stack.push(root.right);
}
if (root.left != null) {
stack.push(root.left);
}
}
}
}
/**
* 广度优先遍历:广度优先遍历,也可以称为层次优先遍历,从上到下,先把每一层遍历完之后再遍历一下一层
* @param root 根节点
*/
public static void bfs(Node root) {
Queue<Node> queue = new ArrayBlockingQueue<Node>(10);
queue.offer(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
if (node != null) {
System.out.print(node.data + "\t");
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
}
}
四、测试类
public class Test {
public static void main(String[] args) {
char[] cArr = new char[]{
'B',
'F',
'A',
'C',
'E',
'G',
'D'};
Node root = BTreeUtil.createBinaryTree(cArr);
System.out.println("深度优先遍历");
BTreeUtil.dfsIterator(root);
System.out.println();
System.out.println("广度优先遍历");
BTreeUtil.bfs(root);
}
}
五、运行结果
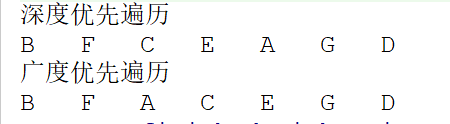









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· DeepSeek在M芯片Mac上本地化部署
· 葡萄城 AI 搜索升级:DeepSeek 加持,客户体验更智能