快速幂——步步演化

快速幂运算，提高算法效率的绝佳选择
我们首先来了解一下“取模”运算的运算法则：（具体的证明感兴趣的同学可以问度娘）

(a + b) % p = (a % p + b % p) % p （1）

(a - b) % p = (a % p - b % p ) % p （2）

(a * b) % p = (a % p * b % p) % p （3）

其中我们只要关注第“3”条法则即可：(a * b) % p = (a % p * b % p) % p ，我们仔细研究一下这个运算法则，会发现多个因子连续的乘积取模的结果等于每个因子取模后的乘积再取模的结果。也就是说，我们如果要求：

(abc)%d=(a%db%dc%d)%d;

因此，我们可以借助这个法则，只需要在循环乘积的每一步都提前进行“取模”运算，而不是等到最后直接对结果“取模”，也能达到同样的效果。
Java代码如下

package com.lzp.util;

/**
 * @Author LZP
 * @Date 2021/2/21 8:21
 * @Version 1.0
 *
 * 快速幂
 */
public class QuickPow {

    /**
     * 求底数为a，指数为n的幂
     * 效率极低，而且结果不能表示出来
     * @param a 底数
     * @param n 指数
     */
    @Deprecated
    public static long pow(long a, long n) {
        if (a == 0) {
            System.out.println("幂运算的底数不能为0");
        }
        if (a == 1) {
            return 1;
        }
        if (n == 0) {
            return 1;
        }
        if (n == 1) {
            return a;
        }

        long result = 1;
        for (int i = 0; i < n; i++) {
            result *= a;
        }

        return result;
    }

    /**
     * 求底数为a，指数为n的幂
     * 加上一个求模的数，是为了防止指数的爆炸式增长会超出我们目前计算机中数的表示范围
     * 效率还是较低，但结果能表示出来
     * @param a 底数
     * @param n 指数
     * @param mod 模
     */
    public static long pow(long a, long n, long mod) {
        if (a == 0) {
            System.out.println("幂运算的底数不能为0");
        }
        if (a == 1) {
            return 1;
        }
        if (n == 0) {
            return 1;
        }
        if (n == 1) {
            return a;
        }

        long result = 1;
        for (int i = 0; i < n; i++) {
            result *= a;
            result %= mod;
        }

        return result % mod;
    }

    /**
     * 快速幂
     * 求底数为a，指数为n的幂
     * 加上一个求模的数，是为了防止指数的爆炸式增长会超出我们目前计算机中数的表示范围
     * 效率明显提高，且结果能表示出来
     * @param a 底数
     * @param n 指数
     * @param mod 模
     */
    public static long qPow(long a, long n, long mod) {
        if (a == 0) {
            System.out.println("幂运算的底数不能为0");
        }
        if (a == 1) {
            return 1;
        }
        if (n == 0) {
            return 1;
        }
        if (n == 1) {
            return a;
        }

        long result = 1;
        while (n > 0) {
            if (n % 2 == 0) {
                // 缩指数操作后：数的结果跟原来数的结果一模一样
                // 指数为偶数
                // 可以缩指数，即对半缩，指数缩小一半，底数扩大一倍（即为原来底数的两倍）
                n = n >> 1;
                a *= a;
                a %= mod;
            } else {
                // 指数为奇数
                n = n - 1;
                // 把当前底数累乘到result临时变量中，因为每次底数都在变化
                result *= a;
                result %= mod;
                // 如果此时n已经为0，后面的a就再也不会被累乘到result中了，即可以跳出循环
                n = n >> 1;
                a *= a;
                a %= mod;
            }
        }

        return result % mod;
    }

    /**
     * 优化快速幂
     * 求底数为a，指数为n的幂
     * 加上一个求模的数，是为了防止指数的爆炸式增长会超出我们目前计算机中数的表示范围
     * 效率明显提高，且结果能表示出来
     * @param a 底数
     * @param n 指数
     * @param mod 模
     */
    public static long qPowPlus(long a, long n, long mod) {
        if (a == 0) {
            System.out.println("幂运算的底数不能为0");
        }
        if (a == 1) {
            return 1;
        }
        if (n == 0) {
            return 1;
        }
        if (n == 1) {
            return a;
        }

        long result = 1;
        while (n > 0) {
            if (n % 2 == 1) {
                // 指数为奇数
                n = n - 1;
                // 把当前底数累乘到result临时变量中，因为每次底数都在变化
                result *= a;
                result %= mod;
            }
            // 缩指数操作后：数的结果跟原来数的结果一模一样
            // 指数为偶数
            // 可以缩指数，即对半缩，指数缩小一半，底数扩大一倍（即为原来底数的两倍）
            // 如果此时n已经为0，后面的a就再也不会被累乘到result中了，即可以跳出循环
            n = n >> 1;
            a *= a;
            // 注意：底数也要求模
            a %= mod;
        }

        return result % mod;
    }
}

测试数据

package com.lzp.test.day12;

import com.lzp.util.QuickPow;

/**
 * @Author LZP
 * @Date 2021/2/21 9:05
 * @Version 1.0
 */
public class QuickPowTestTime {
    public static void main(String[] args) {

        System.out.println("============测试时间============");
        System.out.println("===========没有用快速幂============");
        long start = System.currentTimeMillis();
        System.out.println(QuickPow.pow(2, 1000000000, 1000));
        long end = System.currentTimeMillis();
        System.out.println(end - start + "ms");

        System.out.println("=============用快速幂==============");
        long start2 = System.currentTimeMillis();
        System.out.println(QuickPow.qPow(2, 1000000000, 1000));
        long end2 = System.currentTimeMillis();
        System.out.println(end2 - start2 + "ms");

        System.out.println("=============用快速幂优化版==============");
        long start3 = System.currentTimeMillis();
        System.out.println(QuickPow.qPowPlus(2, 1000000000, 1000));
        long end3 = System.currentTimeMillis();
        System.out.println(end3 - start3 + "ms");

    }
}

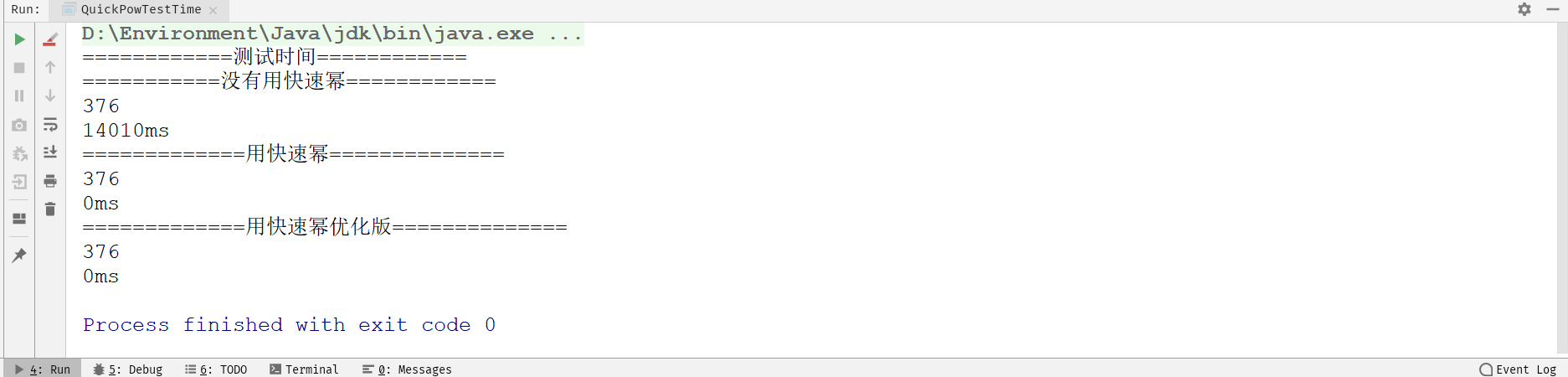
运行结果