数据挖据之GeoHash核心原理解析
引子
机机是个好动又好学的孩子,平日里就喜欢拿着手机地图点点按按来查询一些好玩的东西。某一天机机到北海公园游玩,肚肚饿了,于是乎打开手机地图,搜索北海公园附近的餐馆,并选了其中一家用餐。
饭饱之后机机开始反思了,地图后台如何根据自己所在位置查询来查询附近餐馆的呢?苦思冥想了半天,机机想出了个方法:计算所在位置P与北京所有餐馆的距离,然后返回距离<=1000米的餐馆。小得意了一会儿,机机发现北京的餐馆何其多啊,这样计算不得了,于是想了,既然知道经纬度了,那它应该知道自己在西城区,那应该计算所在位置P与西城区所有餐馆的距离啊,机机运用了递归的思想,想到了西城区也很多餐馆啊,应该计算所在位置P与所在街道所有餐馆的距离,这样计算量又小了,效率也提升了。
机机的计算思想很朴素,就是通过过滤的方法来减小参与计算的餐馆数目,从某种角度上讲,机机在使用索引技术。
一提到索引,大家脑子里马上浮现出B树索引,因为大量的数据库(如MySQL、oracle、PostgreSQL等)都在使用B树。B树索引本质上是对索引字段进行排序,然后通过类似二分查找的方法进行快速查找,即它要求索引的字段是可排序的,一般而言,可排序的是一维字段,比如时间、年龄、薪水等等。但是对于空间上的一个点(二维,包括经度和纬度),如何排序呢?又如何索引呢?解决的方法很多,下文介绍一种方法来解决这一问题。
思想:如果能通过某种方法将二维的点数据转换成一维的数据,那样不就可以继续使用B树索引了嘛。那这种方法真的存在嘛,答案是肯定的。目前很火的GeoHash算法就是运用了上述思想,下面我们就开始GeoHash之旅吧。
一、感性认识GeoHash
首先来点感性认识,http://openlocation.org/geohash/geohash-js/ 提供了在地图上显示geohash编码的功能。
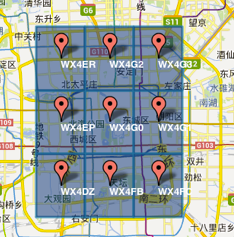
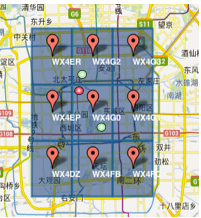
1)GeoHash将二维的经纬度转换成字符串,比如下图展示了北京9个区域的GeoHash字符串,分别是WX4ER,WX4G2、WX4G3等等,每一个字符串代表了某一矩形区域。也就是说,这个矩形区域内所有的点(经纬度坐标)都共享相同的GeoHash字符串,这样既可以保护隐私(只表示大概区域位置而不是具体的点),又比较容易做缓存,比如左上角这个区域内的用户不断发送位置信息请求餐馆数据,由于这些用户的GeoHash字符串都是WX4ER,所以可以把WX4ER当作key,把该区域的餐馆信息当作value来进行缓存,而如果不使用GeoHash的话,由于区域内的用户传来的经纬度是各不相同的,很难做缓存。
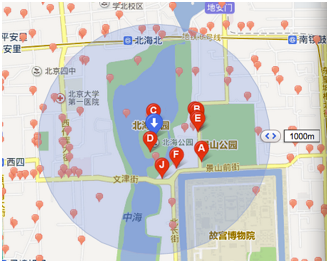
2)字符串越长,表示的范围越精确。如图所示,5位的编码能表示10平方千米范围的矩形区域,而6位编码能表示更精细的区域(约0.34平方千米)
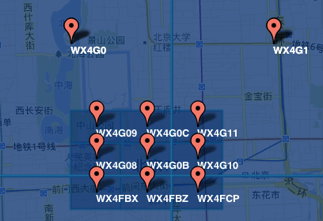
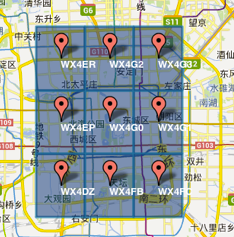
3)字符串相似的表示距离相近(特殊情况后文阐述),这样可以利用字符串的前缀匹配来查询附近的POI信息。如下两个图所示,一个在城区,一个在郊区,城区的GeoHash字符串之间比较相似,郊区的字符串之间也比较相似,而城区和郊区的GeoHash字符串相似程度要低些。
|
城区 |
郊区 |
通过上面的介绍我们知道了GeoHash就是一种将经纬度转换成字符串的方法,并且使得在大部分情况下,字符串前缀匹配越多的距离越近,回到我们的案例,根据所在位置查询来查询附近餐馆时,只需要将所在位置经纬度转换成GeoHash字符串,并与各个餐馆的GeoHash字符串进行前缀匹配,匹配越多的距离越近。
二、GeoHash算法的步骤
下面以北海公园为例介绍GeoHash算法的计算步骤

2.1. 根据经纬度计算GeoHash二进制编码
地球纬度区间是[-90,90], 北海公园的纬度是39.928167,可以通过下面算法对纬度39.928167进行逼近编码:
1)区间[-90,90]进行二分为[-90,0),[0,90],称为左右区间,可以确定39.928167属于右区间[0,90],给标记为1;
2)接着将区间[0,90]进行二分为 [0,45),[45,90],可以确定39.928167属于左区间 [0,45),给标记为0;
3)递归上述过程39.928167总是属于某个区间[a,b]。随着每次迭代区间[a,b]总在缩小,并越来越逼近39.928167;
4)如果给定的纬度x(39.928167)属于左区间,则记录0,如果属于右区间则记录1,这样随着算法的进行会产生一个序列1011100,序列的长度跟给定的区间划分次数有关。
根据纬度算编码
|
bit |
min |
mid |
max |
|
1 |
-90.000 |
0.000 |
90.000 |
|
0 |
0.000 |
45.000 |
90.000 |
|
1 |
0.000 |
22.500 |
45.000 |
|
1 |
22.500 |
33.750 |
45.000 |
|
1 |
33.7500 |
39.375 |
45.000 |
|
0 |
39.375 |
42.188 |
45.000 |
|
0 |
39.375 |
40.7815 |
42.188 |
|
0 |
39.375 |
40.07825 |
40.7815 |
|
1 |
39.375 |
39.726625 |
40.07825 |
|
1 |
39.726625 |
39.9024375 |
40.07825 |
同理,地球经度区间是[-180,180],可以对经度116.389550进行编码。
根据经度算编码
|
bit |
min |
mid |
max |
|
1 |
-180 |
0.000 |
180 |
|
1 |
0.000 |
90 |
180 |
|
0 |
90 |
135 |
180 |
|
1 |
90 |
112.5 |
135 |
|
0 |
112.5 |
123.75 |
135 |
|
0 |
112.5 |
118.125 |
123.75 |
|
1 |
112.5 |
115.3125 |
118.125 |
|
0 |
115.3125 |
116.71875 |
118.125 |
|
1 |
115.3125 |
116.015625 |
116.71875 |
|
1 |
116.015625 |
116.3671875 |
116.71875 |
2.2. 组码
通过上述计算,纬度产生的编码为10111 00011,经度产生的编码为11010 01011。偶数位放经度,奇数位放纬度,把2串编码组合生成新串:11100 11101 00100 01111。
最后使用用0-9、b-z(去掉a, i, l, o)这32个字母进行base32编码,首先将11100 11101 00100 01111转成十进制,对应着28、29、4、15,十进制对应的编码就是wx4g。同理,将编码转换成经纬度的解码算法与之相反,具体不再赘述。

三、GeoHash Base32编码长度与精度
下表摘自维基百科:http://en.wikipedia.org/wiki/Geohash
可以看出,当geohash base32编码长度为8时,精度在19米左右,而当编码长度为9时,精度在2米左右,编码长度需要根据数据情况进行选择。

三、GeoHash算法
上文讲了GeoHash的计算步骤,仅仅说明是什么而没有说明为什么?为什么分别给经度和维度编码?为什么需要将经纬度两串编码交叉组合成一串编码?本节试图回答这一问题。
如图所示,我们将二进制编码的结果填写到空间中,当将空间划分为四块时候,编码的顺序分别是左下角00,左上角01,右下脚10,右上角11,也就是类似于Z的曲线,当我们递归的将各个块分解成更小的子块时,编码的顺序是自相似的(分形),每一个子快也形成Z曲线,这种类型的曲线被称为Peano空间填充曲线。
这种类型的空间填充曲线的优点是将二维空间转换成一维曲线(事实上是分形维),对大部分而言,编码相似的距离也相近, 但Peano空间填充曲线最大的缺点就是突变性,有些编码相邻但距离却相差很远,比如0111与1000,编码是相邻的,但距离相差很大。
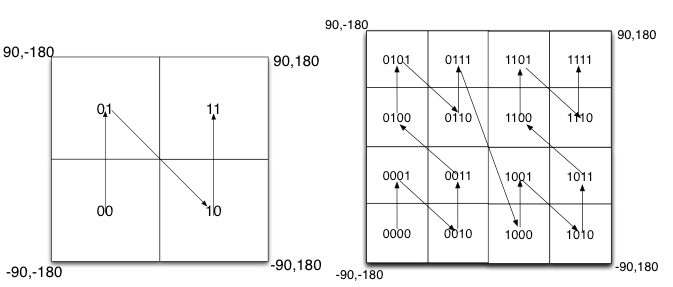
除Peano空间填充曲线外,还有很多空间填充曲线,如图所示,其中效果公认较好是Hilbert空间填充曲线,相较于Peano曲线而言,Hilbert曲线没有较大的突变。为什么GeoHash不选择Hilbert空间填充曲线呢?可能是Peano曲线思路以及计算上比较简单吧,事实上,Peano曲线就是一种四叉树线性编码方式。

四、使用注意点
1)由于GeoHash是将区域划分为一个个规则矩形,并对每个矩形进行编码,这样在查询附近POI信息时会导致以下问题,比如红色的点是我们的位置,绿色的两个点分别是附近的两个餐馆,但是在查询的时候会发现距离较远餐馆的GeoHash编码与我们一样(因为在同一个GeoHash区域块上),而较近餐馆的GeoHash编码与我们不一致。这个问题往往产生在边界处。
解决的思路很简单,我们查询时,除了使用定位点的GeoHash编码进行匹配外,还使用周围8个区域的GeoHash编码,这样可以避免这个问题。
2)我们已经知道现有的GeoHash算法使用的是Peano空间填充曲线,这种曲线会产生突变,造成了编码虽然相似但距离可能相差很大的问题,因此在查询附近餐馆时候,首先筛选GeoHash编码相似的POI点,然后进行实际距离计算。
参考文献:
http://en.wikipedia.org/wiki/Geohash
http://openlocation.org/geohash/geohash-js/
Cantor空間填充曲線之演算法探討.pdf
http://www.cnblogs.com/LBSer/p/3310455.html
http://blog.csdn.net/wangxiafghj/article/details/9014363