webgl 系列 —— 变换矩阵和动画
其他章节请看:
变换矩阵和动画
动画就是不停地将某个东西变换(transform)。例如将三角形不停地旋转就是一个动画
和 CSS transform 类似,变换有三种形式:平移、缩放和旋转。
简单的变换用普通表达式容易实现,如果事情复杂,比如旋转后平移,这时就可以使用变换矩阵。
普通表达式
平移
比如要平移一个三角形,只需要将三个顶点移动相同的距离即可(这是一个逐顶点操作)

用二维向量表示,就像这样:[x1, y1] + [tx1, ty2] = [x2, y2]
比如要实现如下效果:

前面我们已经讲过三角形了,这里不再冗余,改动的核心代码如下:
const VSHADER_SOURCE = `
attribute vec4 a_Position;
+uniform vec4 u_Translation;
void main() {
- gl_Position = a_Position;
+ gl_Position = a_Position + u_Translation;
gl_PointSize = 10.0;
}
`
function main() {
gl.clearColor(0, 0, 0, 1);
gl.clear(gl.COLOR_BUFFER_BIT);
+ const u_Translation = gl.getUniformLocation(gl.program, 'u_Translation');
+ if (!u_Translation) {
+ return;
+ }
+ gl.uniform4f(u_Translation, 0.5, 0.5, 0, 0.0);
+
a_Position 和 u_Translation 都是 vec4 类型,使用 + 号,两个矢量(也称向量)对应的分量会被同时相加(矢量相加是着色器语言的特性之一)。就像这样:
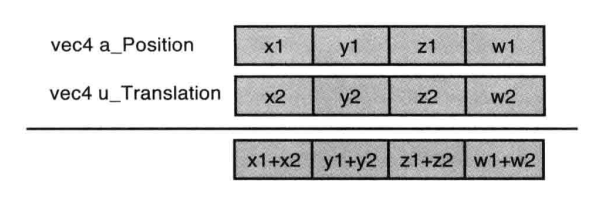
缩放
以一个点为例,比如要将 A 点缩放到 B 点,乘以一个系数就好,系数小于1表示缩小,系数大于1表示放大:
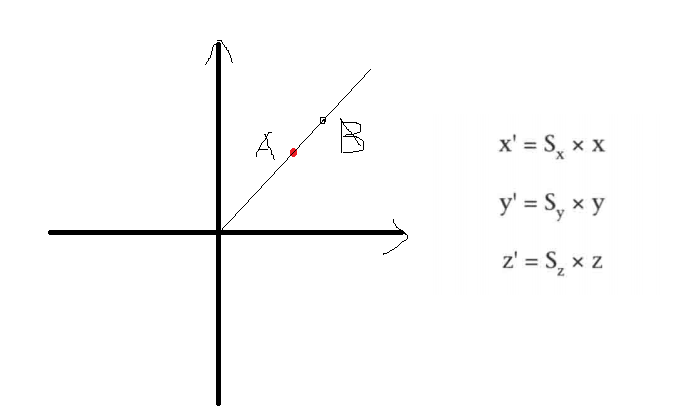
用二维向量表示,就像这样:k[x1, y1] = [x2, y2]
旋转
比如要将 p 点旋转 β,推导出来的公式如下:
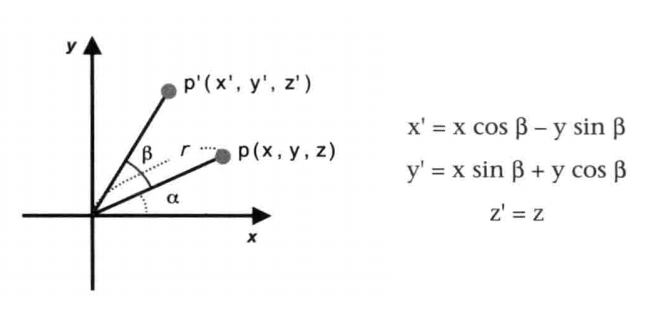
变换矩阵
概念
变换矩阵(非常适合操作计算机图形)是数学线性代数中的一个概念。请看下图:
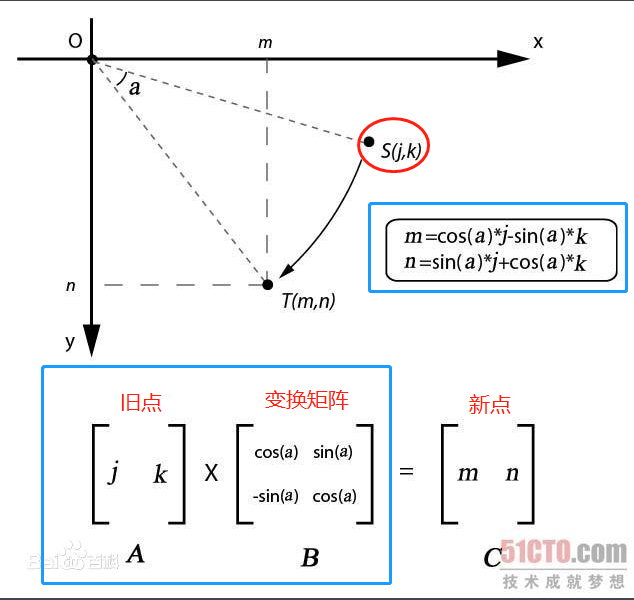
将点从 S 旋转到 T,新坐标(m, n)可以用普通表达式表示,同样可以用变换矩阵来表示(旧点 * 变换矩阵 = 新点)
变换矩阵和向量相乘有一个规则,并会得到一个新的向量。
Tip:webgl 中的一个点,在坐标系中就相当于一个向量
在 webgl 中变换矩阵和向量相乘的规则如下:

注:牢记公式:变换矩阵 * 向量 会生成一个新的向量;顺序不同结果也不同,例如:向量 * 变换矩阵
旋转
将旋转的普通表达式转为变换矩阵:
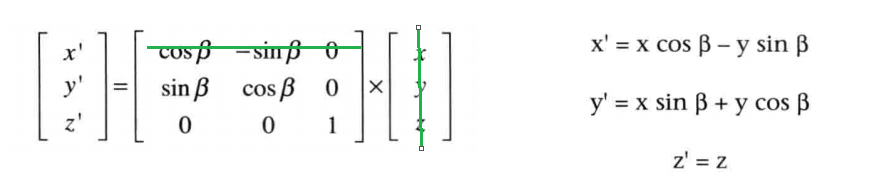
四维矩阵
为什么要用四维矩阵?
因为三维矩阵矩阵不够用,比如将 (0,0,0) 移动到 (1, 0, 0),用三维矩阵是表示不出来的,而四维却可以。请看下图:
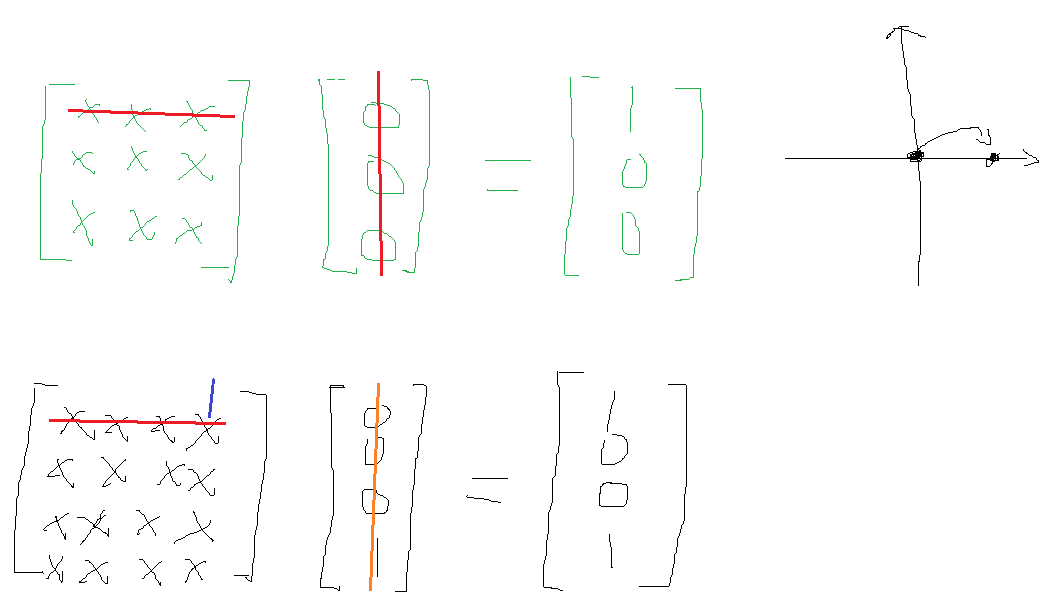
平移
将平移的普通表达式转为变换矩阵:

缩放
将缩放的普通表达式转为变换矩阵:

手动矩阵
为了更好的理解矩阵。我们先不使用矩阵库,直接通过 js 来使用矩阵实现变换。
矩阵颠倒
js 中没有矩阵数据类型,这里用数组表示。
比如要表示如下一个平移矩阵:
1, 0, 0, Tx
0, 1, 0, Ty
0, 0, 1, Tz
0, 0, 0, 1
数组就是这样:
const matrix = [
1, 0, 0, Tx,
0, 1, 0, Ty,
0, 0, 1, Tz,
0, 0, 0, 1,
]
而要表示如上这个变换矩阵,在 webgl 中就得将数组颠倒:行变成列。
所以最后就得这么写:
const matrix = [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
Tx, Ty, Tz, 1,
]
Tip: 对于缩放,颠倒后和颠倒前是相同的。
平移
需求:将三角形向右上角偏移。
效果:

前面我们已经学会画三角形,笔者在此基础上改动如下代码:
const VSHADER_SOURCE = `
+// mat4 是一种4维矩阵
+uniform mat4 u_xformMatrix;
void main() {
- gl_Position = a_Position ;
+ // 注:必须是 "变换矩阵 * 向量",不可是 "向量 * 变换矩阵"
+ gl_Position = u_xformMatrix * a_Position ;
gl_PointSize = 10.0;
}
`
function main() {
initVertexBuffers(gl, vertices)
+ 变换(gl)
gl.drawArrays(gl.TRIANGLES, 0, vertices.vertexNumber);
}
+function 变换(gl){
+ const u_xformMatrix = gl.getUniformLocation(gl.program, 'u_xformMatrix');
+ if (!u_xformMatrix) {
+ console.log('Failed to get the storage location of u_xformMatrix');
+ return;
+ }
+ // 四维矩阵
+ const [Tx, Ty, Tz] = [0.5, 0.5, 0];
+ // webgl 中矩阵的行和列是要颠倒的,比如要传一个 A 矩阵,给 webgl 的A矩阵就得颠倒,也就是将 A 的第一行变为第一列,第二行变成第二列
+ const matrix = new Float32Array([
+ 1, 0, 0, 0,
+ 0, 1, 0, 0,
+ 0, 0, 1, 0,
+ Tx, Ty, Tz, 1,
+ ])
+ // 将矩阵分配给 u_xformMatrix
+ gl.uniformMatrix4fv(u_xformMatrix, false, matrix);
+}
代码解析:
- 前面已经说过,变换是一个
逐顶点的操作,每个顶点都相同,所以不用 attribute 而用 uniform mat4表示4*4的矩阵- 向量(新点) =
变换矩阵* 向量(旧点) - gl.uniformMatrix4fv(location, transpose, value) 为 uniform variables 指定矩阵值。webgl 中 transpose 必须为 false.
注:如果改变变换矩阵 * 向量的顺序,平移效果就不对了:
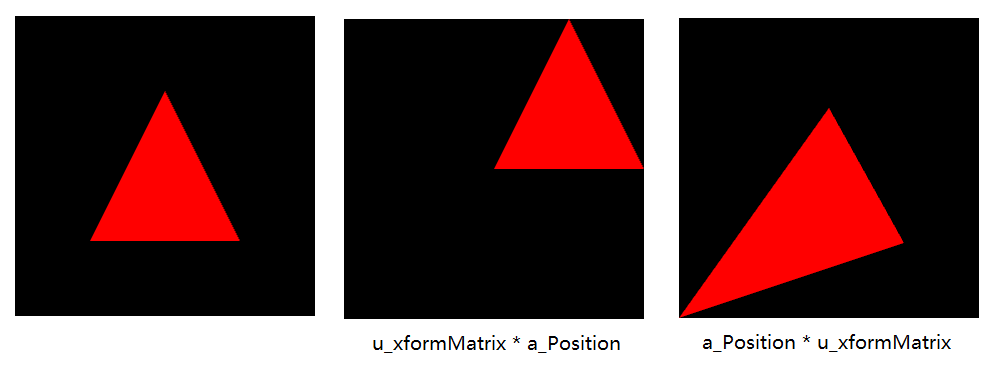
矩阵库
自己手写矩阵数组非常麻烦。
openGL 提供了一系列有用的函数帮助我们创建变换矩阵。例如通过 glTranslate 传入在 x、y、z 上平移的距离,就可以创建一个平移矩阵。
既然 webgl 中未提供创建变换矩阵的函数,我们就使用库来做这部分工作。
gl-matrix
笔者使用一个较流行的矩阵库 gl-matrix —— 用于高性能WebGL应用程序的Javascript矩阵和矢量(又称为向量)库。
下载后,在 dist 目录下看到 esm 文件夹和两个 js 文件:
toji-gl-matrix-4480752/dist (master)
$ ll
drwxr-xr-x 1 Administrator 197121 0 Mar 6 15:26 esm/
-rw-r--r-- 1 Administrator 197121 52466 Jan 10 05:24 gl-matrix-min.js
-rw-r--r-- 1 Administrator 197121 206643 Jan 10 05:24 gl-matrix.js
其实也就是提供两种使用的方法:
- esm 通过
<script type="module" src="main.mjs"></script>这种方式使用 - 最常见的
<script src="animation.js"></script>
笔者选用第二种:在 html 中引入:<script src="./animation.js"></script>
这时在控制台就有一个 glMatrix 全局变量:
glMatrix
{glMatrix: {…}, mat2: {…}, mat2d: {…}, mat3: {…}, mat4: {…}, …}
glMatrix: {EPSILON: 0.000001, ANGLE_ORDER: "zyx", RANDOM: ƒ, setMatrixArrayType: ƒ, …}
mat2: {create: ƒ, clone: ƒ, copy: ƒ, identity: ƒ, fromValues: ƒ, …}
mat2d: {create: ƒ, clone: ƒ, copy: ƒ, identity: ƒ, fromValues: ƒ, …}
mat3: {create: ƒ, fromMat4: ƒ, clone: ƒ, copy: ƒ, fromValues: ƒ, …}
mat4: {create: ƒ, clone: ƒ, copy: ƒ, fromValues: ƒ, set: ƒ, …}
quat: {create: ƒ, identity: ƒ, setAxisAngle: ƒ, getAxisAngle: ƒ, getAngle: ƒ, …}
quat2: {create: ƒ, clone: ƒ, fromValues: ƒ, fromRotationTranslationValues: ƒ, fromRotationTranslation: ƒ, …}
vec2: {create: ƒ, clone: ƒ, fromValues: ƒ, copy: ƒ, set: ƒ, …}
vec3: {create: ƒ, clone: ƒ, length: ƒ, fromValues: ƒ, copy: ƒ, …}
vec4: {create: ƒ, clone: ƒ, fromValues: ƒ, copy: ƒ, set: ƒ, …}
官方文档也是从这几个模块来介绍的:mat2, mat2d, mat3, mat4, quat, quat2, vec2, vec3, vec4。
mat[234]就是2维3维4维矩阵vec[234]就是2维3维4维向量
四维矩阵
首先取得 mat4 模块,然后调用 create() 就会创建一个四维矩阵:
// 四维矩阵模块
const { mat4 } = glMatrix
// 创建一个4维单位矩阵
const matrix = mat4.create()
/*
Float32Array(16) [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1]
*/
console.log(matrix)
Tip: create() 创建的是一个单位矩阵,如同数的乘法中的1
平移矩阵
fromTranslation - 平移矩阵
语法如下:
(static) fromTranslation(out, v) → {mat4}
Creates a matrix from a vector translation This is equivalent to (but much faster than): mat4.identity(dest); mat4.translate(dest, dest, vec);
Parameters:
Name Type Description
out mat4 mat4 receiving operation result
v ReadonlyVec3 Translation vector
Returns:
out
请看示例:
mat4.fromTranslation(matrix, [0.5, 0.5, 0])
/*
Float32Array(16) [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0.5, 0.5, 0, 1
]
*/
console.log(matrix)
matrix 是一个单位矩阵,通过该方法,即可得到一个向 x 和 y 各平移 0.5 的变换矩阵。
与之对应不修改原矩阵的方法是:translate(out, a, v)。语法如下:
(static) translate(out, a, v) → {mat4}
Translate a mat4 by the given vector
Parameters:
Name Type Description
out mat4 the receiving matrix
a ReadonlyMat4 the matrix to translate
v ReadonlyVec3 vector to translate by
Returns:
out
请看示例:
const matrix2 = mat4.create()
mat4.translate(matrix2, matrix, [0.5, 0.5, 0])
// Float32Array(16) [1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1]
/*
Float32Array(16) [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
]
*/
console.log(matrix)
/*
Float32Array(16) [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0.5, 0.5, 0, 1
]
*/
console.log(matrix2)
matrix 没有改变,最终变换矩阵输出到 matrix2。
旋转矩阵
fromRotation - 旋转矩阵
创建一个旋转矩阵。请看示例:
// fromRotation(out, rad, axis) - out 是要修改的矩阵、rad 旋转角度、axis 围绕哪个轴旋转 [x, y, z]
const angle = 90
// 角度转弧度
const rad = angle * Math.PI / 180;
const axis = [0, 0, 1];
// 等于 fromXRotation、fromYRotation、fromZRotation
mat4.fromRotation(matrix, rad, axis)
/*
Float32Array(16) [
6.123234262925839e-17, 1, 0, 0,
-1, 6.123234262925839e-17, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
]
*/
console.log(matrix)
与之对应不修改原矩阵的方法是:rotate(out, a, rad, axis)。用法与平移中的类似。
toRadian
旋转矩阵需要使用弧度,通过 toRadian() 可以将角度转为弧度。用法如下:
glMatrix.glMatrix.toRadian(180) => 3.141592653589793
缩放矩阵
fromScaling - 缩放矩阵
创建一个缩放矩阵。请看示例:
mat4.fromScaling(matrix, [2, 2, 0])
/*
Float32Array(16) [
2, 0, 0, 0,
0, 2, 0, 0,
0, 0, 0, 0,
0, 0, 0, 1
]
*/
console.log(matrix)
与之对应不修改原矩阵的方法是:scale(out, a, v)。用法与平移中的类似。
平移
现在使用这个库来实现平移,只需要将手动矩阵替换如下即可:
- const matrix = new Float32Array([
- 1, 0, 0, 0,
- 0, 1, 0, 0,
- 0, 0, 1, 0,
- Tx, Ty, Tz, 1,
- ])
+
+ const { mat4 } = glMatrix
+ const matrix = mat4.create()
+ mat4.fromTranslation(matrix, [Tx, Ty, 0])
旋转、缩放也类似,不再展开。
组合变换矩阵
变换矩阵可以组合,比如希望将三角形旋转和平移,这里需要注意:顺序不同导致结果不同。请看下图

核心代码:
const VSHADER_SOURCE = `
attribute vec4 a_Position;
// 移动矩阵
uniform mat4 u_tformMatrix;
// 旋转矩阵
uniform mat4 u_rformMatrix;
void main() {
// 先旋转后移动
// gl_Position = u_tformMatrix * u_rformMatrix * a_Position;
// 先移动后旋转
gl_Position = u_rformMatrix * u_tformMatrix * a_Position;
gl_PointSize = 10.0;
}
`
const u_rformMatrix = gl.getUniformLocation(gl.program, 'u_rformMatrix');
const u_tformMatrix = gl.getUniformLocation(gl.program, 'u_tformMatrix');
const { mat4 } = glMatrix
const tMatrix = mat4.create()
const rMatrix = mat4.create()
mat4.fromTranslation(tMatrix, [0.5, 0, 0])
// 设置移动矩阵
gl.uniformMatrix4fv(u_tformMatrix, false, tMatrix);
const rad = glMatrix.glMatrix.toRadian(90)
const axis = [0, 0, 1];
mat4.fromRotation(rMatrix, rad, axis)
// 设置旋转矩阵
gl.uniformMatrix4fv(u_rformMatrix, false, rMatrix);
组合变换矩阵的顺序和 css 类似,从右往左。比如:
u_rformMatrix * u_tformMatrix * a_Position先移动后旋转u_tformMatrix * u_rformMatrix * a_Position先旋转后移动
Tip: 这里的组合变换矩阵其实就是计算机图形学中模型变换(M)。还有视图变换(V)、投影变换(P),统称为 MVP。
动画
需求
需求:绘制一个旋转动画
效果如下:

实现
思路:
- 首先绘制三角形
- 通过变换矩阵进行旋转
- 不停的绘制(改变旋转角度)。使用专门用于动画的requestAnimationFrame(用法类似 setTimeout,但不需要指定回调时间,浏览器会在最恰当的时候回调)
完整代码如下:
const VSHADER_SOURCE = `
attribute vec4 a_Position;
// 所有顶点移动位置都相同,所以不用 Attribute 而用 uniform
// mat4 是一种4维矩阵
uniform mat4 u_xformMatrix;
void main() {
// 注:必须是 "变换矩阵 * 向量",不可是 "向量 * 变换矩阵"
gl_Position = u_xformMatrix * a_Position ;
gl_PointSize = 10.0;
}
`
const FSHADER_SOURCE = `
void main() {
gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);
}
`
function main() {
const canvas = document.getElementById('webgl');
const gl = canvas.getContext("webgl");
if (!gl) {
console.log('Failed to get the rendering context for WebGL');
return;
}
if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
console.log('Failed to intialize shaders.');
return;
}
const vertices = {
data: new Float32Array([
0.0, 0.5,
-0.5, -0.5,
0.5, -0.5
]),
vertexNumber: 3,
count: 2,
}
initVertexBuffers(gl, vertices)
tick(gl, vertices)
}
function initVertexBuffers(gl, { data, count }) {
// 1. 创建缓冲区对象
const vertexBuffer = gl.createBuffer();
if (!vertexBuffer) {
console.log('创建缓冲区对象失败');
return -1;
}
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
const a_Position = gl.getAttribLocation(gl.program, 'a_Position');
if (a_Position < 0) {
console.log('Failed to get the storage location of a_Position');
return -1;
}
gl.vertexAttribPointer(a_Position, count, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(a_Position);
}
function 变换(gl, vertices) {
const u_xformMatrix = gl.getUniformLocation(gl.program, 'u_xformMatrix');
if (!u_xformMatrix) {
console.log('Failed to get the storage location of u_xformMatrix');
return;
}
const { mat4 } = glMatrix
const matrix = mat4.create()
const rad = glMatrix.glMatrix.toRadian(angle)
const axis = [0, 0, 1];
mat4.fromRotation(matrix, rad, axis)
gl.uniformMatrix4fv(u_xformMatrix, false, matrix);
gl.clearColor(0, 0, 0, 1);
gl.clear(gl.COLOR_BUFFER_BIT);
gl.drawArrays(gl.TRIANGLES, 0, vertices.vertexNumber);
}
let angle = 0
// 每次改变的角度
const seed = 1
function tick(gl, vertices){
变换(gl, vertices)
// 改变角度
angle += seed;
// 动画绘制
requestAnimationFrame(() => tick(gl, vertices))
}
其他章节请看:
出处:https://www.cnblogs.com/pengjiali/p/17200893.html
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接。


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步