【训练1】2.24.4.13美团春招
前言
写在前面,由于很长一段时间没有敲代码了,上周写了华为的题目,debug半天也没有debug出一道来,属实狠狠的打击到我了,因此特开此专栏,以便开启老年选手康复之路!!!
第一题-塔子哥的好子矩阵
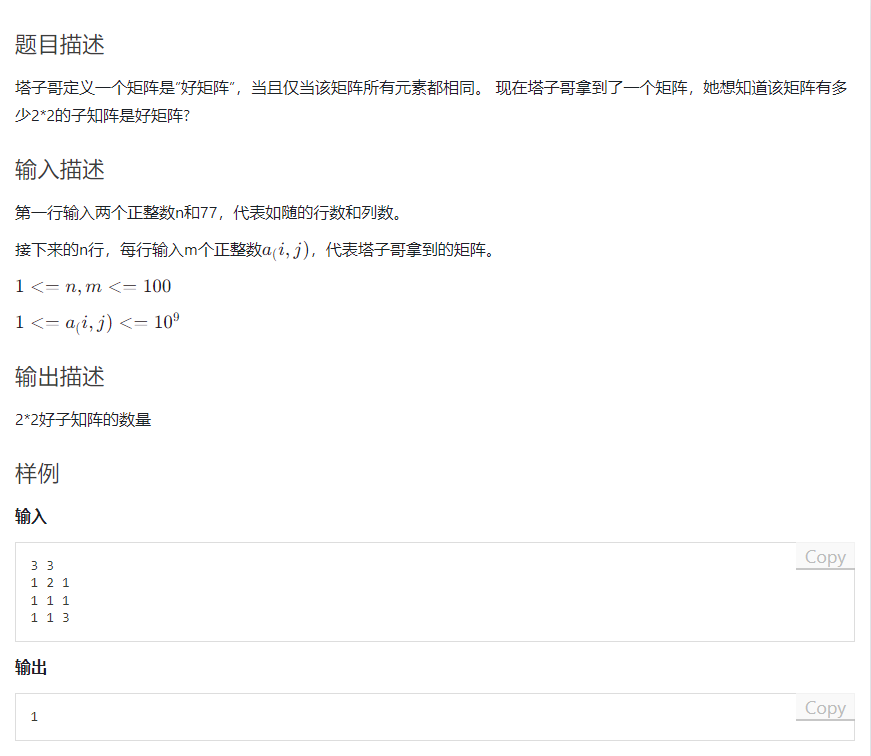
前3题,手速题
水题
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 666;
int n,m,arr[N][N];
signed main(){
cin>>n>>m;
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>arr[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if((i+1)>n||(j+1)>m) continue;
int a=arr[i][j];
int b=arr[i+1][j+1];
int c=arr[i+1][j];
int d=arr[i][j+1];
if(a==b&&b==c&&d==c&&a==d) ans++;
}
}
cout<<ans;
return 0;
}
第二题-最多0的个数

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+100;
int n,m,arr[N];
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>arr[i];
arr[i]=abs(arr[i]);
}
sort(arr+1,arr+1+n);
int ans=0;
for(int i=1;i<=n;i++){
if(m>=arr[i]){
m-=arr[i];
ans++;
}else{
break;
}
}
cout<<ans;
return 0;
}
第三题-塔子哥的红黑树
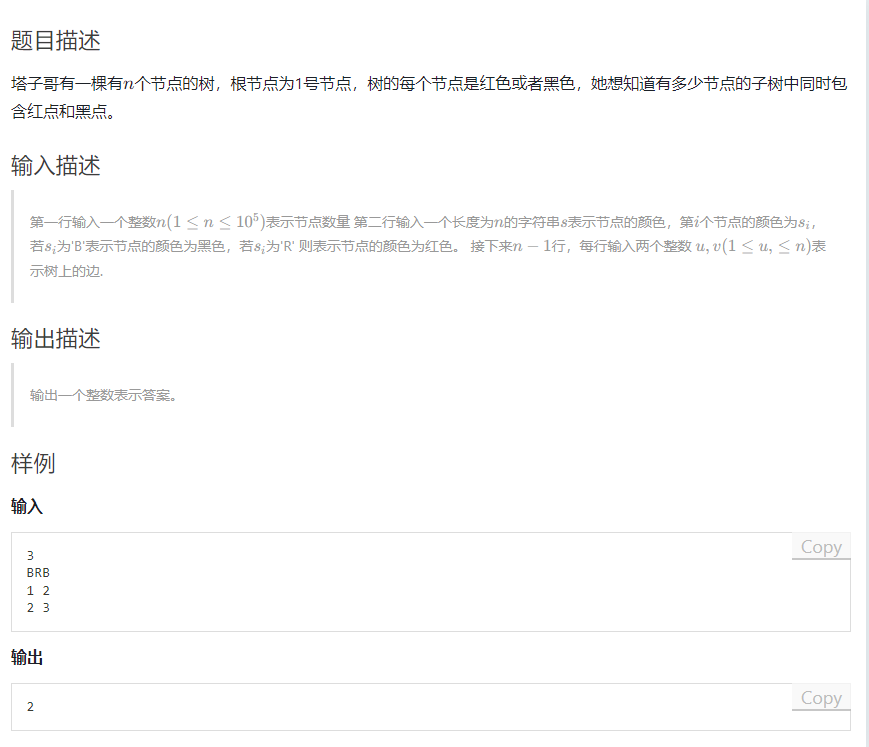
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+100;
int n,m,arr[N];
string s;
vector<int> g[N];
int ans=0;
pair<int,int> dfs(int u,int fa){
// cout<<u<<" "<<fa<<endl;
if(u==fa) return {};
int a=0,b=0;
if(s[u-1]=='R') a=1;
else b=1;
for(int i=0;i<g[u].size();i++){
int to=g[u][i];
if(to==fa) continue;
auto res=dfs(to,u);
a=a|res.first;
b=b|res.second;
}
if(a+b==2) ans++;
return {a,b};
}
signed main(){
cin>>n;
cin>>s;
for(int i=0;i<n-1;i++){
int a,b;
cin>>a>>b;
g[a].push_back(b);
g[b].push_back(a);
}
dfs(1,-1);
cout<<ans;
return 0;
}
第四题-塔子哥的因子数量

这个第四题有毒,思路一般,但是代码真的不好调试,今晚还把mod抄错了,1e9+7学成1e7+9,要不是眼睛看到了,这debug到明年~
说说思路吧,就是前缀和+二分,前缀保存质数的个数(2,3,5,7),二分分区间.还有mod的处理也是拉的一批。
代码很长也很挫QAq
#include<bits/stdc++.h>
using namespace std;
#define int unsigned long long
const int N = 2e5+100;
const int mod = 1e9+7;
struct ST{
int s2=0,s3=0,s5=0,s7=0;
}st[N],once[N];
int sum[N],sum1[N];
map<int,int> mp;
int n,m,q,u[N],v[N];
signed main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>u[i]>>v[i];
int s2=0,s3=0,s5=0,s7=0;
int tmp=u[i];
while(1){
if(tmp%2==0){
tmp=tmp/2;
s2++;
}else if(tmp%3==0){
tmp=tmp/3;
s3++;
}else if(tmp%5==0){
tmp=tmp/5;
s5++;
}else if(tmp%7==0){
tmp=tmp/7;
s7++;
}
if(tmp<=1) break;
}
st[i].s2=(st[i-1].s2+s2*v[i]%mod)%mod;
st[i].s3=(st[i-1].s3+s3*v[i]%mod)%mod;
st[i].s5=(st[i-1].s5+s5*v[i]%mod)%mod;
st[i].s7=(st[i-1].s7+s7*v[i]%mod)%mod;
sum[i]=sum[i-1]+v[i];
if(i==1) sum1[i]=1;
else sum1[i]=sum1[i-1]+v[i-1];
// 记录单个
once[i].s2=s2;
once[i].s3=s3;
once[i].s5=s5;
once[i].s7=s7;
}
// for(int i=1;i<=m;i++) cout<<sum[i]<<" ";cout<<endl;
cin>>q;
while(q--){
int ql,qr;
cin>>ql>>qr;
// 求取左端点
int pos1=1;
int l=1,r=m;
while(l<=r){
int mid=(l+r)/2;
if(sum1[mid]<=ql){
l=mid+1;
pos1=mid;
}else{
r=mid-1;
}
}
// 求取右端点
int pos2=m;
l=1,r=m;
while(l<=r){
int mid=(l+r)/2;
if(sum[mid]>=qr){
r=mid-1;
pos2=mid;
}else{
l=mid+1;
}
}
// cout<<"==debug:==\n"<<pos1<<" "<<pos2<<endl;
// cout<<sum[pos1]<<" "<<sum[pos2]<<endl;
int cur_s2=(st[pos2].s2-st[max(0ull,pos1-1)].s2+mod)%mod;
int cur_s3=(st[pos2].s3-st[max(0ull,pos1-1)].s3+mod)%mod;
int cur_s5=(st[pos2].s5-st[max(0ull,pos1-1)].s5+mod)%mod;
int cur_s7=(st[pos2].s7-st[max(0ull,pos1-1)].s7+mod)%mod;
// cout<<"begin:"<<cur_s2<<" "<<cur_s3<<" "<<cur_s5<<" "<<cur_s7<<endl;
// 处理前面多余的
cur_s2=(cur_s2-(ql-sum1[pos1])*once[pos1].s2%mod+mod)%mod;
cur_s3=(cur_s3-(ql-sum1[pos1])*once[pos1].s3%mod+mod)%mod;
cur_s5=(cur_s5-(ql-sum1[pos1])*once[pos1].s5%mod+mod)%mod;
cur_s7=(cur_s7-(ql-sum1[pos1])*once[pos1].s7%mod+mod)%mod;
// cout<<"process:"<<cur_s2<<" "<<cur_s3<<" "<<cur_s5<<" "<<cur_s7<<endl;
//处理后面多余的
cur_s2=(cur_s2-(sum[pos2]-qr)*once[pos2].s2%mod+mod)%mod;
cur_s3=(cur_s3-(sum[pos2]-qr)*once[pos2].s3%mod+mod)%mod;
cur_s5=(cur_s5-(sum[pos2]-qr)*once[pos2].s5%mod+mod)%mod;
cur_s7=(cur_s7-(sum[pos2]-qr)*once[pos2].s7%mod+mod)%mod;
// cout<<"last:"<<cur_s2<<" "<<cur_s3<<" "<<cur_s5<<" "<<cur_s7<<endl;
int ans=((((((cur_s2+1)*(cur_s3+1))%mod)*(cur_s5+1))%mod*(cur_s7+1))%mod);
cout<<ans<<endl;
}
return 0;
}
/*
8 4
1 2
2 1
3 3
4 2
10
2 5
7 8
1 1 2 3 3 3 4 4
1 2 3 4 5 6 7 8
*/
第五题-塔子哥的集合大小
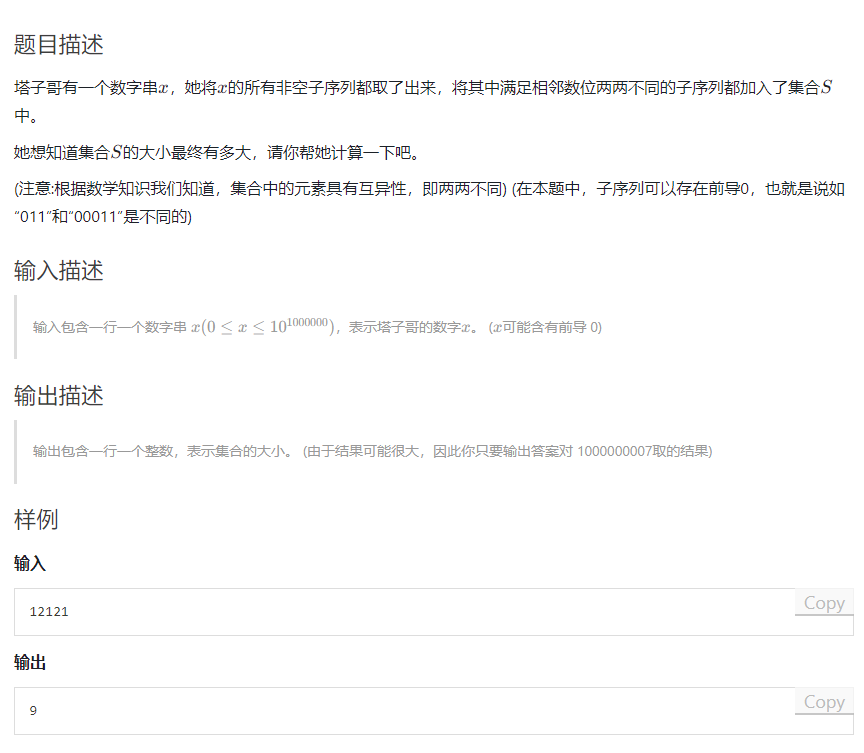
思路:DP
塔子哥题解
考虑dp,设f[i][c]表示前i个字符组成的以c为结尾的合法子序列个数。
假设当前位为j,由于要去重,前面所有以j结尾的子序列对于当前位来说同样可以构造,所以只需要考虑前一位不是以j结尾的答案,同时注意当前这一位可以单独放一个算子序列,所以加上1。
所以转移方程f[i][j] = sum(f[i]) - f[i - 1][j] + 1,最后统计sum(f[n - 1])即可。
由于dp转移只需要考虑前一位,所以可以优化空间复杂度为O(1)。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2E5+100;
const int mod = 1e9+7;
signed main(){
string s;
cin>>s;
int n=s.size();
vector<vector<int> >dp(n,vector<int>(10));// dp表示处理到第i位,并且以j数组结尾的子序列的个数
dp[0][s[0]-'0']=1;
for(int i=1;i<n;i++){
int sum=0;
int num=s[i]-'0';
for(int j=0;j<10;j++) sum=(sum+dp[i-1][j])%mod;
for(int j=0;j<10;j++){
if(j!=num){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=(sum-dp[i-1][j]+1+mod)%mod;
}
}
}
int ans=0;
for(int i=0;i<10;i++) ans=(ans+dp[n-1][i])%mod;
cout<<ans;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号