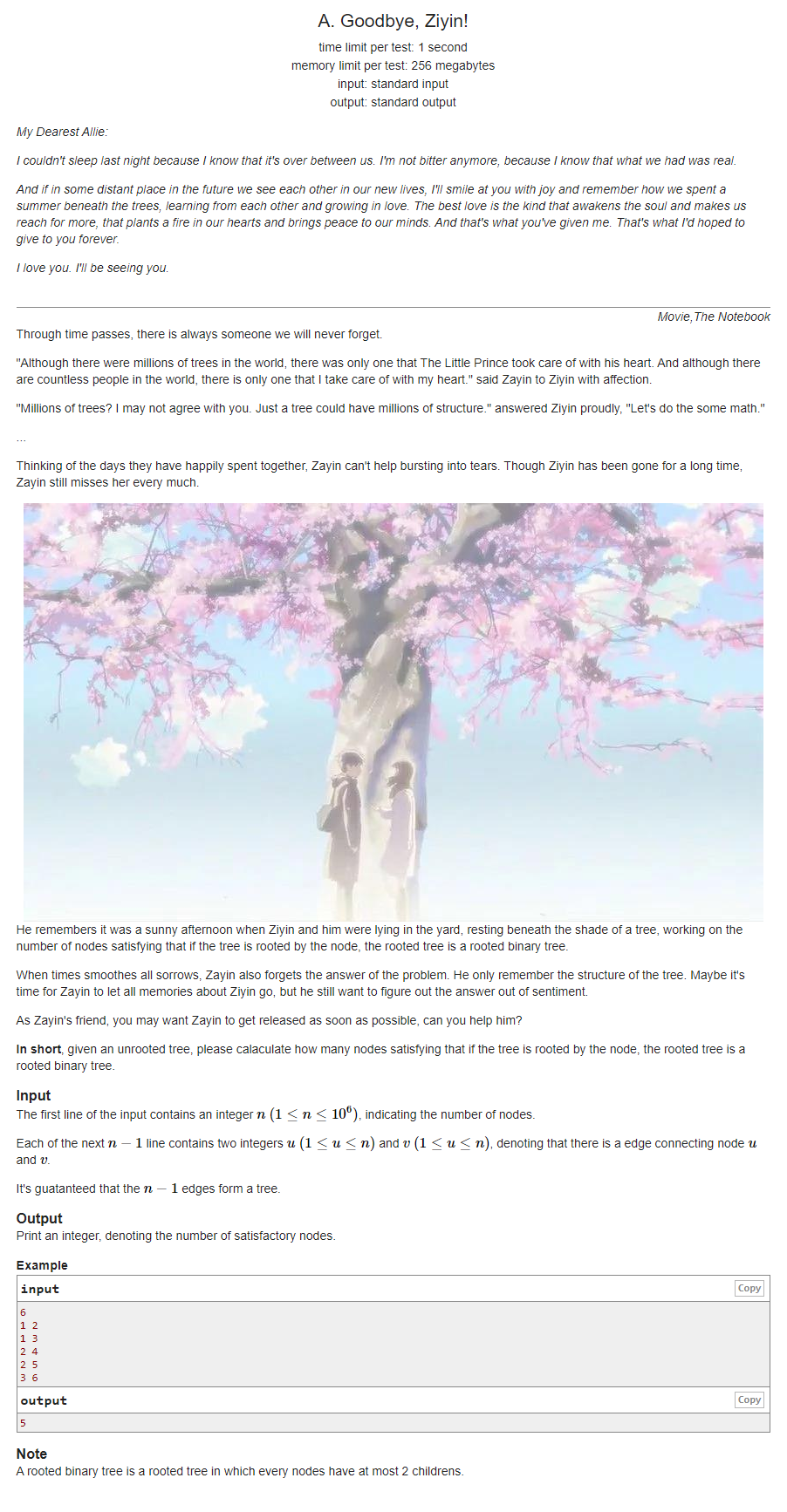
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 #define int long long
6 #define pb push_back
7
8 const int N=2e6+5,inf=0x3f3f3f3f;
9
10 int n,m;
11 int vis[N];
12 signed main(){
13 scanf("%lld",&n);
14 int mx=0;
15 for(int i=1;i<n;i++){
16 int x,y;
17 scanf("%lld%lld",&x,&y);
18 vis[x]++,vis[y]++;
19 mx=max(mx,max(vis[x],vis[y]));
20 }
21 if(mx>3){
22 cout<<"0";
23 return 0;
24 }
25 int s=0;
26 for(int i=1;i<=n;i++)
27 if(vis[i]==1||vis[i]==2) s++;
28 cout<<s;
29 return 0;
30 }
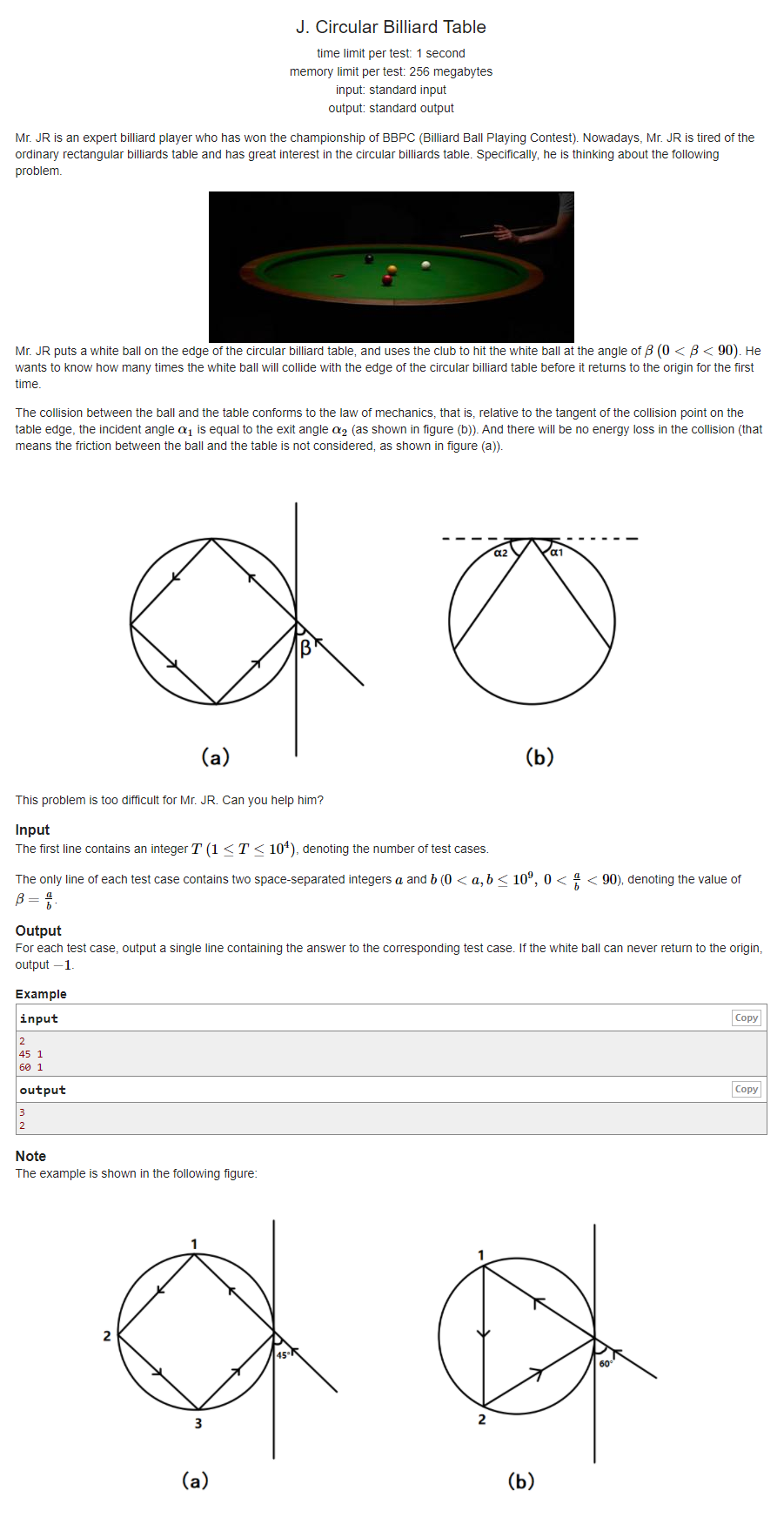
1 #include<bits/stdc++.h>
2 using namespace std;
3 #define int long long
4 #define N 666666
5
6 signed main(){
7 int T=1;
8 cin>>T;
9 while(T--){
10 int n,m;
11 cin>>n>>m;
12 cout<<((180*m)/__gcd(180*m,n))-1<<endl;
13 }
14
15
16
17 return 0;
18 }

认真审题,题目求的是不同本质的循环数。学一下Exkmp就会了。利用Z[数组]跑个后缀就🆗
1 #include<bits/stdc++.h>
2
3 using namespace std;
4
5 #define int long long
6 const int N = 3e6+100 ;
7 char str[N];
8 int Next[N];
9 int cur[N],ans[N];
10
11 void pre_EKMP(char x[],int m){
12 Next[0] = m;
13 int j = 0;
14 while( j+1 < m && x[j] == x[j+1] )j++;
15 Next[1] = j;
16 int k = 1;
17 for(int i = 2; i < m; i++){
18 int p = Next[k]+k-1;
19 int L = Next[i-k];
20 if( i+L < p+1 ) Next[i] = L;
21 else{
22 j = max(0ll,p-i+1);
23 while( i+j < m && x[i+j] == x[j])j++;
24 Next[i] = j;
25 k = i;
26 }
27 }
28 }
29 signed main(){
30 cin>>str;
31 int n=strlen(str);
32 pre_EKMP(str,n);
33 for(int i=n-1;i>0;i--){
34 cur[i]=cur[i+1];
35 int len=n-i;
36 if(len==Next[i]){
37 cur[i]=cur[i+1]+1;
38 }
39 }
40 ans[0]=0;
41 for(int i=1;i<n;i++){
42 int t=min(i,n-i-1);
43 ans[i]=cur[n-t];
44 }
45 ans[n-1]=0;
46 int Q=1;
47 cin>>Q;
48 while(Q--){
49 int x;
50 scanf("%lld",&x);
51 printf("%lld\n",ans[x-1]);
52 }
53 return 0;
54 }
55

题目不难,只要分析好时间复杂度就行。还有,你需要一个好板子!
1 #include <iostream>
2 #include <cstdio>
3 #include <algorithm>
4 #include <queue>
5 #include <string>
6 using namespace std;
7 #define int long long
8 const int N = 5e4+10 , M = 1e5+100;
9 const int mod=998244353;
10 int h,w,a,b;
11 int fac[N],fnv[N];
12 int ans;
13 int quickmod(int x,int y)
14 {
15 int ans=1;
16 for(;y;y>>=1)
17 {
18 if(y&1) ans=ans*x%mod;
19 x=x*x%mod;
20 }
21 return ans;
22 }
23
24 void build()
25 {
26 fac[0]=1;
27 for(int i=1;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod;
28 fnv[N-1]=quickmod(fac[N-1],mod-2);
29 for(int i=N-2;i>=0;i--) fnv[i]=1ll*fnv[i+1]*(i+1)%mod;
30 }
31
32 int C(int x,int y)
33 {
34 if(x<y) return 0;
35 return 1ll*fac[x]*fnv[y]%mod*fnv[x-y]%mod;
36 }
37 int n,m;
38 int p[M],arr[M],mp[M],cnt;
39 signed main(){
40 build();
41 scanf("%lld%lld",&n,&m);
42 int mx=0;
43 for(int i=1;i<=n;i++){
44 scanf("%lld",&arr[i]);
45 if(arr[i]!=0){
46 if(!mp[arr[i]]){
47 p[++cnt]=arr[i];
48 }
49 mp[arr[i]]++;
50 }
51 mx=max(mx,arr[i]);
52 }
53 for(int i=1;i<=m;i++){
54 if(i<mx){
55 printf("0\n");
56 continue;
57 }
58 int cur=1;
59 for(int j=1;j<=cnt;j++){
60 int x=p[j];
61 int num=mp[x];
62 cur=(cur*quickmod(C(i,x),num))%mod;
63 }
64 printf("%lld\n",cur);
65 }
66 return 0;
67 }








