AtCoder Beginner Contest 216【C：简单思维】【D：双端队列+BFS 模拟】【E：优先队列+map 数学】【F：背包问题+优化】

 

 

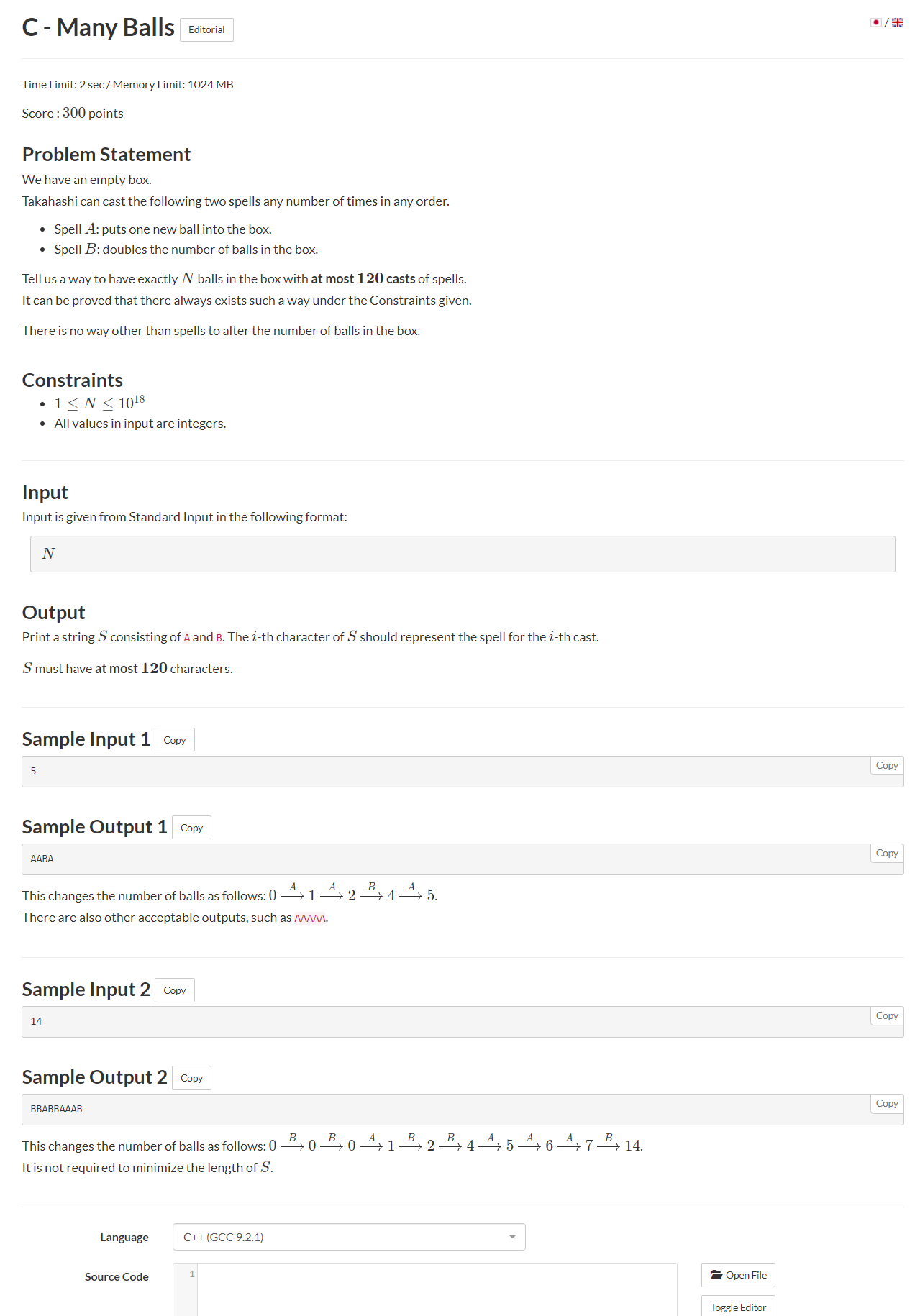
#include<bits/stdc++.h>

using namespace std;
#define int  long long
#define pb push_back

int n;
vector<int> v;
signed main(){
    cin>>n; 
    while(n){
        if(n%2==0)    
            v.pb(1),n/=2;
        else
            v.pb(0),n--;
    }
    for(int i=v.size()-1;i>=0;i--)
        if(!v[i]) cout<<"A";else cout<<"B";
    
    return 0;
}
/*
5
0 1 2 4
*/

 

 

想了想，感觉没什么思维。直接用队列模拟就行

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int N = 5e5 + 100 ;

deque<int> q[N];
queue<int> p;
int n,m,k;
vector<int> id[N];
signed main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>k;
        for(int j=1;j<=k;j++){
            int x;
            cin>>x;
            q[i].push_back(x);
        }
    }
    for(int i=1;i<=m;i++){
        if(q[i].size()<=0){
            continue;
        }
        id[q[i].front()].push_back(i);
        if(id[q[i].front()].size()<=1){
            continue;
        }else{
            p.push(q[i].front());
            while(!p.empty()){
                int tot=p.front();
                p.pop();
                if(id[tot].size()==2){
                    int idx=id[tot][0];
                    q[idx].pop_front();
                    if(q[idx].size()>0){
                        id[q[idx].front()].push_back(idx);
                        p.push(q[idx].front());                        
                    }
                    idx=id[tot][1];
                    q[idx].pop_front();
                    if(q[idx].size()>0){
                        id[q[idx].front()].push_back(idx);
                        p.push(q[idx].front());                        
                    }
                    id[tot].clear();
                }
            }
        }
    }    
    int F=1;
    for(int i=1;i<=m;i++){
        if(q[i].size()){
            F=0;
            break;
        }
    }
    if(F) cout<<"Yes";else cout<<"No";
    return 0;
}

 

 

 

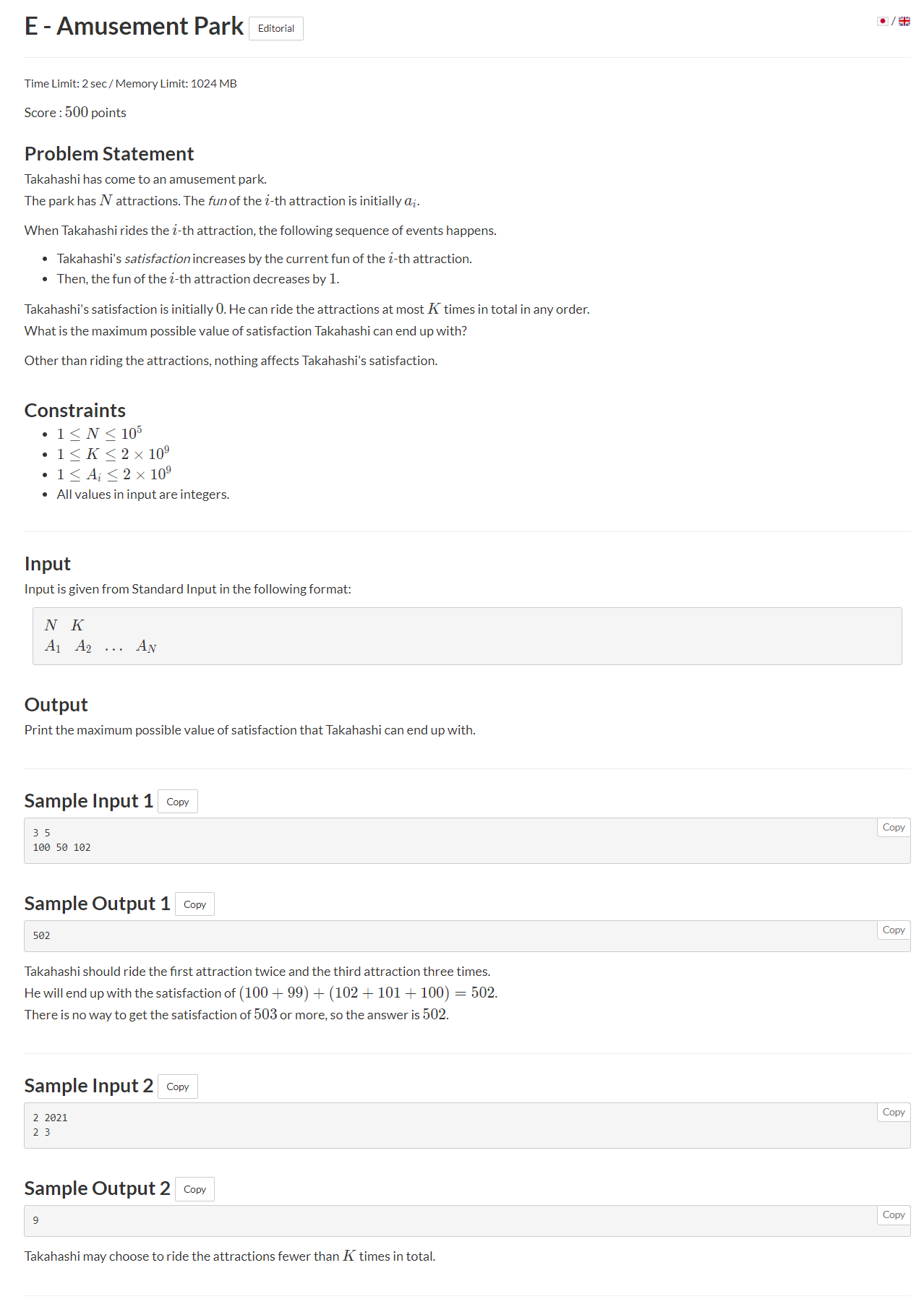
思路：优先队列模拟即可。剩下得就交给数学啦

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e5 + 100 ;
int arr[N],n,k;
map<int,int> mp;
priority_queue<int> q;
signed main(){
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>arr[i];
        if(mp[arr[i]]){
            mp[arr[i]]++;
        }else{
            q.push(arr[i]);
            mp[arr[i]]++;
        }
    }
    int ans=0;
    while(q.size()){
        int num=q.top();
        q.pop();
        if(q.size()){
            int tmp=q.top();
            int sum=(num-tmp)*mp[num];
            if(sum<=k){
                ans+=((((num+tmp+1))*(num-tmp))/2)*(mp[num]);
//                cout<<"1 "<<ans<<" "<<sum<<endl;
                mp[tmp]=mp[tmp]+mp[num];
                mp[num]=0;
                k-=sum;
            }else{
                
                ans+=(((num+(num-(k/mp[num]-1)))*(k/mp[num]))/2)*mp[num]+(num-k/mp[num])*(k%mp[num]);
//                cout<<"2 "<<ans<<endl;
                break;
            }
        }else{
            if(mp[num]*num<=k){
                ans+=mp[num]*(num*(num+1)/2);
                
//                cout<<"3 "<<ans<<endl;
            }else{
                ans+=(((num+(num-(k/mp[num]-1)))*(k/mp[num]))/2)*mp[num]+(num-k/mp[num])*(k%mp[num]);
                break;
//                cout<<"4 "<<ans<<endl;
            }
            
        }
    }
    cout<<ans<<endl; 
    return 0;
}
/*

*/

 

 

 

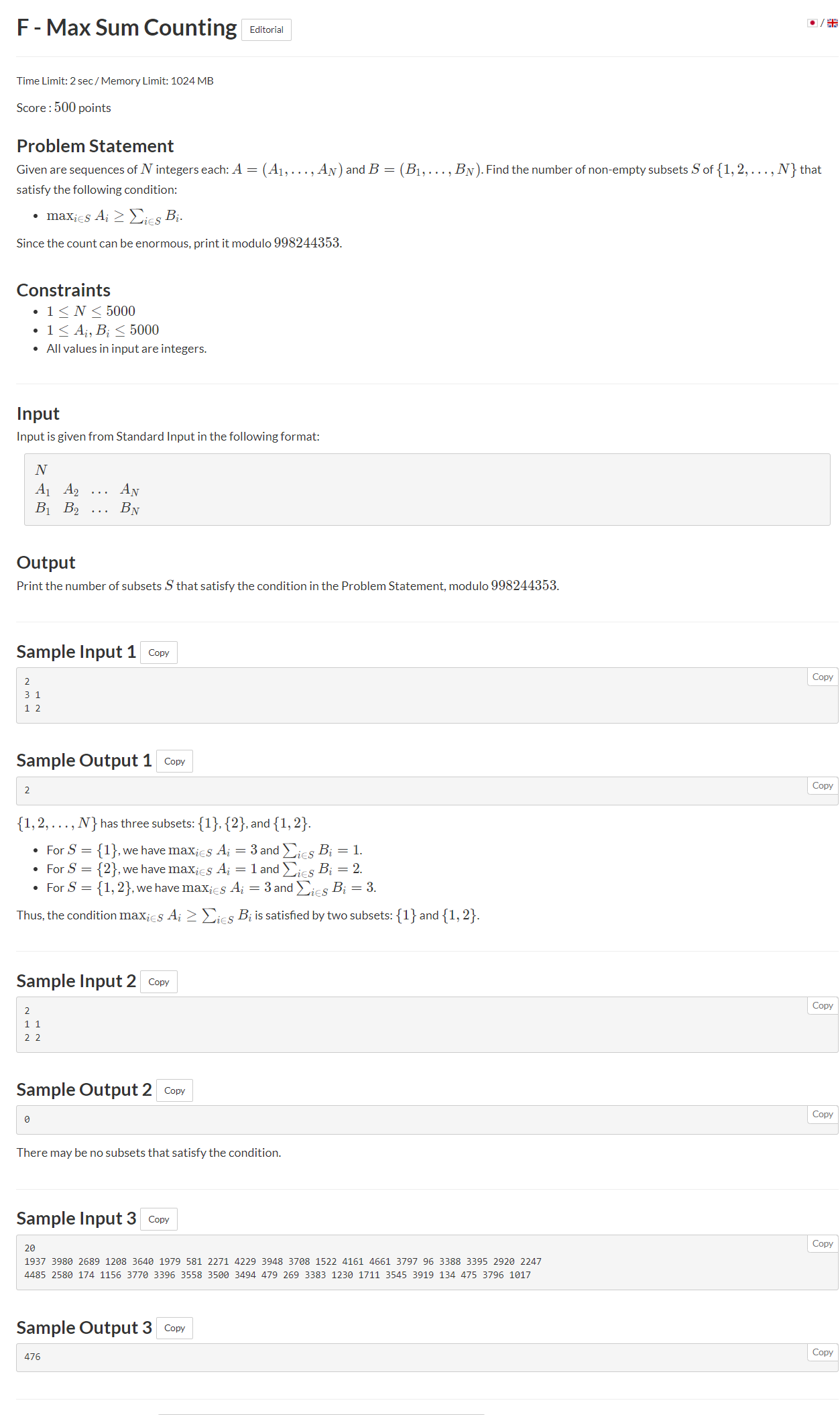
题意：给你n物品，每个物品有a和b两个属性。你现在要挑选出一个集合S。
使得max ai >= sum(bi)  {i ∈ S} 问有多少种挑选方案。S不为空

思路：
将Ai排序，可以先将每个Ai想象成一个体积为Ai的背包，找前i个Bi能放下的数量。
接着我们考虑背包DP方程：DP[i][j]:表示当前已经处理到第i为，且第Bi为必拿，那么J=A[i]-B[i],J为体积。这样的话就可以写出一个O（N^3）的算法。但是过不了QAQ我们要进行优化，化到O（N^2）
学习一下优化:我们将J从原先不小于（A[i]-B[i]）扩展为5000，向后优化。(秒啊！！）这样就能直接统计！

O（N^3）

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int N = 6e3+100 , mod = 998244353;
struct str{
    int a,b;
}st[N];
bool cmp(str A,str B){
    if(A.a!=B.a){
        return A.a<B.a;
    }else{
        return A.b<B.b;
    }
}
int qpow(int a,int b){
    int s=1;
    while(b){
        if(b%2){
            s=(s*a)%mod;
        }
        a=(a*a)%mod;
        b/=2;
    }
    return s; 
}
int dp[N];
int n;
int w[N]; 
//
signed main(){
    int ans=0;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>st[i].a;
    for(int i=1;i<=n;i++) cin>>st[i].b;
    sort(st+1,st+1+n,cmp);
    for(int i=1;i<=n;i++){
        int val=st[i].a-st[i].b;
            
        memset(dp,0,sizeof(dp));
        dp[0]=1;
        for(int j=1;j<i;j++){
            for(int k=val;k>=st[j].b;k--){
                dp[k]=(dp[k]+dp[k-st[j].b])%mod;                
            }
        }
        for(int j=0;j<=val;j++) 
            ans=(ans+dp[j])%mod;
    }
    cout<<ans;
    return 0;
}

O(N^2)

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int N = 6e3+100 , mod = 998244353;
struct str{
    int a,b;
}st[N];
bool cmp(str A,str B){
    if(A.a!=B.a){
        return A.a<B.a;
    }else{
        return A.b<B.b;
    }
}
int qpow(int a,int b){
    int s=1;
    while(b){
        if(b%2){
            s=(s*a)%mod;
        }
        a=(a*a)%mod;
        b/=2;
    }
    return s; 
}
int dp[N];
int n;
int w[N]; 
signed main(){
    int ans=0;
    cin>>n;
    
    for(int i=1;i<=n;i++) cin>>st[i].a;
    for(int i=1;i<=n;i++) cin>>st[i].b;
    sort(st+1,st+1+n,cmp);
    dp[0]=1;
    for(int i=1;i<=n;i++){
        int val=st[i].a-st[i].b;
        for(int j=0;j<=val;j++) 
            ans=(ans+dp[j])%mod;        
        for(int j=5100;j>=st[i].b;j--){
            dp[j]=(dp[j]+dp[j-st[i].b])%mod;                
        }
    }
    cout<<ans;
    return 0;
}