数学基础(一)
原文链接:http://www.one2know.cn/shuxuejichu1/
函数
- 函数
给数集A一个法则/映射f,得到另一个数集B,记为B=f(A) - 反函数
x,y一一对应才有反函数,与原函数关于y=x对称
反函数一定是单调的,而且单调性与原函数相同 - 复合函数
(f 。g)(x) = f[g(x)] - 基本初等函数
1)幂函数 2)指数函数 3)对数函数 4)三角函数(sin,cos,tan,cot,sec,csc)
5)反三角函数(arcsin,arccos,arctanarccot)
极限
- 数列极限
对f(x),有常数a,对任意无论多小的δ,总存在正数X,使x>X时,|f(x)-a|<δ恒成立 - 函数极限
1)x0 2)x0+ 3)x0- 4)∞ 5)+∞ 6)-∞ - 函数极限性质
1)唯一性 2)局部有限性 - 两个准则
1)夹逼准则 - 重要极限
1)lim(x➡0)sinx/x=1 2)lim(x➡∞)(1+1/x)^x=e
导数
- 导数
![]()
- 常用导数
![]()
- 导数法则
![]()
- 反函数求导
![]()
- 复合函数求导
![]()
- 高阶导数
![]()
- 导数的应用
1)函数单调性
凹凸性:二阶导>0:凹,二阶导数<0:凸
![]()
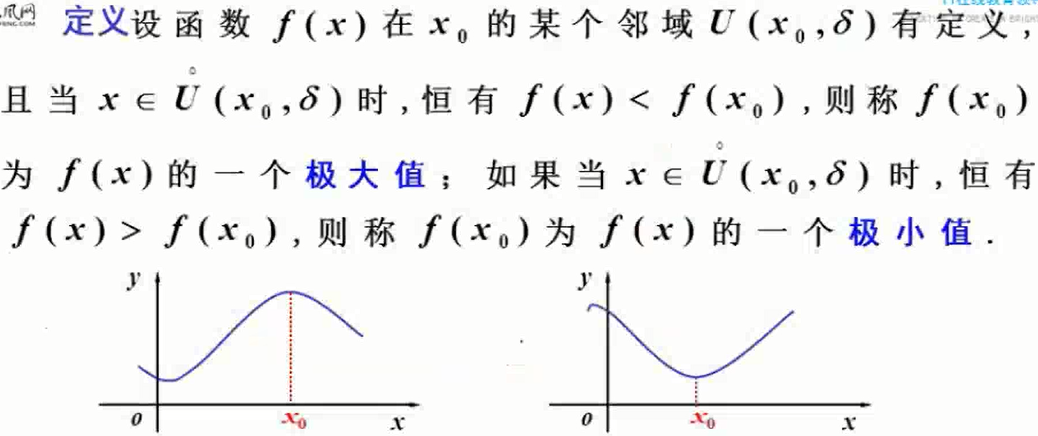
2)函数极值与最值
![]()
3)泰勒公式
![]()
多元函数
- 二元函数
每个点(x,y)∈平面D,有对应的法则得到z,记为z=f(x,y) - 多元函数:多维
- 多元函数极限
![]()
- 多元函数偏导
- 高阶偏导数
向量
- 向量,向量的模,单位向量,向量的运算
- 方向导数
![]()
对于二元函数
![]()
- 梯度:下降最快方向,各方向偏导向量相加
- 矩阵,矩阵运算,转置
- 方阵行列式:
|A|或det(A) - 代数余子式:
Aij = (-1)^(i+j)Mij
det(A)=某一行或某一列元素与其代数余子式的乘积和 - 伴随矩阵:由代数余子式代替对应元素构成的矩阵
- 方阵的逆:A,存在B使 AB=BA=E,称A与B互为逆矩阵
可逆矩阵 = 非奇异矩阵
判定可逆: 可逆矩阵的行列式 ≠ 0
运算:
![]()
- 矩阵的初等行变换
目的: 化简矩阵,化成阶梯型
1)对调两行 2)对第i行乘不为0的数 3)第i行的k倍加到第j行
A经过有限次的初等变换➡B,即A与B等价,记为 A~B,等价的线性方程同解
等价的性质:
1)自反性:A~A 2)对称性:若AB,则BA 3)传递性:若AB,且BC,则A~C
初等行列变换➡最简矩阵(标准形),能看出几阶,即秩 - 初等行变换求逆
( A , E ) = ( E , A^-1 ) - 矩阵线性表示
![]()
- 对称矩阵: A = A的转置
- 线性方程组的解
![]()
![]()
![]()
特征值 特征向量
- 概念:A为n阶矩阵,若数λ和n维非零列向量满足
Ax=λx,那么数λ称为A的特征值,x称为A的对应于特征值λ的特征向量,并且|λE-A|叫做A的特征多项式 - 求法:解
|λE-A| = 0,解出λ,然后解|λE-A|*x = 0
![]()


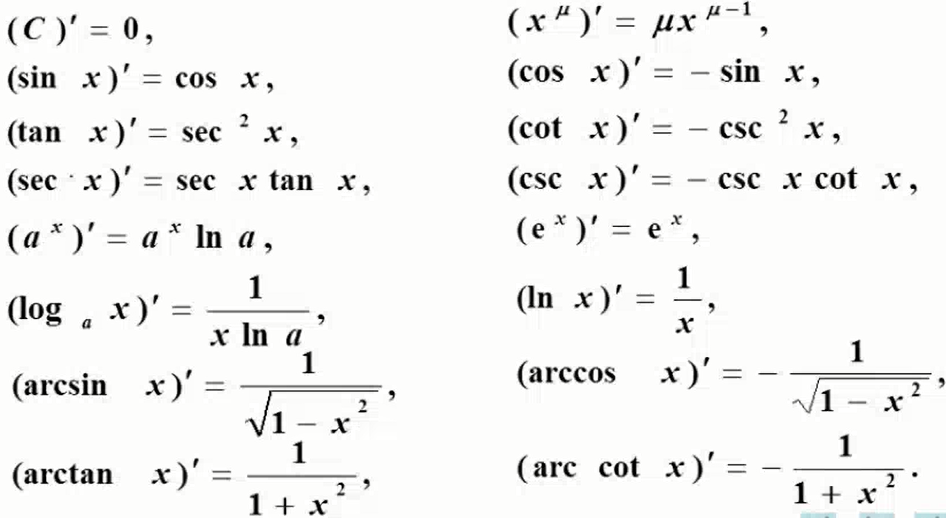

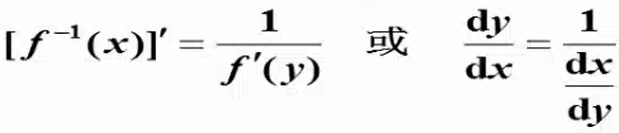



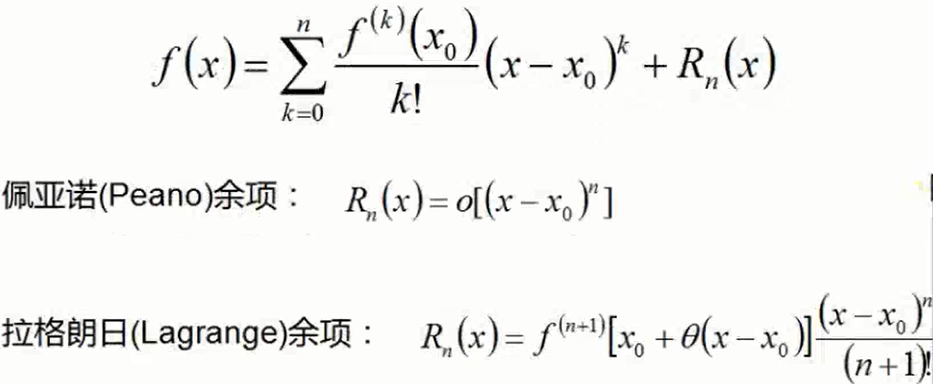



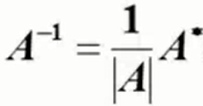
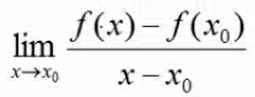



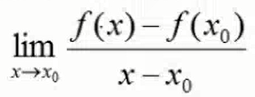

 浙公网安备 33010602011771号
浙公网安备 33010602011771号