Data Structure and Algorithm - Day 07
-
Division
find sub-problems, split and merge
def divide_conquer(problem, param1, param2, ...): # recursion terminator if problem is None: print_result return # prepare data data = prepare_data(problem) subproblems = split_problem(problem, data) # conquer subproblems subresult1 = self.divide_conquer(subproblems[0], p1, p2, ...) subresult2 = self.divide_conquer(subproblems[1], p1, p2, ...) subresult3 = self.divide_conquer(subproblems[2], p1, p2, ...) ... # process and generate the final result result = process_result(subresult1, subresult2, subresult3, ...) # revert the current level states -
BackTracking
-
50. Pow(x, n)
Implement pow(x, n), which calculates x raised to the power n (i.e. xn).
Example 1:
Input: x = 2.00000, n = 10 Output: 1024.00000Example 2:
Input: x = 2.10000, n = 3 Output: 9.26100Example 3:
Input: x = 2.00000, n = -2 Output: 0.25000 Explanation: 2-2 = 1/22 = 1/4 = 0.25Constraints:
-100.0 < x < 100.0-231 <= n <= 231-1-104 <= xn <= 104
class Solution { public double myPow(double x, int n) { if (x == 0 || x == 1) return x; if (n == 0) return 1; long n1 = n; if (n1 < 0) { x = 1 / x; n1 = -n1; } return divide(x, n1); } private double divide(double x, long n) { if (n == 1) return x; double subresult = divide(x, n/2); return subresult * subresult * (n%2 == 0 ? 1 : x); } } -
78. Subsets
Given an integer array
numsof unique elements, return all possible subsets (the power set).The solution set must not contain duplicate subsets. Return the solution in any order.
Example 1:
Input: nums = [1,2,3] Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]Example 2:
Input: nums = [0] Output: [[],[0]]Constraints:
1 <= nums.length <= 10-10 <= nums[i] <= 10- All the numbers of
numsare unique.
class Solution { public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> res = new ArrayList<>(); List<Integer> list = new ArrayList<>(); dfs(res, list, nums, 0); return res; } private void dfs(List<List<Integer>> res, List<Integer> list, int[] nums, int number) { if (number == nums.length) { res.add(new ArrayList<>(list)); return ; } // branch1 dfs(res, list, nums, number + 1); // branch2 list.add(nums[number]); dfs(res, list, nums, number + 1); list.remove(list.size() - 1); } }class Solution { public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> res = new ArrayList<>(); res.add(new ArrayList<>()); for (int i = 0; i < nums.length; i++) { for (int j = 0; j < (int)Math.pow(2, i); j++) { List<Integer> list = new ArrayList<>(res.get(j)); list.add(nums[i]); res.add(list); } } return res; } } -
169. Majority Element
Given an array
numsof sizen, return the majority element.The majority element is the element that appears more than
⌊n / 2⌋times. You may assume that the majority element always exists in the array.Example 1:
Input: nums = [3,2,3] Output: 3Example 2:
Input: nums = [2,2,1,1,1,2,2] Output: 2Constraints:
n == nums.length1 <= n <= 5 * 104-231 <= nums[i] <= 231 - 1
class Solution { public int majorityElement(int[] nums) { int res = nums[0], quantity = 1; for (int i = 1; i < nums.length; i++) { if (nums[i] == res) quantity++; else if (quantity > 0) quantity--; else { res = nums[i]; quantity = 1; } } return res; } }class Solution { public int majorityElement(int[] nums) { Arrays.sort(nums); return nums[nums.length / 2]; } }// divise for division class Solution { private int countInRange(int[] nums, int num, int lo, int hi) { int count = 0; for (int i = lo; i <= hi; i++) { if (nums[i] == num) { count++; } } return count; } private int majorityElementRec(int[] nums, int lo, int hi) { // base case; // the only element in an array of size 1 is the majority element. if (lo == hi) { return nums[lo]; } // recurse on left and right halves of this slice. int mid = (hi - lo) / 2 + lo; int left = majorityElementRec(nums, lo, mid); int right = majorityElementRec(nums, mid + 1, hi); // if the two halves agree on the majority element, return it. if (left == right) { return left; } // otherwise, count each element and return the "winner". int leftCount = countInRange(nums, left, lo, hi); int rightCount = countInRange(nums, right, lo, hi); return leftCount > rightCount ? left : right; } public int majorityElement(int[] nums) { return majorityElementRec(nums, 0, nums.length - 1); } } -
17. Letter Combinations of a Phone Number
Given a string containing digits from
2-9inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
![img]()
Example 1:
Input: digits = "23" Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]Example 2:
Input: digits = "" Output: []Example 3:
Input: digits = "2" Output: ["a","b","c"]Constraints:
0 <= digits.length <= 4digits[i]is a digit in the range['2', '9'].
class Solution { String[] letters = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}; public List<String> letterCombinations(String digits) { List<String> res = new ArrayList<>(); if (digits == null || digits.length() == 0) return res; StringBuilder sb = new StringBuilder(); dfs(res, sb, digits, 0); return res; } private void dfs(List<String> res, StringBuilder sb, String digits, int index) { if (index == digits.length()) { res.add(String.valueOf(sb)); return ; } for (char ch : letters[digits.charAt(index) - '0'].toCharArray()) { sb.append(ch); dfs(res, sb, digits, index + 1); sb.deleteCharAt(sb.length() - 1); } } } -
51. N-Queens
The n-queens puzzle is the problem of placing
nqueens on ann x nchessboard such that no two queens attack each other.Given an integer
n, return all distinct solutions to the n-queens puzzle.Each solution contains a distinct board configuration of the n-queens' placement, where
'Q'and'.'both indicate a queen and an empty space, respectively.Example 1:
![img]()
Input: n = 4 Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] Explanation: There exist two distinct solutions to the 4-queens puzzle as shown aboveExample 2:
Input: n = 1 Output: [["Q"]]Constraints:
1 <= n <= 9
class Solution { public List<List<String>> solveNQueens(int n) { List<List<String>> res = new ArrayList<>(); char[][] board = new char[n][n]; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { board[i][j] = '.'; } } Set[] sets = new Set[3]; // |:j, \:j-i, /:i+j for (int i = 0; i < 3; i++) { sets[i] = new HashSet<>(); } dfs(res, board,0, n, sets); return res; } private void dfs(List<List<String>> res, char[][] board, int i, int n, Set[] sets) { if (i == n) { List<String> list = new ArrayList<>(); for (char[] chs : board) { list.add(String.valueOf(chs)); } res.add(list); return ; } for (int j = 0; j < n; j++) { if (sets[0].contains(j) || sets[1].contains(j-i) || sets[2].contains(i+j)) { continue; } board[i][j] = 'Q'; sets[0].add(j); sets[1].add(j-i); sets[2].add(i+j); dfs(res, board, i + 1, n, sets); board[i][j] = '.'; sets[0].remove(j); sets[1].remove(j-i); sets[2].remove(i+j); } } } -
dfs & bfs
ergodic: every node lookup once
# dfs - recursion def dfs(node): if node in visited: # already visited return visited.add(node) # process current logic for next_node in node.nexts: dfs(next_node) # dfs - not recursion, use stack def dfs(root): if root is None: return [] visited, stack = [], [root] while stack: node = stack.pop() visited.add(node) # process current node for next_node in node.nexts: stack.push(next_node) # other processing work# bfs - use queue def bfs(graph, start, end): queue = [] queue.append(start) visited.add(start) while queue: node = queue.pop() visited.add(node) process(node) for next_node in node.nexts: queue.push(next_node) # other processing work -
102. Binary Tree Level Order Traversal
Given the
rootof a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).Example 1:
![img]()
Input: root = [3,9,20,null,null,15,7] Output: [[3],[9,20],[15,7]]Example 2:
Input: root = [1] Output: [[1]]Example 3:
Input: root = [] Output: []Constraints:
- The number of nodes in the tree is in the range
[0, 2000]. -1000 <= Node.val <= 1000
// bfs - 1ms class Solution { public List<List<Integer>> levelOrder(TreeNode root) { List<List<Integer>> res = new ArrayList<>(); if (root == null) return res; Deque<TreeNode> queue = new LinkedList<>(); queue.addLast(root); while (!queue.isEmpty()) { int size = queue.size(); List<Integer> list = new LinkedList<>(); while (size-- > 0) { TreeNode node = queue.pollFirst(); list.add(node.val); if (node.left != null) queue.addLast(node.left); if (node.right != null) queue.addLast(node.right); } res.add(list); } return res; } } // dfs - 0ms class Solution { public List<List<Integer>> levelOrder(TreeNode root) { List<List<Integer>> res = new ArrayList<>(); if (root == null) return res; dfs(res, root, 1); return res; } private void dfs(List<List<Integer>> res, TreeNode root, int deep) { if (root == null) return ; if (deep > res.size()) { res.add(new ArrayList<>()); } res.get(deep - 1).add(root.val); dfs(res, root.left, deep + 1); dfs(res, root.right, deep + 1); } } - The number of nodes in the tree is in the range
-
433. Minimum Genetic Mutation
A gene string can be represented by an 8-character long string, with choices from
"A","C","G","T".Suppose we need to investigate about a mutation (mutation from "start" to "end"), where ONE mutation is defined as ONE single character changed in the gene string.
For example,
"AACCGGTT"->"AACCGGTA"is 1 mutation.Also, there is a given gene "bank", which records all the valid gene mutations. A gene must be in the bank to make it a valid gene string.
Now, given 3 things - start, end, bank, your task is to determine what is the minimum number of mutations needed to mutate from "start" to "end". If there is no such a mutation, return -1.
Note:
- Starting point is assumed to be valid, so it might not be included in the bank.
- If multiple mutations are needed, all mutations during in the sequence must be valid.
- You may assume start and end string is not the same.
Example 1:
start: "AACCGGTT" end: "AACCGGTA" bank: ["AACCGGTA"] return: 1Example 2:
start: "AACCGGTT" end: "AAACGGTA" bank: ["AACCGGTA", "AACCGCTA", "AAACGGTA"] return: 2Example 3:
start: "AAAAACCC" end: "AACCCCCC" bank: ["AAAACCCC", "AAACCCCC", "AACCCCCC"] return: 3class Solution { public int minMutation(String start, String end, String[] bank) { int n = bank.length; boolean[] visited = new boolean[n]; int res = 0; Deque<String> queue = new LinkedList<>(); queue.addLast(start); while (!queue.isEmpty()) { int size = queue.size(); res++; while (size-- > 0) { String s = queue.pollFirst(); for (int i = 0; i < n; i++) { if (visited[i]) continue; if (can(s, bank[i])) { if (bank[i].equals(end)) return res; queue.addLast(bank[i]); visited[i] = true; } } } } return -1; } private boolean can(String s, String t) { boolean flag = false; for (int i = 0; i < 8; i++) { if (s.charAt(i) != t.charAt(i)) { if (flag) return false; flag = true; } } return true; } } -
515. Find Largest Value in Each Tree Row
Given the
rootof a binary tree, return an array of the largest value in each row of the tree (0-indexed).Example 1:
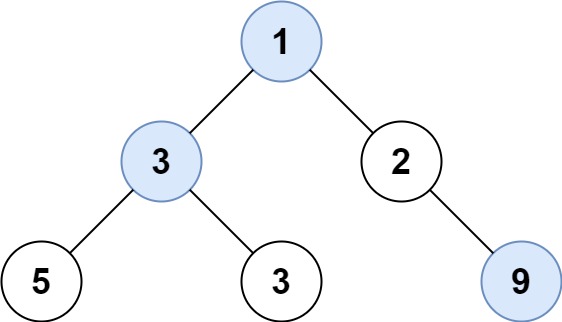
![img]()
Input: root = [1,3,2,5,3,null,9] Output: [1,3,9]Example 2:
Input: root = [1,2,3] Output: [1,3]Example 3:
Input: root = [1] Output: [1]Example 4:
Input: root = [1,null,2] Output: [1,2]Example 5:
Input: root = [] Output: []Constraints:
- The number of nodes in the tree will be in the range
[0, 104]. -231 <= Node.val <= 231 - 1
class Solution { public List<Integer> largestValues(TreeNode root) { List<Integer> res = new ArrayList<>(); bfs(res, root, 1); return res; } private void bfs(List<Integer> res, TreeNode root, int deep) { if (root == null) return ; if (deep > res.size()) { res.add(root.val); } else { res.set(deep - 1, Math.max(res.get(deep - 1), root.val)); } bfs(res, root.left, deep + 1); bfs(res, root.right, deep + 1); } } - The number of nodes in the tree will be in the range
-
46. Permutations
Given an array
numsof distinct integers, return all the possible permutations. You can return the answer in any order.Example 1:
Input: nums = [1,2,3] Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]Example 2:
Input: nums = [0,1] Output: [[0,1],[1,0]]Example 3:
Input: nums = [1] Output: [[1]]Constraints:
1 <= nums.length <= 6-10 <= nums[i] <= 10- All the integers of
numsare unique.
class Solution { public List<List<Integer>> permute(int[] nums) { List<List<Integer>> res = new ArrayList<>(); int n = nums.length; boolean[] visited = new boolean[n]; List<Integer> list = new ArrayList<>(); dfs(nums, res, list, visited, n); return res; } private void dfs(int[] nums, List<List<Integer>> res, List<Integer> list, boolean[] visited, int n) { int size = list.size(); if (size == n) { res.add(new ArrayList<>(list)); return ; } for (int i = 0; i < n; i++) { if (visited[i]) continue; list.add(nums[i]); visited[i] = true; dfs(nums, res, list, visited, n); visited[i] = false; list.remove(size); } } }






 浙公网安备 33010602011771号
浙公网安备 33010602011771号