Data Structure and Algorithm - Day 12

• Advanced Search

  • Pruning

  • Bidirectional Breadth First Search

  • Heuristic search (A* Search)

    public class AStar
    {
        public final static int BAR = 1; // 障碍值
        public final static int PATH = 2; // 路径
        public final static int DIRECT_VALUE = 10; // 横竖移动代价
        public final static int OBLIQUE_VALUE = 14; // 斜移动代价
    
        Queue<Node> openList = new PriorityQueue<Node>(); // 优先队列(升序)
        List<Node> closeList = new ArrayList<Node>();
    
        /**
         * 开始算法
         */
        public void start(MapInfo mapInfo)
        {
            if(mapInfo==null) return;
            // clean
            openList.clear();
            closeList.clear();
            // 开始搜索
            openList.add(mapInfo.start);
            moveNodes(mapInfo);
        }
    
        /**
         * 移动当前结点
         */
        private void moveNodes(MapInfo mapInfo)
        {
            while (!openList.isEmpty())
            {
                Node current = openList.poll();
                closeList.add(current);
                addNeighborNodeInOpen(mapInfo,current);
                if (isCoordInClose(mapInfo.end.coord))
                {
                    drawPath(mapInfo.maps, mapInfo.end);
                    break;
                }
            }
        }
    
        /**
         * 在二维数组中绘制路径
         */
        private void drawPath(int[][] maps, Node end)
        {
            if(end==null||maps==null) return;
            System.out.println("总代价：" + end.G);
            while (end != null)
            {
                Coord c = end.coord;
                maps[c.y][c.x] = PATH;
                end = end.parent;
            }
        }
    
        /**
         * 添加所有邻结点到open表
         */
        private void addNeighborNodeInOpen(MapInfo mapInfo,Node current)
        {
            int x = current.coord.x;
            int y = current.coord.y;
            // 左
            addNeighborNodeInOpen(mapInfo,current, x - 1, y, DIRECT_VALUE);
            // 上
            addNeighborNodeInOpen(mapInfo,current, x, y - 1, DIRECT_VALUE);
            // 右
            addNeighborNodeInOpen(mapInfo,current, x + 1, y, DIRECT_VALUE);
            // 下
            addNeighborNodeInOpen(mapInfo,current, x, y + 1, DIRECT_VALUE);
            // 左上
            addNeighborNodeInOpen(mapInfo,current, x - 1, y - 1, OBLIQUE_VALUE);
            // 右上
            addNeighborNodeInOpen(mapInfo,current, x + 1, y - 1, OBLIQUE_VALUE);
            // 右下
            addNeighborNodeInOpen(mapInfo,current, x + 1, y + 1, OBLIQUE_VALUE);
            // 左下
            addNeighborNodeInOpen(mapInfo,current, x - 1, y + 1, OBLIQUE_VALUE);
        }
    
        /**
         * 添加一个邻结点到open表
         */
        private void addNeighborNodeInOpen(MapInfo mapInfo,Node current, int x, int y, int value)
        {
            if (canAddNodeToOpen(mapInfo,x, y))
            {
                Node end=mapInfo.end;
                Coord coord = new Coord(x, y);
                int G = current.G + value; // 计算邻结点的G值
                Node child = findNodeInOpen(coord);
                if (child == null)
                {
                    int H=calcH(end.coord,coord); // 计算H值
                    if(isEndNode(end.coord,coord))
                    {
                        child=end;
                        child.parent=current;
                        child.G=G;
                        child.H=H;
                    }
                    else
                    {
                        child = new Node(coord, current, G, H);
                    }
                    openList.add(child);
                }
                else if (child.G > G)
                {
                    child.G = G;
                    child.parent = current;
                    openList.add(child);
                }
            }
        }
    
        /**
         * 从Open列表中查找结点
         */
        private Node findNodeInOpen(Coord coord)
        {
            if (coord == null || openList.isEmpty()) return null;
            for (Node node : openList)
            {
                if (node.coord.equals(coord))
                {
                    return node;
                }
            }
            return null;
        }
    
    
        /**
         * 计算H的估值：“曼哈顿”法，坐标分别取差值相加
         */
        private int calcH(Coord end,Coord coord)
        {
            return Math.abs(end.x - coord.x)
                    + Math.abs(end.y - coord.y);
        }
    
        /**
         * 判断结点是否是最终结点
         */
        private boolean isEndNode(Coord end,Coord coord)
        {
            return coord != null && end.equals(coord);
        }
    
        /**
         * 判断结点能否放入Open列表
         */
        private boolean canAddNodeToOpen(MapInfo mapInfo,int x, int y)
        {
            // 是否在地图中
            if (x < 0 || x >= mapInfo.width || y < 0 || y >= mapInfo.hight) return false;
            // 判断是否是不可通过的结点
            if (mapInfo.maps[y][x] == BAR) return false;
            // 判断结点是否存在close表
            if (isCoordInClose(x, y)) return false;
    
            return true;
        }
    
        /**
         * 判断坐标是否在close表中
         */
        private boolean isCoordInClose(Coord coord)
        {
            return coord!=null&&isCoordInClose(coord.x, coord.y);
        }
    
        /**
         * 判断坐标是否在close表中
         */
        private boolean isCoordInClose(int x, int y)
        {
            if (closeList.isEmpty()) return false;
            for (Node node : closeList)
            {
                if (node.coord.x == x && node.coord.y == y)
                {
                    return true;
                }
            }
            return false;
        }
    }
    

• 36. Valid Sudoku

  Determine if a 9 x 9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:

  1. Each row must contain the digits 1-9 without repetition.
  2. Each column must contain the digits 1-9 without repetition.
  3. Each of the nine 3 x 3 sub-boxes of the grid must contain the digits 1-9 without repetition.

  Note:

  • A Sudoku board (partially filled) could be valid but is not necessarily solvable.
  • Only the filled cells need to be validated according to the mentioned rules.

  Input: board = 
  [["5","3",".",".","7",".",".",".","."]
  ,["6",".",".","1","9","5",".",".","."]
  ,[".","9","8",".",".",".",".","6","."]
  ,["8",".",".",".","6",".",".",".","3"]
  ,["4",".",".","8",".","3",".",".","1"]
  ,["7",".",".",".","2",".",".",".","6"]
  ,[".","6",".",".",".",".","2","8","."]
  ,[".",".",".","4","1","9",".",".","5"]
  ,[".",".",".",".","8",".",".","7","9"]]
  Output: true
  

  Example 2:

  Input: board = 
  [["8","3",".",".","7",".",".",".","."]
  ,["6",".",".","1","9","5",".",".","."]
  ,[".","9","8",".",".",".",".","6","."]
  ,["8",".",".",".","6",".",".",".","3"]
  ,["4",".",".","8",".","3",".",".","1"]
  ,["7",".",".",".","2",".",".",".","6"]
  ,[".","6",".",".",".",".","2","8","."]
  ,[".",".",".","4","1","9",".",".","5"]
  ,[".",".",".",".","8",".",".","7","9"]]
  Output: false
  Explanation: Same as Example 1, except with the 5 in the top left corner being modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.
  

  Constraints:

  • board.length == 9
  • board[i].length == 9
  • board[i][j] is a digit or '.'.

  class Solution {
      public boolean isValidSudoku(char[][] board) {
          boolean[][] rows = new boolean[9][9];
          boolean[][] cols = new boolean[9][9];
          boolean[][] blocks = new boolean[9][9];
          for (int i = 0; i < 9; i++) {
              for (int j = 0; j < 9; j++) {
                  if (board[i][j] == '.') continue;
                  if (rows[i][board[i][j] - '1']) return false;
                  if (cols[j][board[i][j] - '1']) return false;
                  int block = i/3 * 3 + j/3;
                  if (blocks[block][board[i][j] - '1']) return false;
                  rows[i][board[i][j] - '1'] = true;
                  cols[j][board[i][j] - '1'] = true;
                  blocks[block][board[i][j] - '1'] = true;
              }
          }
          return true;
      }
  }
  

• 37. Sudoku Solver

  Write a program to solve a Sudoku puzzle by filling the empty cells.

  A sudoku solution must satisfy all of the following rules:

  1. Each of the digits 1-9 must occur exactly once in each row.
  2. Each of the digits 1-9 must occur exactly once in each column.
  3. Each of the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.

  The '.' character indicates empty cells.

  Input: board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
  Output: [["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
  Explanation: The input board is shown above and the only valid solution is shown below:
  

  Constraints:

  • board.length == 9
  • board[i].length == 9
  • board[i][j] is a digit or '.'.
  • It is guaranteed that the input board has only one solution.

  class Solution {
      boolean[][] rows = new boolean[9][9];
      boolean[][] cols = new boolean[9][9];
      boolean[][] blocks = new boolean[9][9];
      char[] nums = {'1','2','3','4','5','6','7','8','9'};
      char[][] board;
      public void solveSudoku(char[][] board) {
          this.board = board;
          for (int i = 0; i < 9; i++) {
              for (int j = 0; j < 9; j++) {
                  if (board[i][j] == '.') continue;
                  rows[i][board[i][j] - '1'] = true;
                  cols[j][board[i][j] - '1'] = true;
                  blocks[i/3 * 3 + j/3][board[i][j] - '1'] = true;
              }
          }
          dfs(0, 0);
      }
  
      private boolean dfs(int i, int j) {
          if (j == 9){
              i++;
              j = 0;
              if (i == 9) return true;
          }
          if (board[i][j] != '.') {
              return dfs(i, j + 1);
          }
          for (char num : nums) {
              if (rows[i][num - '1'] || cols[j][num - '1'] || blocks[i/3 * 3 + j/3][num - '1']) {
                  continue;
              }
              board[i][j] = num;
              rows[i][num - '1'] = true;
              cols[j][num - '1'] = true;
              blocks[i/3 * 3 + j/3][num - '1'] = true;
              if (dfs(i, j + 1)) return true;
              rows[i][num - '1'] = false;
              cols[j][num - '1'] = false;
              blocks[i/3 * 3 + j/3][num - '1'] = false;
              board[i][j] = '.';
          }
          return false;
      }
  }
  

• 1091. Shortest Path in Binary Matrix

  Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

  A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

  • All the visited cells of the path are 0.
  • All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

  The length of a clear path is the number of visited cells of this path.

  Example 1:

  

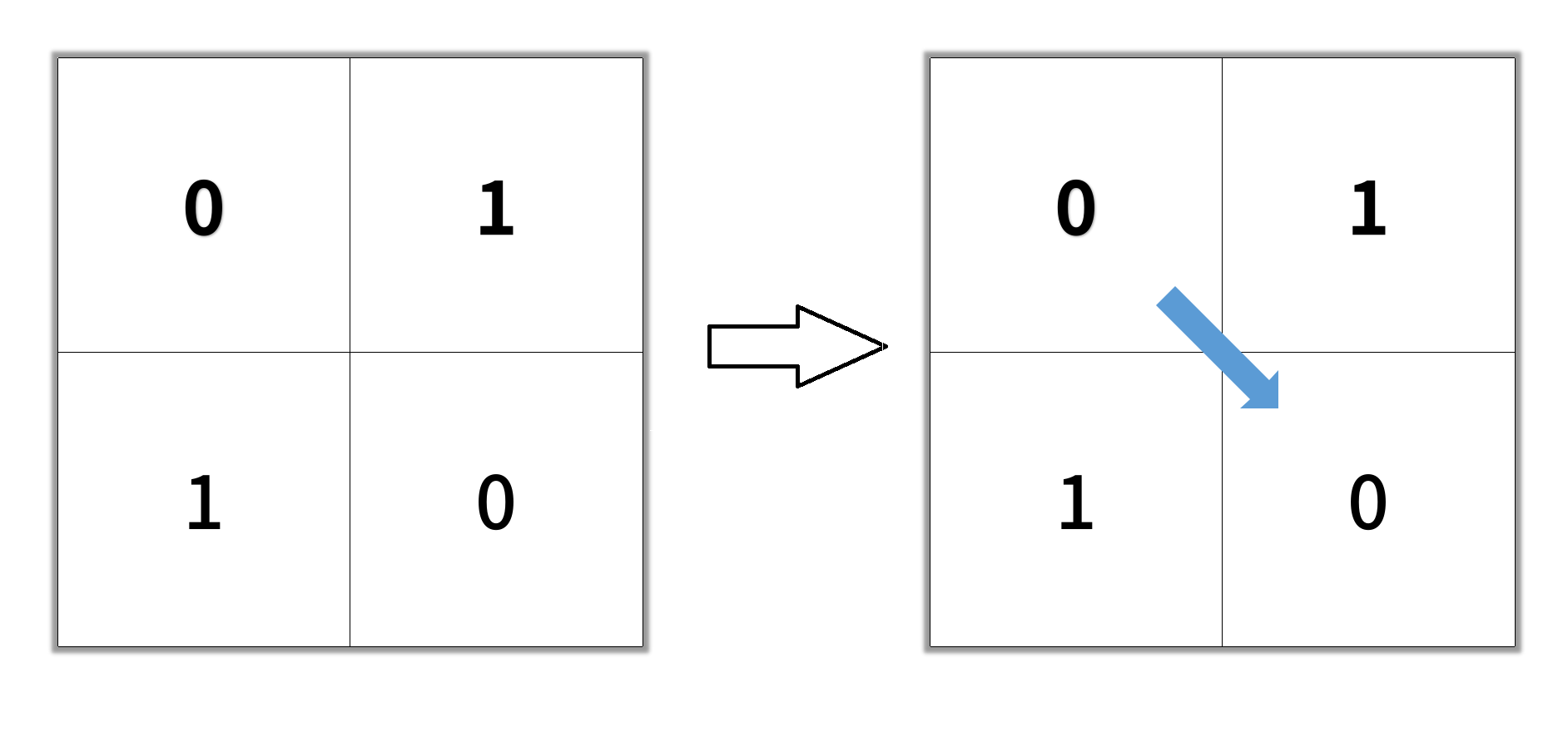
  Input: grid = [[0,1],[1,0]]
  Output: 2
  

  Example 2:

  

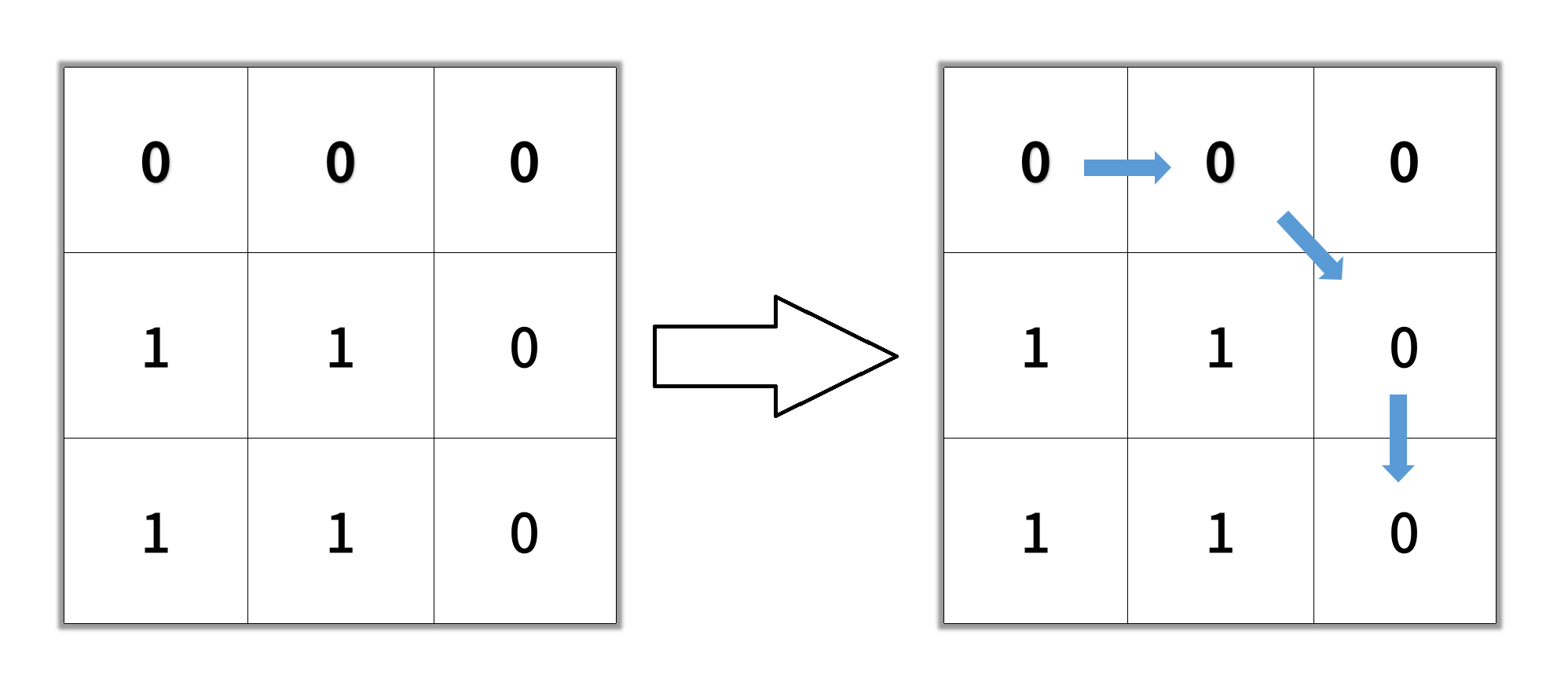
  Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
  Output: 4
  

  Example 3:

  Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
  Output: -1
  

  Constraints:

  • n == grid.length
  • n == grid[i].length
  • 1 <= n <= 100
  • grid[i][j] is 0 or 1

  class Solution {
      int[][] dirs = {{0,1},{0,-1},{1,0},{-1,0},{1,1},{1,-1},{-1,1},{-1,-1}};
      public int shortestPathBinaryMatrix(int[][] grid) {
          if (grid[0][0] == 1) return -1;
          Deque<int[]> deque = new LinkedList<>();
          int m = grid.length, n = grid[0].length;
          deque.addLast(new int[]{0,0});
          grid[0][0] = 1;
          int res = 0;
          while (!deque.isEmpty()) {
              int size = deque.size();
              res++;
              while (size-- > 0) {
                  int[] pos = deque.pollFirst();
                  int x = pos[0], y = pos[1];
                  if (x == m - 1 && y == n - 1) {
                      return res;
                  }
                  for (int[] dir : dirs) {
                      int i = x + dir[0], j = y + dir[1];
                      if (i >= 0 && i < grid.length && j >= 0 && j < grid[0].length && grid[i][j] == 0) {
                          deque.addLast(new int[]{i, j});
                          grid[i][j] = 1;
                      } 
                  }
              }
          }
          return -1;
      }
  }
  

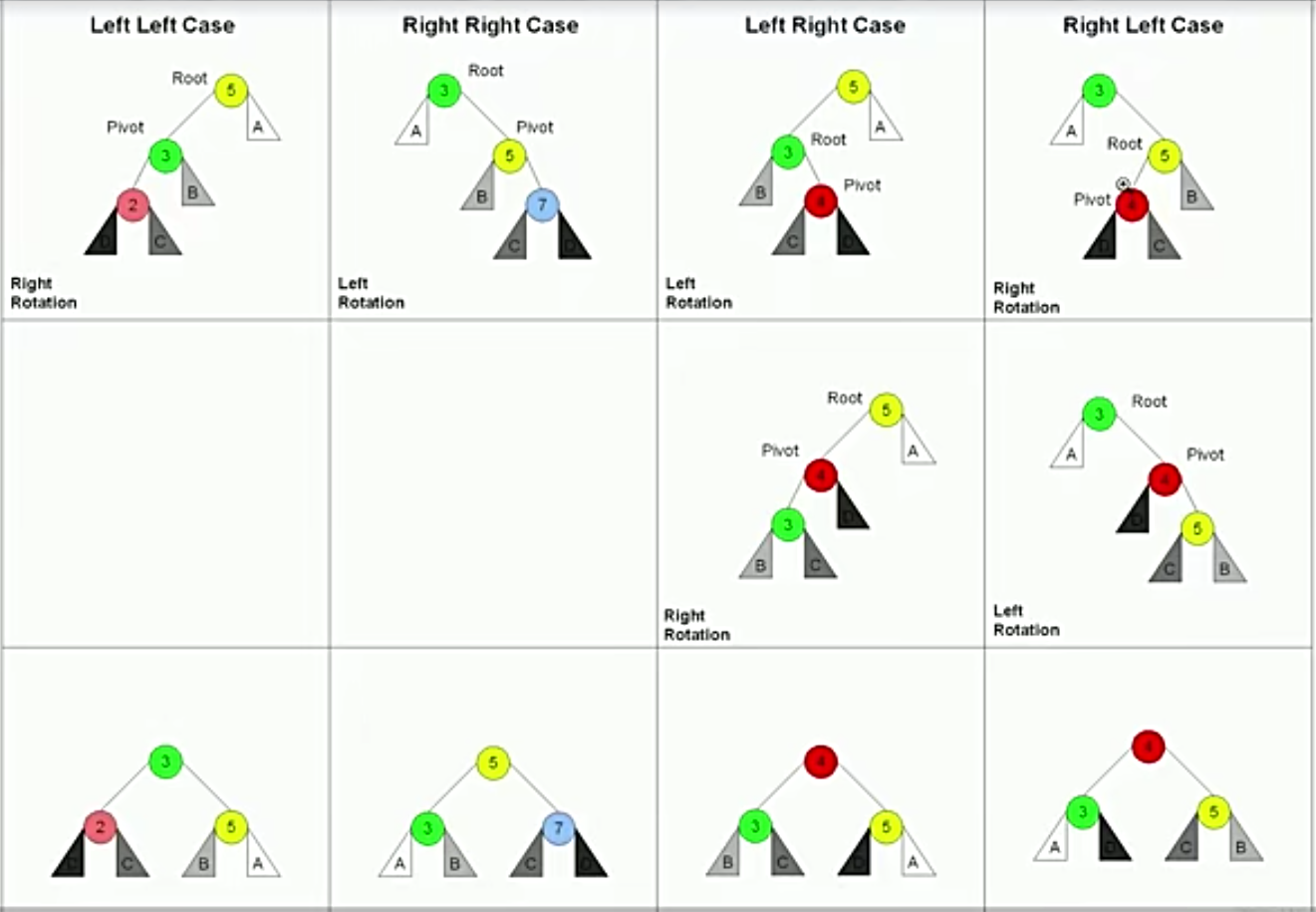
• AVL Tree

  

• Red Black Tree

  

  vs AVL Tree

  

• Bit Operation

  <<: 0011=>0110
  >>: 0110=>0011
  | : 0011|1011=>1011
  & : 0011&1011=>0011
  ~ : 0011=>1100
  ^ : 0011^1011=>1000
  
  x ^ 0 = x
  x ^ (~x) = (~0) = 1s(all one)
  x ^ 1s = ~x
  x ^ x = 0
  

  

  apply

  

• 191. Number of 1 Bits

  Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight).

  Note:

  • Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
  • In Java, the compiler represents the signed integers using 2's complement notation. Therefore, in Example 3, the input represents the signed integer. -3.

  Example 1:

  Input: n = 00000000000000000000000000001011
  Output: 3
  Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.
  

  Example 2:

  Input: n = 00000000000000000000000010000000
  Output: 1
  Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit.
  

  Example 3:

  Input: n = 11111111111111111111111111111101
  Output: 31
  Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits.
  

  Constraints:

  • The input must be a binary string of length 32.

  public class Solution {
      public int hammingWeight(int n) {
          int res = 0;
          while (n != 0) {
              res += (n&1) == 1 ? 1 : 0;
              n = n >>> 1;
          }
          return res;
      }
  }
  

• 231. Power of Two

  Given an integer n, return true if it is a power of two. Otherwise, return false.

  An integer n is a power of two, if there exists an integer x such that n == 2x.

  Example 1:

  Input: n = 1
  Output: true
  Explanation: 20 = 1
  

  Example 2:

  Input: n = 16
  Output: true
  Explanation: 24 = 16
  

  Example 3:

  Input: n = 3
  Output: false
  

  Example 4:

  Input: n = 4
  Output: true
  

  Example 5:

  Input: n = 5
  Output: false
  

  Constraints:

  • -231 <= n <= 231 - 1

  class Solution {
      public boolean isPowerOfTwo(int n) {
          return n > 0 && (n & (n - 1)) == 0;
      }
  }
  

• 190. Reverse Bits

  Reverse bits of a given 32 bits unsigned integer.

  Note:

  • Note that in some languages such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
  • In Java, the compiler represents the signed integers using 2's complement notation. Therefore, in Example 2 above, the input represents the signed integer -3 and the output represents the signed integer -1073741825.

  Follow up:

  If this function is called many times, how would you optimize it?

  Example 1:

  Input: n = 00000010100101000001111010011100
  Output:    964176192 (00111001011110000010100101000000)
  Explanation: The input binary string 00000010100101000001111010011100 represents the unsigned integer 43261596, so return 964176192 which its binary representation is 00111001011110000010100101000000.
  

  Example 2:

  Input: n = 11111111111111111111111111111101
  Output:   3221225471 (10111111111111111111111111111111)
  Explanation: The input binary string 11111111111111111111111111111101 represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is 10111111111111111111111111111111.
  

  Constraints:

  • The input must be a binary string of length 32

  public class Solution {
      // you need treat n as an unsigned value
      public int reverseBits(int n) {
          int res = 0;
          for (int i = 0; i < 32; i++) {
              res <<= 1;
              res += n & 1;
              n >>>= 1;
          }
          return res;
      }
  }
  

• 338. Counting Bits

  Given an integer num, return an array of the number of 1's in the binary representation of every number in the range [0, num].

  Example 1:

  Input: num = 2
  Output: [0,1,1]
  Explanation:
  0 --> 0
  1 --> 1
  2 --> 10
  

  Example 2:

  Input: num = 5
  Output: [0,1,1,2,1,2]
  Explanation:
  0 --> 0
  1 --> 1
  2 --> 10
  3 --> 11
  4 --> 100
  5 --> 101
  

  Constraints:

  • 0 <= num <= 105

  // stupid count
  class Solution {
      public int[] countBits(int num) {
          int[] res = new int[num + 1];
          for (int i = 1; i <= num; i++) {
              res[i] = countBit(i);
          }
          return res;
      }
  
      private int countBit(int num) {
          if (num == 0) return 0;
          return 1 + countBit(num & (num - 1));
      }
  }
  
  // DP
  class Solution {
      public int[] countBits(int num) {
          int[] bits = new int[num + 1];
          for (int i = 1; i <= num; i++) {
              bits[i] = bits[i >> 1] + (i & 1);
          }
          return bits;
      }
  }