Data Structure and Algorithm - Day 11
-
Trie
![]()
inner
![]()
-
208. Implement Trie (Prefix Tree)
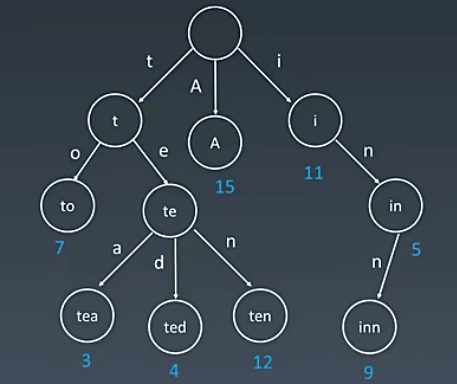
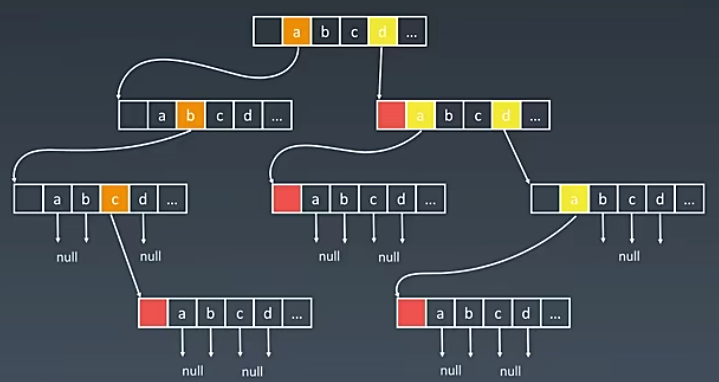
Trie (we pronounce "try") or prefix tree is a tree data structure used to retrieve a key in a strings dataset. There are various applications of this very efficient data structure, such as autocomplete and spellchecker.
Implement the Trie class:
Trie()initializes the trie object.void insert(String word)inserts the stringwordto the trie.boolean search(String word)returnstrueif the stringwordis in the trie (i.e., was inserted before), andfalseotherwise.boolean startsWith(String prefix)returnstrueif there is a previously inserted stringwordthat has the prefixprefix, andfalseotherwise.
Example 1:
Input ["Trie", "insert", "search", "search", "startsWith", "insert", "search"] [[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]] Output [null, null, true, false, true, null, true] Explanation Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // return True trie.search("app"); // return False trie.startsWith("app"); // return True trie.insert("app"); trie.search("app"); // return TrueConstraints:
1 <= word.length, prefix.length <= 2000wordandprefixconsist of lowercase English letters.- At most
3 * 104calls will be made toinsert,search, andstartsWith.
public class Trie { private boolean isString = false; private Trie[] next = new Trie[26]; public Trie() { } public void insert(String word) { Trie root = this; char[] w = word.toCharArray(); for (int i = 0; i < w.length; i++) { if (root.next[w[i] - 'a'] == null) root.next[w[i] - 'a'] = new Trie(); root = root.next[w[i] - 'a']; } root.isString = true; } public boolean search(String word) { Trie root = this; char[] w = word.toCharArray(); for (int i = 0; i < w.length; i++) { if (root.next[w[i] - 'a'] == null) return false; root = root.next[w[i] - 'a']; } return root.isString; } public boolean startsWith(String prefix) { Trie root = this; char[] p = prefix.toCharArray(); for (int i = 0; i < p.length; i++) { if (root.next[p[i] - 'a'] == null) return false; root = root.next[p[i] - 'a']; } return true; } } -
212. Word Search II
Given an
m x nboardof characters and a list of stringswords, return all words on the board.Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
Example 1:
![img]()
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"] Output: ["eat","oath"]Example 2:
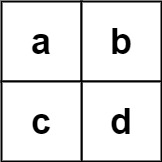
![img]()
Input: board = [["a","b"],["c","d"]], words = ["abcb"] Output: []Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 12board[i][j]is a lowercase English letter.1 <= words.length <= 3 * 1041 <= words[i].length <= 10words[i]consists of lowercase English letters.- All the strings of
wordsare unique.
class Solution { int[][] dirs = {{0,1},{0,-1},{1,0},{-1,0}}; Trie trie = new Trie(); public List<String> findWords(char[][] board, String[] words) { for (String word : words) { trie.insert(word); } Set<String> set = new HashSet<>(); StringBuilder sb = new StringBuilder(); for (int i = 0; i < board.length; i++) { for (int j = 0; j < board[0].length; j++) { dfs(set, sb, board, i, j); } } return new ArrayList<>(set); } private void dfs(Set<String> set, StringBuilder sb, char[][] board, int i, int j) { sb.append(board[i][j]); if (!trie.startsWith(sb.toString())) { sb.deleteCharAt(sb.length() - 1); return ; } if (trie.search(sb.toString())) { set.add(sb.toString()); } char t = board[i][j]; board[i][j] = '.'; for (int[] dir : dirs) { int x = i + dir[0], y = j + dir[1]; if (x >= 0 && x < board.length && y >= 0 && y < board[0].length && board[x][y] != '.') { dfs(set, sb, board, x, y); } } board[i][j] = t; sb.deleteCharAt(sb.length() - 1); } } class Trie {...} -
Disjoint Set
// Java Template class UnionFind { int count = 0; int[] parent; public UnionFind(int n) { count = n; parent = new int[n]; for (int i = 0; i < n; i++) { parent[i] = i; } } int find(int p) { while (p != parent[p]) { p = parent[parent[p]]; } return p; } void union(int p, int q) { int rootP = find(p); int rootQ = find(q); if (rootP != rootQ) { parent[rootP] = rootQ; count--; } } } -
547. Number of Provinces(Friend-Circles)
There are
ncities. Some of them are connected, while some are not. If cityais connected directly with cityb, and citybis connected directly with cityc, then cityais connected indirectly with cityc.A province is a group of directly or indirectly connected cities and no other cities outside of the group.
You are given an
n x nmatrixisConnectedwhereisConnected[i][j] = 1if theithcity and thejthcity are directly connected, andisConnected[i][j] = 0otherwise.Return the total number of provinces.
Example 1:
![img]()
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]] Output: 2Example 2:
![img]()
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]] Output: 3Constraints:
1 <= n <= 200n == isConnected.lengthn == isConnected[i].lengthisConnected[i][j]is1or0.isConnected[i][i] == 1isConnected[i][j] == isConnected[j][i]
class Solution { public int findCircleNum(int[][] isConnected) { int n = isConnected.length; UnionFind unionFind = new UnionFind(n); for (int i = 0; i < n; i++) { for (int j = i + 1; j < n; j++) { if (isConnected[i][j] == 1) { unionFind.union(i, j); } } } return unionFind.count; } } class UnionFind {...} -
200. Number of Islands
Given an
m x n2D binary gridgridwhich represents a map of'1's (land) and'0's (water), return the number of islands.An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] Output: 1Example 2:
Input: grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] Output: 3Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]is'0'or'1'.
class Solution { public int numIslands(char[][] grid) { int m = grid.length, n = grid[0].length; UnionFind unionFind = new UnionFind(m, n); int zero = 0; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (grid[i][j] == '0') { zero++; continue; } if (i-1 >= 0 && grid[i-1][j] == '1') { unionFind.union(i*n + j, (i-1)*n + j); } if (j-1 >= 0 && grid[i][j-1] == '1') { unionFind.union(i*n + j, i*n + j - 1); } if (j+1 < n && grid[i][j+1] == '1') { unionFind.union(i*n + j, i*n + j + 1); } if (i+1 < m && grid[i+1][j] == '1') { unionFind.union(i*n + j, (i+1)*n + j); } } } return unionFind.count - zero; } } class UnionFind { int count = 0; int[] parent; public UnionFind(int m, int n) { count = m * n; parent= new int[count]; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { parent[i*n + j] = i*n + j; } } } int find(int k) { while (parent[k] != k) { k = parent[parent[k]]; } return k; } void union(int p, int q) { int rootP = find(p); int rootQ = find(q); if (rootP != rootQ) { parent[rootP] = rootQ; count--; } } } -
130. Surrounded Regions
Given an
m x nmatrixboardcontaining'X'and'O', capture all regions surrounded by'X'.A region is captured by flipping all
'O's into'X's in that surrounded region.Example 1:
![img]()
Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]] Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]] Explanation: Surrounded regions should not be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.Example 2:
Input: board = [["X"]] Output: [["X"]]Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]is'X'or'O'.
class Solution { int[][] dirs = {{0,1},{0,-1},{1,0},{-1,0}}; public void solve(char[][] board) { int m = board.length, n = board[0].length; for (int i = 0; i < m; i++) { if (board[i][0] == 'O') { dfs(board, i, 0); } if (board[i][n-1] == 'O') { dfs(board, i, n-1); } } for (int j = 1; j < n-1; j++) { if (board[0][j] == 'O') { dfs(board, 0, j); } if (board[m-1][j] == 'O') { dfs(board, m-1, j); } } for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (board[i][j] == 'O') board[i][j] = 'X'; } } for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (board[i][j] == '.') board[i][j] = 'O'; } } } private void dfs(char[][] board, int i, int j) { board[i][j] = '.'; for (int[] dir : dirs) { int x = i + dir[0], y = j + dir[1]; if (x >= 0 && x < board.length && y >= 0 && y < board[0].length && board[x][y] == 'O') { dfs(board, x, y); } } } } -
213. House Robber II
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array
numsrepresenting the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.Example 1:
Input: nums = [2,3,2] Output: 3 Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.Example 2:
Input: nums = [1,2,3,1] Output: 4 Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3). Total amount you can rob = 1 + 3 = 4.Example 3:
Input: nums = [0] Output: 0Constraints:
1 <= nums.length <= 1000 <= nums[i] <= 1000
class Solution { public int rob(int[] nums) { if (nums.length == 1) return nums[0]; if (nums.length == 2) return Math.max(nums[0],nums[1]); int a = rob(nums, 0, nums.length - 2); int b = rob(nums, 1, nums.length - 1); return Math.max(a, b); } private int rob(int[] nums, int l, int r) { if (l == r) return nums[0]; if (l + 1 == r) return Math.max(nums[0],nums[1]); int[] dp = new int[r - l + 1]; dp[0] = nums[l]; dp[1] = Math.max(nums[l], nums[l+1]); for (int i = l+2; i <= r; i++) { dp[i-l] = Math.max(dp[i-l-1], dp[i-l-2]+nums[i]); } return dp[r-l]; } } -
121. Best Time to Buy and Sell Stock
You are given an array
priceswhereprices[i]is the price of a given stock on theithday.You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return
0.Example 1:
Input: prices = [7,1,5,3,6,4] Output: 5 Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5. Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.Example 2:
Input: prices = [7,6,4,3,1] Output: 0 Explanation: In this case, no transactions are done and the max profit = 0.Constraints:
1 <= prices.length <= 1050 <= prices[i] <= 104
class Solution { public int maxProfit(int[] prices) { int min = prices[0]; int res = 0; for (int i = 1; i < prices.length; i++) { res = Math.max(res, prices[i] - min); min = Math.min(min, prices[i]); } return res; } }







 浙公网安备 33010602011771号
浙公网安备 33010602011771号