10.21 双元数滤波器
下一个要研究的滤波器拓扑结构是双曲（或双曲）结构。双曲线由两个二阶组件组成：一个二阶前馈和一个二阶反馈滤波器组合在一起，如图10.44所示。由此产生的传递函数将有两个二次方程，因此得名。差分方程为：
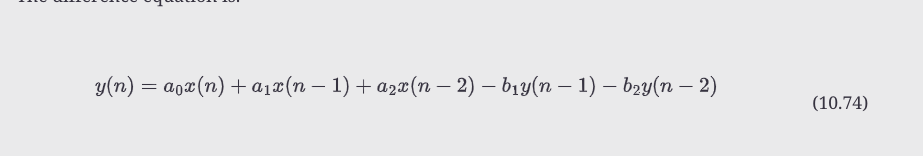
10.21.1 第1步、第2步和第3步：对差分方程进行z变换以获得传递函数，然后将a0作为标量增益系数进行分解。
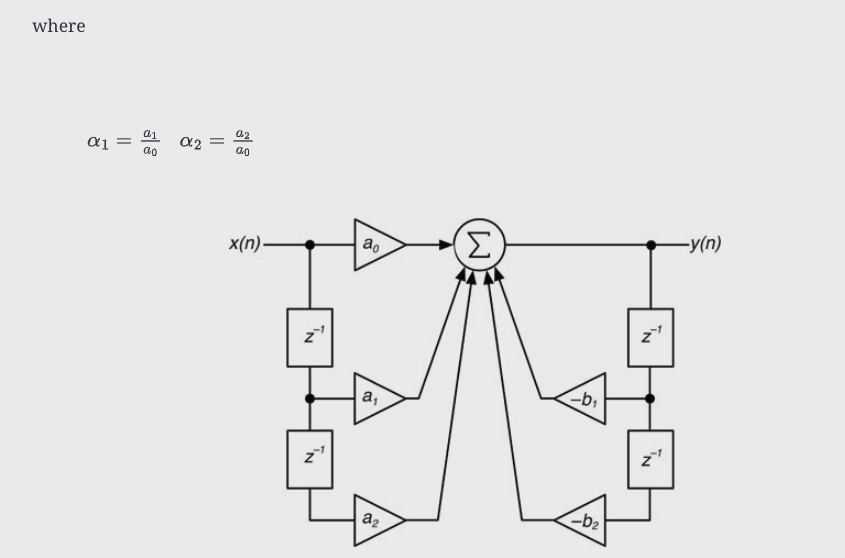
图10.44：二阶前馈和反馈部分相结合的双阙结构。
10.21.2 第四步：绘制传递函数的极点和零点图
biquad最多会从分子和分母中分别产生一对共轭的零点和一对共轭的极点。注意，你不需要使用完整的二阶部分；例如，你可能有一个算法，它有一个一阶前馈部分和一个二阶反馈部分。在这种情况下，你只需让a1项等于0.0，以有效地禁用其分支。计算这些极点和零点的位置与纯二阶前馈和反馈拓扑结构是一样的。你所需要做的就是将它们绘制在同一个单位圆内。传递函数成为（通过前几节的简单替换）方程10.76的函数。
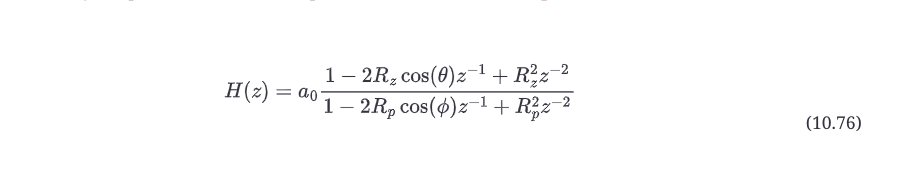
我们可以绘制一对任意的极点和零点，如图10.45a所示；每个极点都有自己的半径Rz和Rp，以及角度θ和φ。
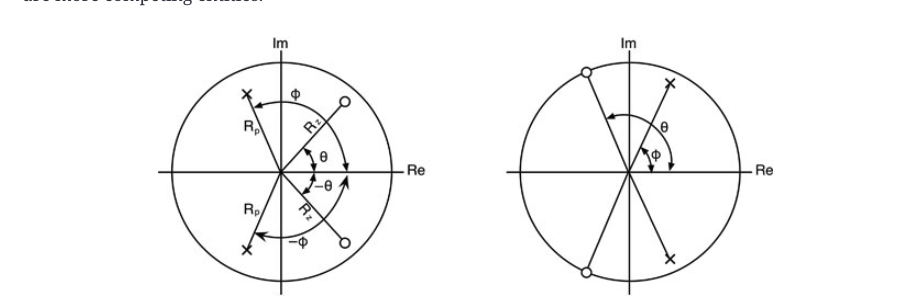
图10.45：(a)在Z平面上绘制的一对任意共轭的极点和零点。(b)我们的双叉体例子的极点/零点图。
由于有额外的极点和零点，估计频率响应是复杂的，但过程是相同的。
在单位圆的外缘找到每个评估频率。
从圆上的点到每个零点画一条线，测量这些向量的长度。对每个评价频率都这样做。
从圆上的点到每个极点画一条线，测量这些向量的长度。对每个评估频率都要这样做。
将所有的零点幅度相乘。
将所有的反极点幅度相乘。
用零点幅度除以极点幅度，得出该频率下的最终结果。
为了演示，使用以下系数。
a0 = 1.0
a1 = 0.73
a2 = 1.00
b1 = -0.78
b2 = 0.88
我们可以直接从公式10.76中找到极点和零点的位置（注意，因为a0是1.0，你不必计算α项）。图10.45b中画出了这对极点和零点。
图10.44：二阶前馈和反馈部分相结合的双阙结构。
10.21.2 第四步：绘制传递函数的极点和零点图
biquad最多会从分子和分母中分别产生一对共轭的零点和一对共轭的极点。请注意，你不需要使用完整的二阶部分；例如，你可能有一个算法，它有一个一阶前馈部分和一个二阶反馈部分相结合。在这种情况下，你只需让a1项等于0.0，以有效地禁用其分支。计算这些极点和零点的位置与纯二阶前馈和反馈拓扑结构是一样的。你所需要做的就是将它们绘制在同一个单位圆内。传递函数成为（通过前几节的简单替换）方程10.76的函数。
我们可以绘制一对任意的极点和零点，如图10.45a所示；每个极点都有自己的半径Rz和Rp，以及角度θ和φ。
图10.45：(a)在Z平面上绘制的一对任意共轭的极点和零点。(b)我们的双叉体例子的极点/零点图。
由于额外的极点和零点，估计频率响应是复杂的，但过程是一样的。
在单位圆的外缘找到每个评估频率。
从圆上的点到每个零点画一条线，测量这些向量的长度。对每个评价频率都这样做。
从圆上的点到每个极点画一条线，测量这些向量的长度。对每个评估频率都要这样做。
将所有的零点幅度相乘。
将所有的反极点幅度相乘。
用零点幅度除以极点幅度，得出该频率下的最终结果。
为了演示，使用以下系数。
a0 = 1.0
a1 = 0.73
a2 = 1.00
b1 = -0.78
b2 = 0.88
我们可以直接从公式10.76中找到极点和零点的位置（注意，因为a0是1.0，你不必计算α项）。图10.45b中画出了这对极点和零点。
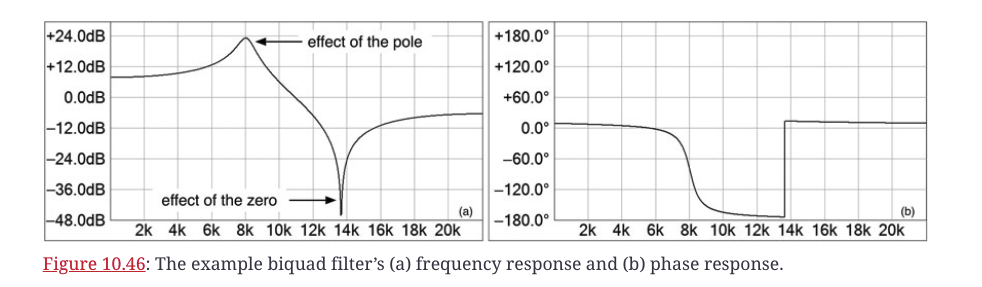
图10.46：例子中的biquad滤波器的（a）频率响应和（b）相位响应。
零点的计算方法如下。
极点和零点相对地接近对方。零点直接在单位圆上（Rz=1.0），所以我们预计在零点频率上会出现一个缺口。极点靠近单位圆，但没有接触到它，所以我们预计在极点频率上会出现共振。在图10.46a中，我们很容易找到极点或零点非常占优势的地方。在低频时，极点占优势，在高频时，零点占优势。请注意，图10.46b中突然出现的相位响应变化与峰值和凹槽位置相对应。这是一个直接Z面设计的例子，我们直接在Z面放置一个极点和零点对，然后计算系数。
10.21.3 aN和bM系数的命名规则
在继续之前，有一个简单的项目要介绍：aN和bM系数在各种DSP书籍中是如何命名的。你可以看到，在这本书中，分子系数用字母a命名，分母系数用字母b命名。a0系数是滤波器增益标量，从来没有b0系数。对于一些DSP工程师来说，这是一个令人痛心的话题：原因是如果你买了10本不同的DSP书籍，其中一半会使用我们这里的惯例，而另一半则会把as和b换掉，似乎把传递函数颠倒了，使差分方程显得不正确。我在这里使用命名规则的原因很简单：在我上大学时，我的模拟和数字滤波教科书都是这样命名的，而且我也一直是这样命名的。如果所有的DSP教科书作者都同意这样做就好了，但在此之前，当你看其他书籍和论文时，要确保你了解所使用的命名规则。这实际上相当简单：如果你看到一个b0系数，那么他们使用的是 "分子中的bs "惯例。
10.22 其他双曲线结构
图 10.44 中的结构被称为直接形式（DF）结构。它直接实现了差分方程，你可以在一个方程中一次性形成输出y(n)。你可能写的实现这个结构的伪代码可能是这样的。
// -- 直接形成输出
yn = a0*xn + a1*x(n-1) + a2*x(n-2)-b1*y(n-1)-b2*y(n-2)
// -- 更新状态寄存器
x(n-2) = x(n-1)
x(n-1) = xn
y(n-2) = y(n-1)
y(n-1) = yn
事实证明，直接形式结构只是几种结构中的一种，它们也会产生正确的差分方程。还有三种常用的结构，如图10.47所示。这些结构包括典范形式和转置形式。双二次传递函数有一个分子多项式，最大多项式指数为2，分母也是如此。传递函数的阶数是分子或分母的最大阶数--以最大者为准。对于biquad来说，其阶数是2。一个典型的结构包含的Z-1状态寄存器的数量与传递函数的阶数完全相同；这意味着分子和分母最终共享两个状态寄存器。你可以在图10.47所示的典型形式（CF）中看到这一点，它只使用了两个状态寄存器。为了创建结构的转换版本，我们将结构的节点转换为和值，将和值转换为节点，并将箭头的方向相反。你可以在图10.47中的转置的直接形式和转置的典型形式中看到这一点。所有四种双元组框图在输出端产生相同的差分方程。许多DSP工程师根据其计算效率、内存存储要求和对系数中舍入误差的敏感性对结构进行分类。结构本身--求和与乘法节点的排序--也会对y(n)的最终计算的准确性产生影响。高阶多项式对系数误差更敏感--因此当面对一个高于二阶的传递函数时，我们在数学上将传递函数拆分为一阶和二阶结构的一系列连接。一个三阶的滤波器是由一阶和二阶的结构串联实现的，而一个十阶的传递函数则是由五个二阶段串联实现的。我们应该注意到，我们所有的C++ FX对象都将使用双精度系数、双精度状态寄存器和双精度数学处理，所以我们不像定点DSP系统那样容易受到这些问题的影响，现在很多音频应用中仍然存在这些问题。
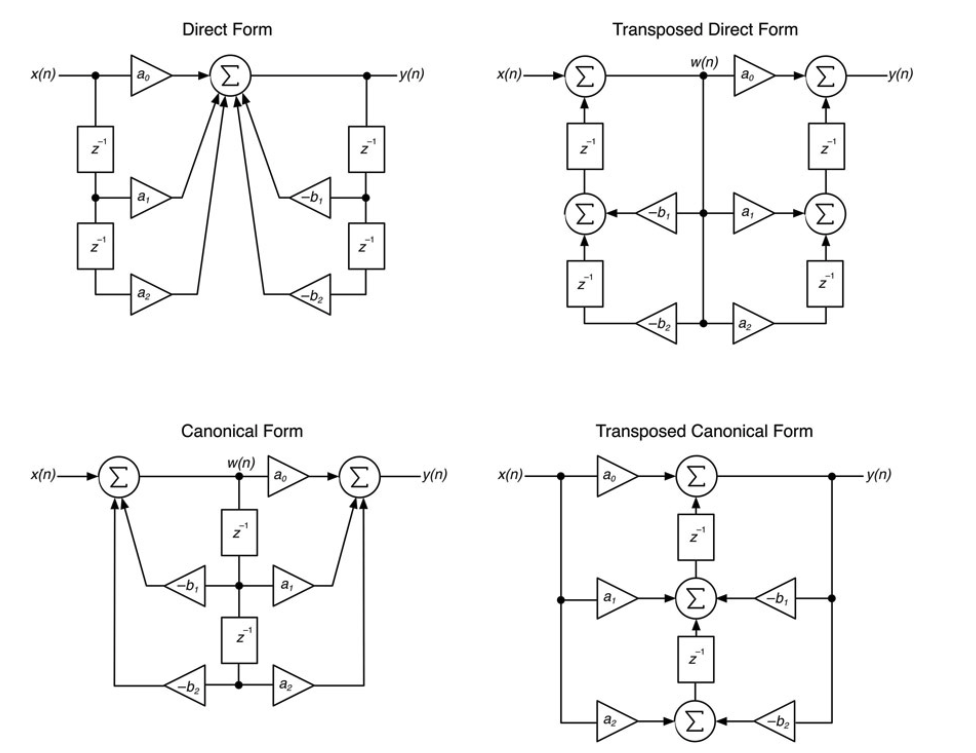
图10.47：实现双曲线传递函数的四种最常用的结构。
直接形式（直接形式和转置的直接形式）是最简单的实现方式，但也是最容易出错的。转置的典型形式一般被认为是浮点实现的最佳结构，这是因为多个和值的分工方式，增加了类似大小的数值。使用各种结构的滤波器频率的调制也有利弊，特别是当调制值快速变化时。
10.23 C++ DSP对象。Biquad
现在是时候看看我们的第一个C++的DSP对象，名为Biquad。这个对象实现了所有四个标准形式，并默认为直接形式。每个项目附带的fxobjects.h和fxobjects.cpp文件都充满了C++对象，用于处理本书中所有项目的信号处理工作。这些C++对象都符合第8章讨论的IAudioSignalProcessor的要求。
10.23.1 Biquad: 枚举和数据结构
Biquad对象有两个成员变量，是double 类型的数组。一个数组用于存储滤波器系数a0、a1、a2、b1和b2，此外还有两个我们将在更复杂的滤波器算法中使用的系数c0和d0。另一个数组存储滤波器的状态变量值，或者说Z-1寄存器信息。我们使用两个标准的枚举来访问每个数组中的槽。
// -- 系数的索引值
// a0 = 0, a1 = 1, a2 = 2, b1 = 3, b2 = 4, numCoeffs = 5
enum filterCoeff {a0, a1, a2, b1, b2, c0, d0, numCoeffs};
// ---状态数组索引值
enum {x_z1, x_z2, y_z1, y_z2, numStates}
我们使用一个强类型的枚举来描述我们正在实现的特定的biquad形式。枚举值的命名与它们所代表的形式完全一致，前面的 "k "代表 "常量"。
// -- 计算类型（算法）
enum class biquadAlgorithm {kDirect, kCanonical, kTransposeDirect,
kTransposeCanonical}。
自定义数据结构很简单--它只保存biquad算法的计算类型变量，使用强类型的枚举。
struct BiquadParameters
{
BiquadParameters () {}
BiquadParameters& operator=(const BiquadParameters& params) {...}。
// --- 一个也是唯一的变量是重新计算的标志
biquadAlgorithm biquadCalcType = biquadAlgorithm::kDirect;
};
10.23.2 Biquad: 成员
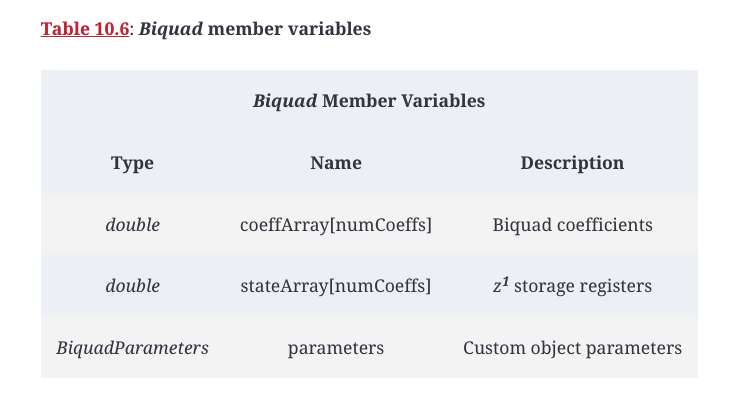
表10.6和10.7列出了Biquad的成员变量和成员函数。
10.23.3 Biquad: 编程注意事项
注意我们在setCoefficients函数中传递了一个指向biquad系数数组的指针，该函数使用批量内存拷贝来设置数组--这意味着必须注意总是使用一个大小与状态数组大小一致的数组，也就是numCoeffs。还要注意setParameter参数是如何与成员变量的名称相同的，但前面有一个下划线"_"；这种命名模式将被经常使用。
IAudioSignalProcessor
reset: 冲洗状态数组，将零载入状态寄存器中。
canProcessAudioFrame：返回false，因为我们只处理样本。
表10.6：Biquad成员变量
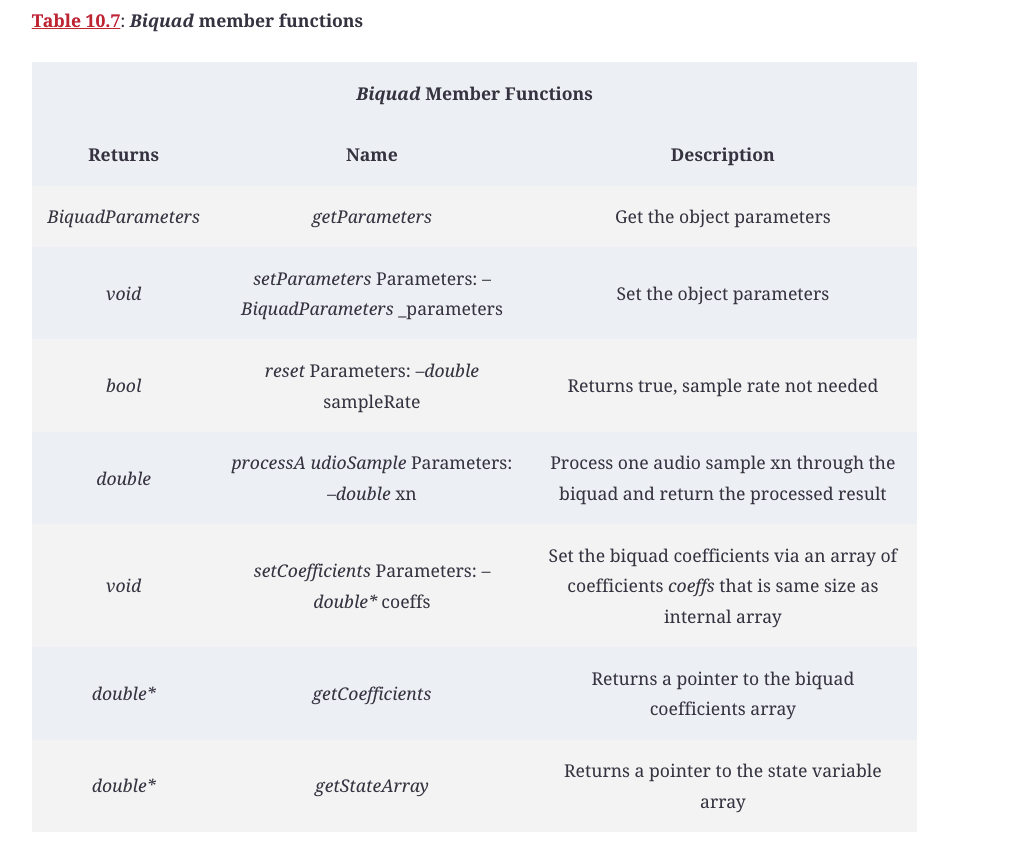
所有的工作都在processAudioSample函数中，它接受输入参数x(n)并计算一个返回变量y(n)。让我们看一下实现直接形式算法的第一部分。对于每个算法，我们将遵循一个固定的模式。
从状态寄存器中读取变量，并做任何需要制定输出y(n)的事情；这可能只是一行代码，也可能是很多行。
使用fxobjects.h中声明的一个辅助函数，检查y(n)的值是否有浮点下溢。
只有在y(n)的最终值准备好之后，我们才会更新状态寄存器，以正确的顺序推入数据以保持状态寄存器的关系。
我们首先将参数.biquadCalcType变量与强类型的枚举常量进行比较，并相应地进行分支。对于直接形式，顺序很简单。
使用当前输入x(n)、位于状态数组中的先前输入和输出以及位于系数数组中的系数，一次性创建y(n)。
检查是否有下溢。
依次更新状态寄存器，从最古老的到最年轻的样本值。
注意使用枚举（a0，a1等）使访问系数变得容易，使用状态数组的枚举（x_z1，x_z2等）来访问这些数据。
将yn的计算与图10.47中的算法进行比较，确保你能看到这行代码是如何正确计算y(n)的。
注意数据是如何通过状态数组进行洗牌的。
double Biquad::processAudioSample(double xn)
{
if(parameters.biquadCalcType == biquadAlgorithm::kDirect)
{
// y(n) = a0*x(n) + a1*x(n-1) + a2*x(n-2) -b1*y(n-1)
// -b2*y(n-2)
double yn = coeffArray[a0] * xn +
coeffArray[a1] * stateArray[x_z1] +
coeffArray[a2] * stateArray[x_z2] -
coeffArray[b1] * stateArray[y_z1]-
coeffArray[b2] * stateArray[y_z2]。
// -- 2) 下溢检查
checkFloatUnderflow(yn);
// -- 3) 更新状态
stateArray[x_z2] = stateArray[x_z1];
stateArray[x_z1] = xn;
stateArray[y_z2] = stateArray[y_z1];
stateArray[y_z1] = yn。
// -- 返回值
return yn。
}
现在让我们来看看图10.48a所示的典型形式，它有点棘手。注意图10.48b中的状态寄存器是如何标记的：上面的z-1寄存器是x_z1，下面的是x_z2。这就是状态数组中使用的两个索引位置。
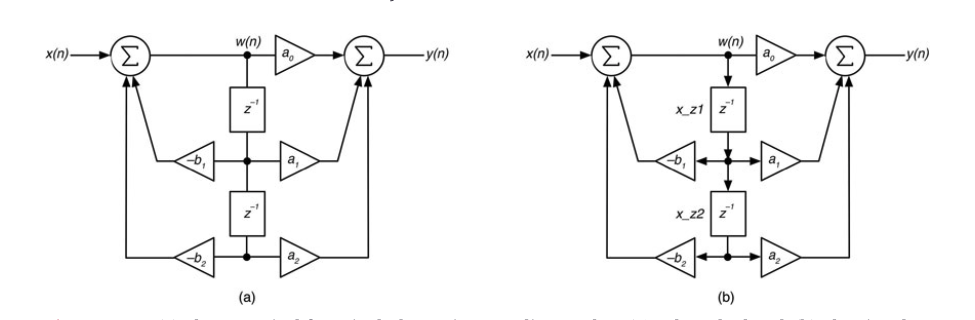
图10.48：（a）典型形式包括要计算的中间节点w（n）。(b) 通过该结构的信号流。
当遇到这些算法时，只需记住遵循前面列出的步骤。第一次尝试实现这些算法时，很容易让你的头脑陷入无限循环。在计算完y(n)之前，不要轻易将任何数据推入任何状态寄存器--这通常会解决你的无限循环问题。在图10.48b中，我们添加了箭头来显示数据和分支值的流动，以演示如何计算它们，但这导致了一个过度装饰的图。一般来说，我们只在箭头是输入和的时候才会显示。对于典型的形式，问自己中间节点w(n)需要什么信息。答案是，w(n)是一个夏天的输出，这个夏天有三个输入，都在图10.48b中标明。确保你能调和图10.48b如何转化为w(n)节点的这行代码；减号是因为b系数在算法中被否定了。
else if (parameters.biquadCalcType == biquadAlgorithm::kCanonical)
{
double wn = xn-(coeffArray[b1]*stateArray[x_z1])
-（coeffArray[b2]*stateArray[x_z2]);
现在把你的注意力转向y(n)。我们需要什么来计算它？确保你能找出这行代码来计算y(n)。
double yn = coeffArray[a0]*wn
+ coeffArray[a1]*stateArray[x_z1]
+ coeffArray[a2]*stateArray[x_z2]
计算出y(n)后，我们就可以更新状态。看一下图10.48b。上层z-1寄存器的输入值是什么？答案是w(n)。下层z-1寄存器的输入值是什么？它是上层寄存器的输出。这意味着，在我们将w(n)的数据移入下层寄存器之前，我们不能将其写入上层寄存器。这段代码就在这里。
// -- 3) 更新状态
stateArray[x_z2] = stateArray[x_z1];
stateArray[x_z1] = wn;
// --- 返回值
return yn。
}
其余两个算法的代码如下。请确保你能将代码与图10.47中的框图联系起来。
else if (parameters.biquadCalcType ==
biquadAlgorithm::kTransposeDirect)
{
// -- w(n) = x(n) + stateArray[y_z1]。
double wn = xn + stateArray[y_z1];
// --- y(n) = a0*w(n) + stateArray[x_z1].
double yn = coeffArray[a0] * wn + stateArray[x_z1];
// -- 2) 下溢检查
checkFloatUnderflow(yn);
// -- 3) 更新状态
stateArray[y_z1] = stateArray[y_z2]-coeffArray[b1] * wn;
stateArray[y_z2] = coeffArray[b2] * wn;
stateArray[x_z1] = stateArray[x_z2] + coeffArray[a1] * wn;
stateArray[x_z2] = coeffArray[a2] * wn;
// -- 返回值
return yn。
}
else if （parameters.biquadCalcType ==
biquadAlgorithm::kTransposeCanonical)
{
// -- 1) 形式输出 y(n) = a0*x(n) + stateArray[x_z1] 。
double yn = coeffArray[a0]*xn + stateArray[x_z1]。
// -- 2)下溢检查
checkFloatUnderflow(yn);
// -- 洗牌/更新
stateArray[x_z1] = coeffArray[a1]*xn
- coeffArray[b1]*yn + stateArray[x_z2]。
stateArray[x_z2] = coeffArray[a2]*xn-coeffArray[b2]*yn;
// -- 返回值
return yn
}
使用Biquad对象是很简单的。
重置该对象，为流媒体做准备。
在BiquadParameters自定义数据结构中设置计算类型。
调用setParameters来更新计算类型。
调用processAudioFrame，将输入值传入并接收输出值作为返回变量。
10.24 家庭作业
反馈拓扑结构
对于一个给定的双向传递函数H(z)，可以证明在一个给定的归一化频率ω处的幅度平方响应|H(z)|2，这样（0.0 ≤ ω ≤ π）可以计算为。
(10.79)
编写一个C++函数，在给定的评估频率ω和一组双曲系数a0、a1、a2、b1和b2的情况下，计算出幅度H(z)（dB）。你需要取方程10.79结果的平方根，然后转换为dB。如果你擅长制图，可以写一个程序，在给定的滤波器系数范围内，在ω=0.0到ω=π的范围内，绘制出任何biquad的幅度（dB）。你可以尝试在这个范围内均匀地分布各种评估频率，例如，以π/10的增量从0到π的11个评估频率。
还有其他几种算法可以实现双二次传递函数。有一种非常有趣的算法是从第12章的波浪数字滤波器中得到的。其框图如图10.49所示。
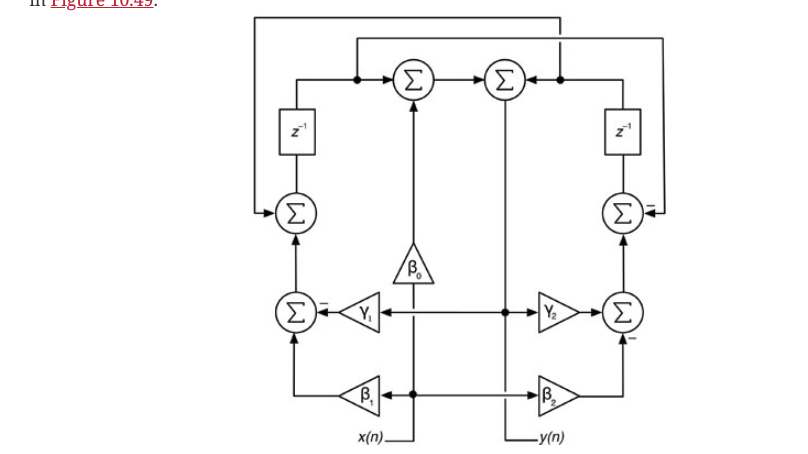
图10.49：由二阶波数字滤波器衍生出的双阙结构。
图10.49中的系数方程与biquad系数aN和bM的关系如下。
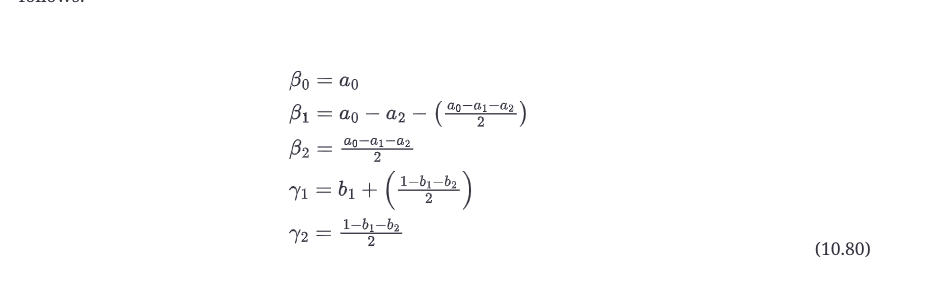
修改Biquad对象来实现这个额外的算法。你可以在我们实现第11章的音频滤波器时测试它。确保你遵循关于算法中操作顺序的规则。
10.25 Bibliography
Ifeachor, E. C. and Jervis, B. W. 1993. Digital Signal Processing: A Practical Approach, Chap. 3. Menlo Park: Addison Wesley.
Kwakernaak, H. and Sivan, R. 1991. Modern Signals and Systems, Chap. 3. Eaglewood Cliffs: Prentice-Hall.
Moore, R. 1990. Elements of Computer Music, Chap. 2. Eaglewood Cliffs: Prentice-Hall.
Oppenheim, A. V. and Schafer, R. W. 1999. Discrete-Time Signal Processing, 2nd Ed., Chap. 3. Eaglewood Cliffs: Prentice-Hall.
Orfanidis, S. 1996. Introduction to Signal Processing, Chap. 10–11. Eaglewood Cliffs: Prentice-Hall.
Schlichthärle, D. 2011. Digital Filters Basics and Design, 2nd Ed., Chap. 5. Heidelberg: Springer.
Steiglitz, K. 1996. A DSP Primer with Applications to Digital Audio and Computer Music, Chap. 4–5. Menlo Park: Addison Wesley.
