你想掌握滤波器的DSP基础理论有几个原因:了解滤波器的解剖结构有帮助,因为你想在新的滤波器设计出现时就能实现它,而不是等别人来编码;对理论的深入理解只能帮助你的编码策略;同样的DSP分析和数学模型可以应用于各种非EQ效果,如延迟、合唱、混响和压缩。为了直观地理解DSP理论的基础,你需要回顾一些数学和工程概念。
10.1 复数正弦波
数字滤波器的分析和设计使用正弦波作为其基本刺激函数。由于傅里叶表明信号可以被分解成正弦波,如果你知道系统对一堆不同频率的正弦波刺激的反应,你可以像上一章中手工绘制频率和相位响应。这类似于使用脉冲响应:因为输入信号是一列振幅不同的脉冲,如果你知道滤波器对单个脉冲的反应,你就可以算出它对多个脉冲的反应。在上一章取低通滤波器的脉冲响应时,你也用手做了这个。
每个人都熟悉正弦和余弦函数--正弦和余弦的关系是偏移90度,正弦函数的起点是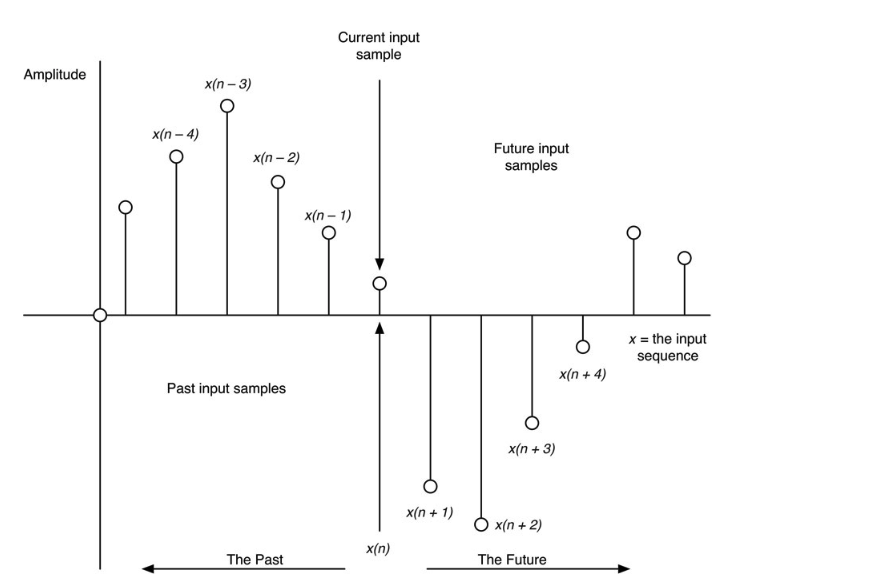
0.0,而余弦的起点是1.0。在图10.1a中,你可以通过正弦和余弦的起始位置来识别它们的波形。
但在图10.1b中,你如何称呼一个在任意时间开始的正弦波?它是一个向后移位的正弦,还是一个向前移位的余弦?你必须小心回答,因为正弦和余弦有不同的数学特性:它们的导数是不一样的,当你试图将它们相乘或以复杂的方式组合时,通常会变得困难。在sin()或cos()函数的参数上加上一个相位偏移,然后当你用它们做代数和微积分时,就真的变成了一团糟。你需要的是一个以正弦方式表现的函数,它封装了正弦和余弦函数,并且在数学上容易处理。这样的函数是存在的,它被称为复数正弦体。
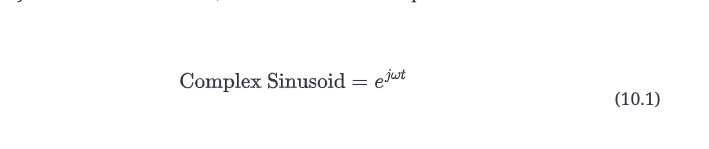
你可能会认识到这涉及到欧拉方程
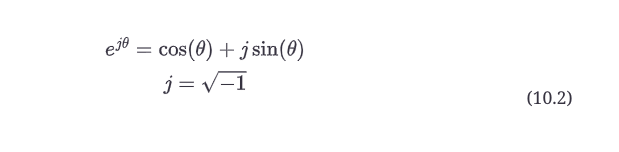
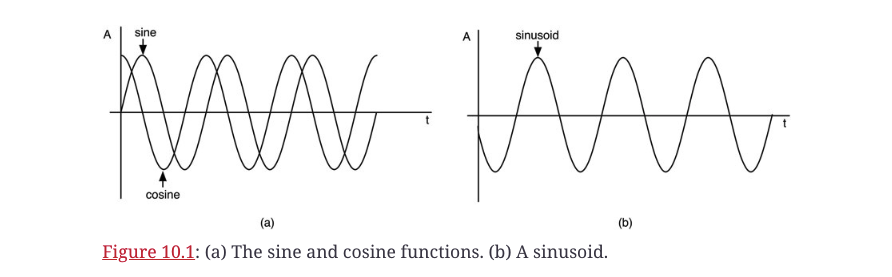
你可以看到,它包括正弦和余弦函数。j项是虚数,是-1的平方根(数学家称之为i,但由于我们在工程中已经用它作为电流的符号,所以我们改称j)。j被称为相位旋转算子;将一个函数乘以j,相位旋转90度。
假设你想将一个波形的相位移动180度,从而将其倒置。在数学上,你可以通过将波形乘以-1来做到这一点,将其所有点的值倒置。假设你想再次反转波形(这将使它恢复到原来的形状):你可以通过再次乘以-1来实现。但是,假设你只想把相位移动90度?是否有一个数字η可以作为乘数来移位90度?换句话说。
90度移位后的波形=(原波形)(η)
你还不知道η是什么,但你可以算出来。假设你想把波形再移90度,这就相当于把原波形移180度。你会再次将其乘以η。然后你就会得到以下结果。

这导致了公式10.3。

因此,你可以通过将一个波形乘以j来完成一个概念上的90度相移,而90度相移是通过乘以-j来完成的。其他一些与j有关的有用的关系是。
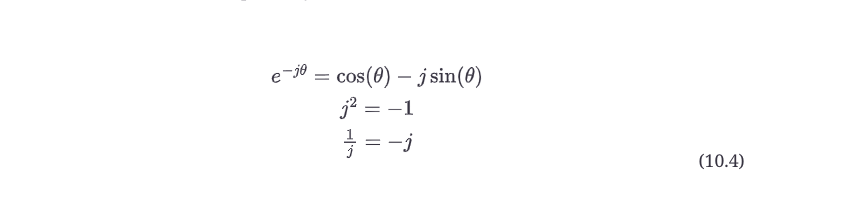
欧拉方程是复数,包含实数部分(cos)和虚数部分(sin)--方程中的加号(+)不是字面上的加法(你不能把实数和虚数加在一起)。在格式为a+jb的复数中,这两部分作为一个复数的一部分而共存。
因此,欧拉方程真正描述的是一对正弦和余弦函数,共存于相距90度的两个平面。正交这个词一般涉及相距90度或成直角的事物。在数学上,如果两个函数的内积为零,它们就是正交的。当这种情况发生时,这两个函数是最大的不相似。这意味着从数学上讲,sin和cos就像黑夜和白天、热和冷等一样不相似。
为了我们的目的,我们用ωt代替欧拉方程中的Θ,其中ω是弧度/秒的频率,t是时间变量。插入不同的t值,当你在同一平面上绘制正弦和余弦时,你会得到图10.1中的图形。因此,我们将拒绝独立使用sin()和cos()函数,而采用复数正弦作为这两者的预包装混合物。我们在这里的动机有一部分是数学上的,因为事实证明,e在数学上很容易处理,而sin和cos一旦开始在更高的数学层次上操作它们就会变得很困难。除了欧拉方程(也叫欧拉定理)之外,你只需要学习方程10.5中的四条规则。

方程10.5中的前两个方程表明,即使参数是时间的函数t,e的行为也像一个多项式(x2*x5=x^7),下一对方程表明它在微积分中的行为是多么简单。在我们离开这个话题之前,确保你记得如何处理复数--你将需要它来理解频率和相位响应的来源。
10.2 复数数学复习
因为复数有实部和虚部,所以不能在单轴上作图。为了绘制复数,你需要两条轴--实轴和虚轴。这两条轴呈直角排列,就像二维几何中的X轴和Y轴。它们是正交的。X维是实轴(Re),Y维是虚轴(Im)。因此,一个复数被绘制成这个X-Y平面上的一个点,也被称为复平面。复数通常被写成a+jb的形式,其中a是实部,b是虚部。请注意,即使常识可能与之相悖,符号也总是保持在a+jb的形式中。对于第二象限的点,你仍然写-2+j2,尽管j2-2可能看起来更漂亮。另外注意,我将写2-j1,而不是2-j,以确定虚数部分b=1。如图10.2a所示,这些点是按照你在平面上绘制(x,y)对的方式绘制的。图10.2a将点绘制成(x+jy)对--这被称为笛卡尔坐标系。你也可以使用极坐标符号来识别相同的复数。在极坐标符号中,你要指定从轴的原点向外画线到有关点的矢量的半径(R)和角度(Θ)。例如,考虑图10.2a中的点2+j3。你可以用极坐标形式绘制这个点,如图10.2b。我们留下笛卡尔形式(2 + j3)作为参考。通常情况下,你看到的只是R和Θ。大多数工程师在处理复数时喜欢用极坐标符号。极数通常被写成R < Θ 幸运的是,对我们来说,从笛卡尔符号到极数符号的转换很简单。从形式为a+jb的复数开始,你可以用公式10.6求出结果的半径和角度。你可以用公式10.6的后半部分将极坐标转换为直角坐标。我们将在第20章的相位转换器(pitch shifter)对象中进行这种类型的转换。
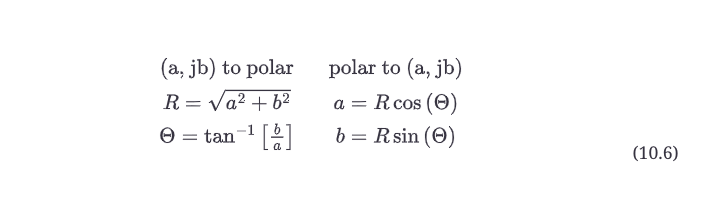
半径(R)被称为幅度,角度(Θ)被称为参数、相位、相位角,或者更简单的角度。有时你只关心幅值的平方(称为幅值平方或|R|2),如公式10.7所示。
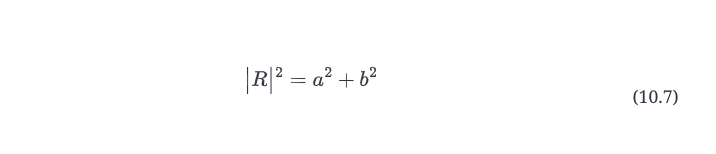
滤波器的频率响应图实际上是一个称为滤波器传递函数的复数函数的幅度响应。相位响应图实际上是这个函数的参数响应。传递函数是复杂的,因为它包含复数;许多传递函数实际上是很简单的。我们用字母H来表示传递函数。传递函数将一个系统的输出与它的输入联系起来(也就是说,它描述了信息从输入到输出的转移)。
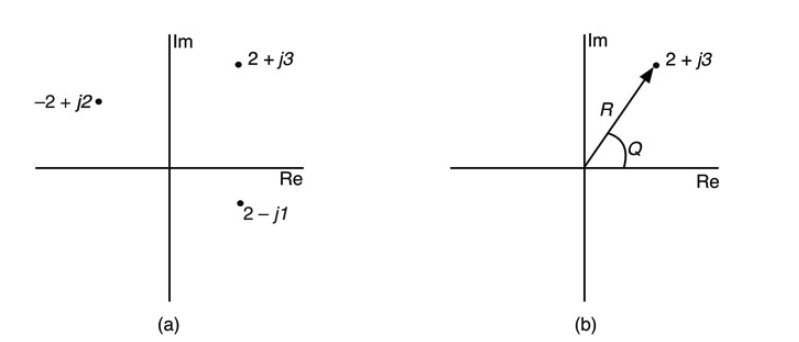
图10.2: 以(a)直角坐标和(b)极坐标形式绘制在复平面内的复数。
方程10.8显示了如何从传递函数中提取幅值和相位;我们很快就会用到这些简单的关系。

10.3 作为数学运算符的时间延时
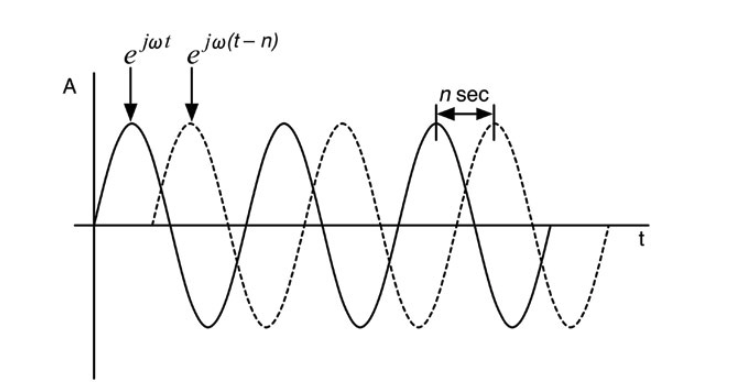
你想了解的下一块DSP理论是作为数学运算符的时间延迟的概念。这将是相当容易的,因为我们要利用e^jωt函数的简单数学行为。首先,考虑一个模拟复数正弦波和同一复数正弦波的延迟版本,如图10.3所示。请注意,这些是模拟波形,X轴上标注的是模拟时间t。
延迟n秒是如何改变复数正弦波方程的?由于正的时间在正的x方向上,延迟n秒就是移位-n秒。在复数正弦方程中,你将用t-n来代替t。换句话说,延迟曲线上的任何一点都与非延迟曲线减去n秒的结果相同。因此,延迟的正弦波是。
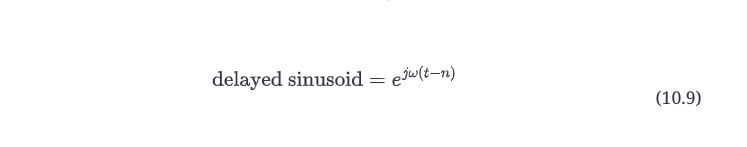
但是,通过使用e的多项式行为和反向运行公式10.5,你可以将其改写为:。
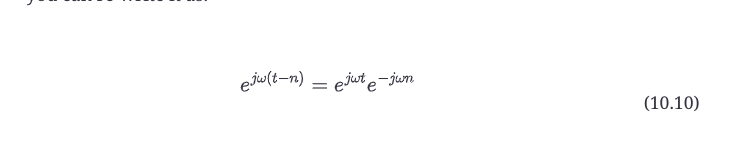
这是一个微妙的数学方程,但它说明了很多问题:如果你想把一个复杂的正弦波延迟n秒,就把它乘以e^(-jωn) 这使我们可以把时间延迟表达为一个数学运算符。
10.4 采样的正弦波
到目前为止,我们一直在讨论的正弦波在技术上是时间t的模拟函数,采样版本只对每个采样间隔T有效。在时间t=0时从0.0开始的正弦波的前几个采样区间将是{0.0μS, 22.7μS, 45.4μS},在图10.4a中可以看到e^(jω0), e^(jω22.7uS)和, e(jω45.4uS)。将采样率减半至22.050kHz,使采样间隔加倍,结果在图10.4b中为e(jω0)、e(jω45.5uS)和,e(jω90.7uS)。
识别采样正弦波的通用方法是用数字化的nT取代模拟时间变量t,其中n是一个计数器,从零开始,每个简单的间隔都向上计数,T是采样周期。然后,正常的和延迟的版本将由样本而不是连续的模拟时间来联系。对于延迟的M个样本,我们可以这样写。

因此,如果你想把一个数字化的复数正弦波延迟M个样本,就把它乘以e^(-jωM)。
时间延迟可以表示为一个数学运算符,即用模拟信号延迟n秒乘以e(-jωn)。对于要延迟M个样本的数字化信号,你要乘以e(-jωM)。这很有用,因为e(-jωn)和e(-jωM) 都不依赖于时间变量t或nT。
在上两节中,你已经了解到相位旋转和时间延迟都可以用数学运算符表示。
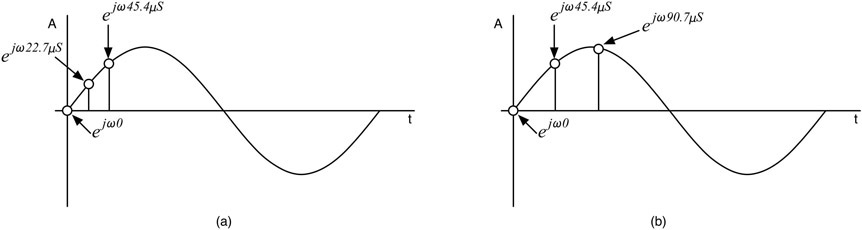
图10.4:(a)fs = 44.1 kHz和(b)fs = 22.050 kHz的正弦波的前三个样本。
10.5 重温一阶前馈滤波器
能够用e^(-jωM)相乘的数学运算来表达M个样本的延迟,意味着你可以用DSP滤波器的框图和差分方程,以 e^(jωnT) 的形式将正弦波应用于输入,而不必像第二章那样插入样本的序列。然后,你就可以看到滤波器的数学表达式,并对不同的ω值(其中ω=2πf,f为Hz)进行评估,直接找到频率和相位响应,而不是等着看出来的东西,然后再去猜测振幅和相位偏移。考虑一下上一章中的一阶前馈滤波器,但将e(jωnT)作为输入信号,如图10.5所示。在这种情况下,z-1状态寄存器可以用e(-jω1)的乘法来代替,以实现单样本的延迟元件。
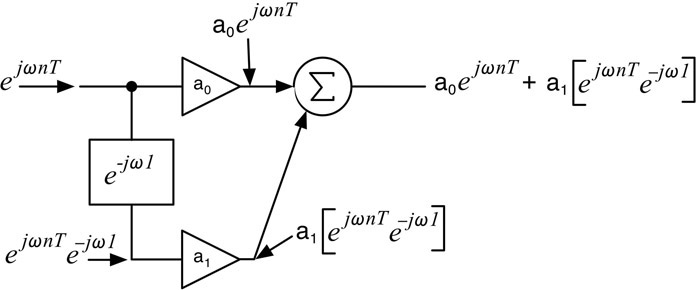
图10.5:一阶前馈滤波器的输入为复数采样的正弦波。
应用e^(jωnT) 作为输入信号的不同方程是:
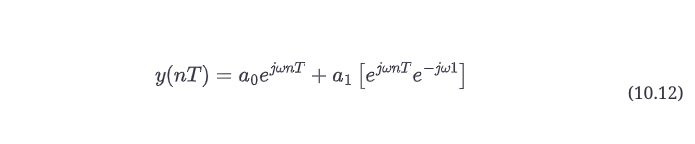
现在我们可以通过分离原始输入x(nT)和新形成的输出y(nT)来执行一个(几乎)惊人的数学小特技。
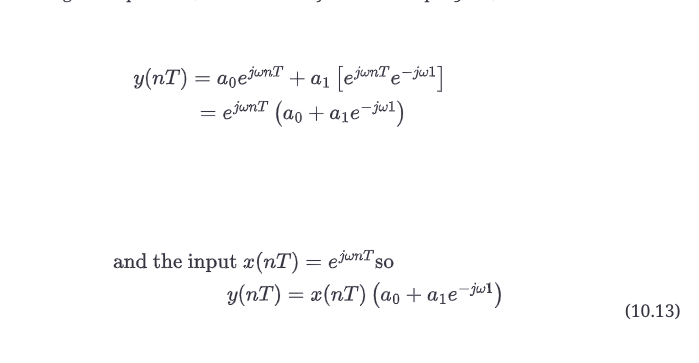
传递函数被定义为输出与输入的比率,因此
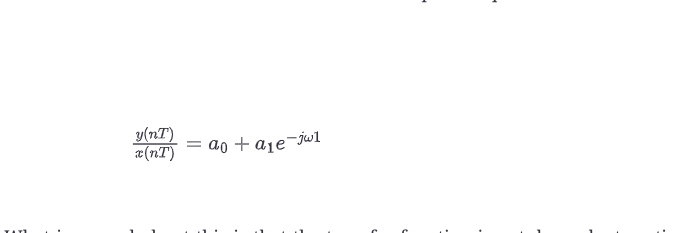
这其中最酷的是传递函数不依赖于时间nT,尽管输入和输出信号是时间的函数。事实上,传递函数只依赖于频率ω。这意味着我们可以重写传递函数,将其称为H(ω)。有些工程师喜欢把传递函数记为依赖于复数频率,或jω,他们会把传递函数写成H(jω)。在这里,我们将坚持使用更简单的术语,只叫它H(ω)。
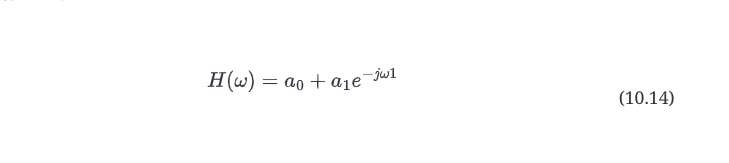
滤波器的传递函数是输出与输入的比率。
滤波器的频率响应是传递函数的大小。
滤波器的相位响应是传递函数的argument (或角度)。
为了制作频率和相位响应图,你要对函数进行评估,以确定ω的不同值,然后找出每个频率的幅度和参数。
评估总是使用欧拉方程来替换e项,并产生实部和虚部,然后可以用公式10.8将其转换为幅值和参数。
但是,在评估中要使用什么数值的ω?我们知道ω=2πf,但我们真的关心频率(Hz)吗?在第二章中,当你分析同一个滤波器时,你应用了DC、Nyquist、1/2 Nyquist和1/4 Nyquist,而没有考虑到实际的采样频率。这被称为使用归一化的频率,通常是你在分析DSP滤波器时想采用的方式。实际的采样率决定了奈奎斯特,但整个频率范围(0Hz到奈奎斯特)才是我们关心的。为了使频率正常化,你让f = 1 Hz的ω = 2πf,然后ω从0到2π或在2π的范围内变化。还有一个我们需要注意的细节:负频率。
10.5.1 负的频率
你可能从未想过频率可以是负的,但它可以。当你第一次学习波形频率的概念时,你被告知,频率是1/T,其中T是周期,如图10.6a所示。频率之所以是正数,是因为周期被定义为t2-t1,使其成为一个正数。但是,你没有理由不把周期定义为相反的方式。T = t1- t2(除了这意味着时间在倒退)。在数学上,时间可以倒流。这意味着每一个正的频率存在,也有一个负的 "孪生 "频率。当你看一个频率响应图时,你一般只看正的一面。图10.6b显示了一个教科书式的低通响应,直到系统的最高频率。奈奎斯特。注意,频率响应显示的是传递函数的大小,|H(f)|。
在现实中,滤波器也是在负的频率上工作,就像镜像一样。在这种情况下,随着负的频率越来越高,它们会像图10.7a中的正的频率一样被衰减,而且这也是有意义的。如果你把一个音频文件在时间上倒过来,然后通过一个低通滤波器,同样的频率过滤仍然发生。对于滤波器的评估,ω在0到2π弧度/秒的范围内变化;思考这个2π范围的一个方法是把它分成从-π到+π的范围,对应于-Nyquist到+Nyquist,如图10.7b。
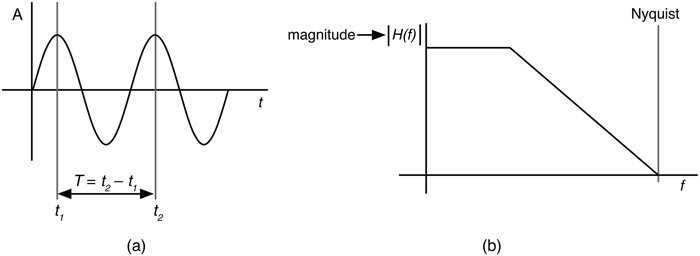
图10.6:(a)经典的 "教科书 "定义的周期迫使产生的频率总是一个正值,如图所示。(b) 显示频率响应图的常见方法是只显示正的频率,即右侧。
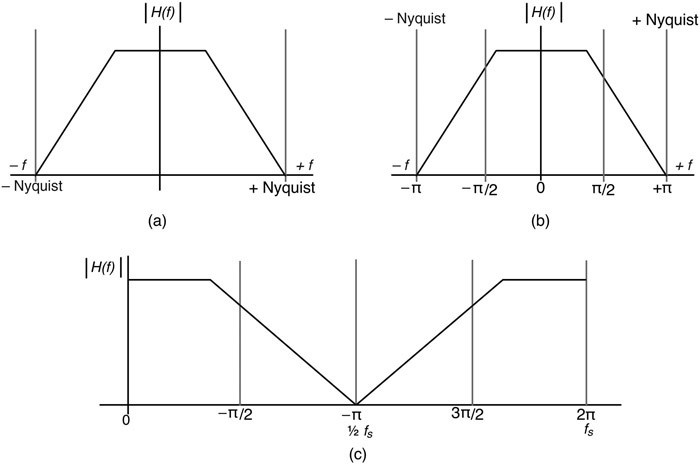
图10.7:(a)这里显示的更完整的频率响应图包含了正负两个频率。(b) 一种划分频率2π的方法包括正负两半。(c) 我们也可以将0到2π的频率映射到0到fs的范围内。
采样定理设定了奈奎斯特标准,涉及到完全恢复原始的、带限制的信号和无混叠。但是,高于奈奎斯特的频率和一直到采样频率fs的频率在数学上也是允许的--理论上,任何频率都可以进入系统,你可以对它进行采样而不限制最大频率分量到奈奎斯特。对于一个频率或相位响应图,从奈奎斯特到采样频率的频率是关于奈奎斯特的镜像。这是另一种方法,从0Hz到采样频率的2π范围划分,如图10.8c所示。请注意,在这两种方法中,传达的信息是相同的,因为我们得到了两半的曲线,在这两种情况下,奈奎斯特映射到π,0 Hz映射到0,正频率映射到0到π的范围。
为了评估传递函数,让ω从0到π变化,得到响应的前一半。另一半则是数据的镜像。
10.6 评估传递函数H(ω)
DSP滤波器的传递函数将包含e^(˗jωn)项,需要在0到π的范围内进行评估。方法是使用欧拉方程将正弦波分解成实部(cos)和虚部(sin)。然后,在评估的频率上评估cos和sin项。在第9章中,我们通过一步一步地计算滤波器的输入/输出关系:我们做了四次,对每个输入频率ω做一次。让我们从图10.6的框图开始,我们的老朋友一阶前馈结构和它的传递函数。
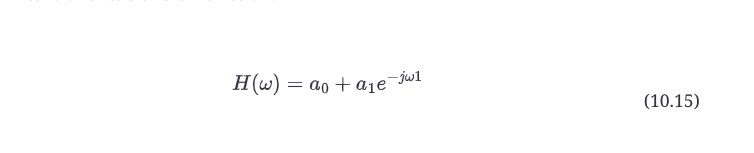
我们将使用系数a0=0.5和a1=0.5,我们将在与第二章相同的频率下评估传递函数,只是这一次我们将使用我们基于π的等价物来表示采样率的各种分数。我们可以预先计算sin和cos项,并创建表10.1以使操作更简单。
对每个频率的评估是一个两步的过程。
- 使用欧拉方程将e项转换为实部和虚部。
- 在每个评估频率下找到复数方程的模和夹角。
在每种情况下,我们将把得到的结果与第二章的图形结果进行比较,这些结果浓缩在图10.8中。
表10.1: 在0和Nyquist之间的频率上的各种sin和cos的评价
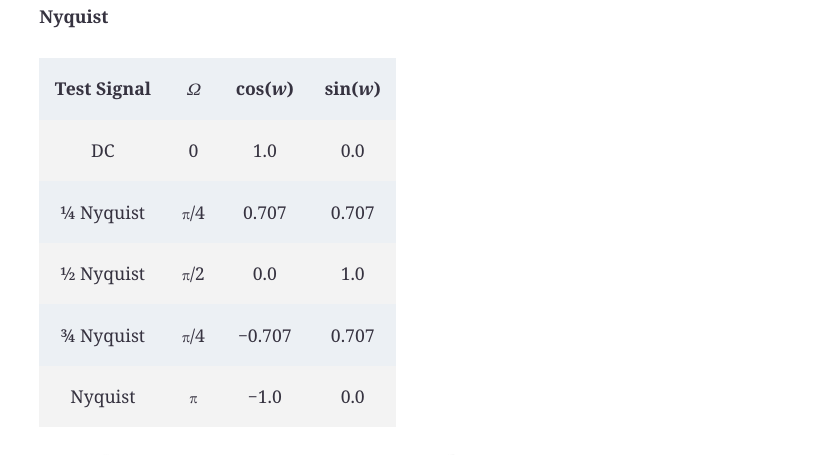
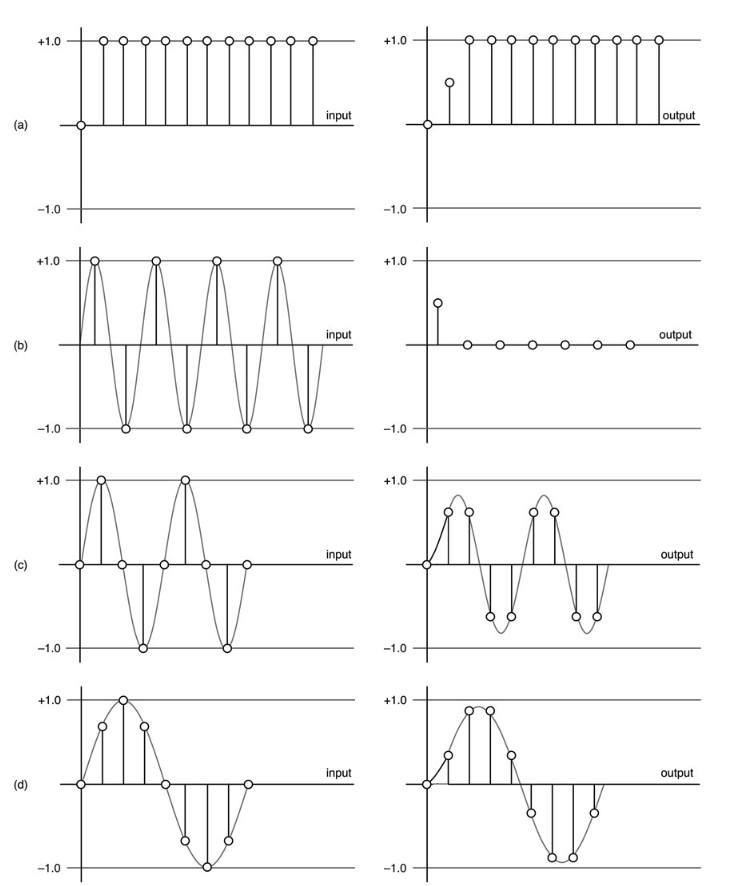
图10.8:我们在第二章中对一阶前馈结构的分析得到的图形结果:(a)直流(0 Hz),(b)奈奎斯特,(c)½奈奎斯特,和(d)¼奈奎斯特。
10.6.1 直流 (0 Hz)
首先我们对e项应用欧拉方程,然后用公式10.6和10.8求出幅值和相位。
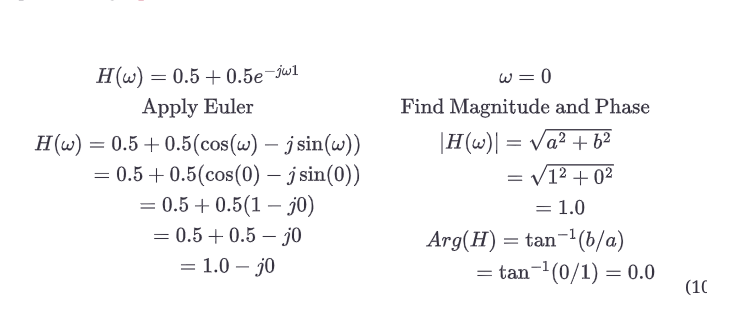
现在将这些数学结果与上一章的结果进行比较,如图10.8a。我们观察到的滤波器在直流时的幅值响应是统一增益(输出=输入),相位偏移为0度(这可以说是无足轻重的,因为直流波形是没有相位的)。现在,让我们对奈奎斯特频率重复这一过程,并与图10.8中的观察结果进行比较。
10.6.2 奈奎斯特(π)
重复ω=π时的评估程序。
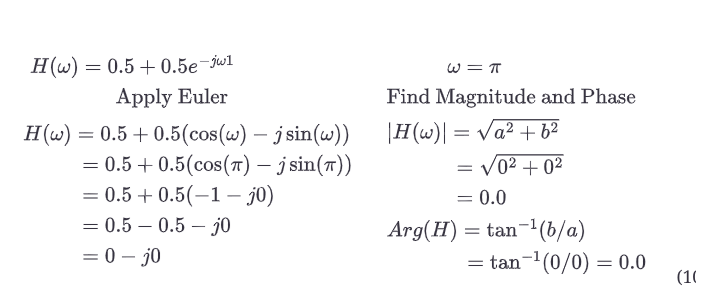
反正切参数是0/0,相位或Arg(H)在这个条件下被定义为零。你使用的C++函数是arctan2(im, re),它执行的是反正切函数;在这种情况下它的值也是0。现在,将我们的结果与上一章的图形结果相比较,如图10.8b所示。再一次,我们得到了相同的结果;相移同样可以忽略不计,因为没有频率分量需要转移,因为它的幅度是0.0。
10.6.3 ½ Nyquist (π/2)
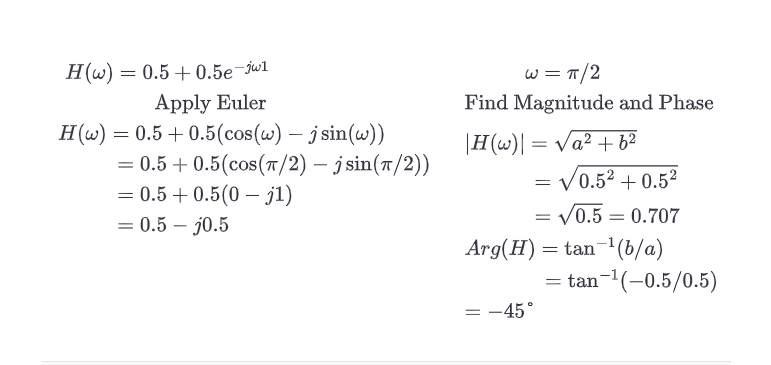
将这个结果与上一章的图示结果进行比较,图10.8c;幅度为0.707,相移为-45度:结果再次一致。由于0.707=-3dB,这也意味着我们已经找到了滤波器的截止频率或-3dB频率,fc= ½ Nyquist。
10.6.4 ¼ Nyquist (π/4)

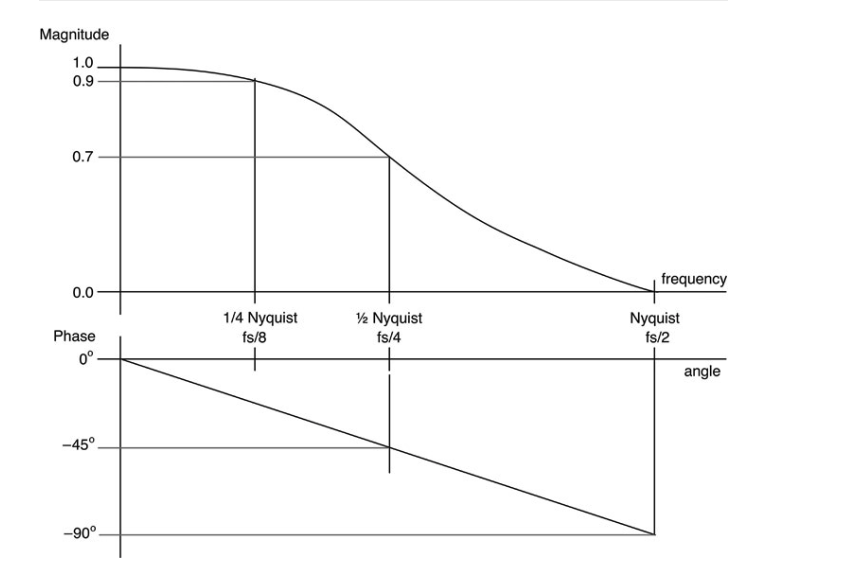
图10.9: 我们预测的频率和相位响应图显示了与第二章相同的结果,但少了很多繁琐的东西。
与图10.8c相比,你可以看到我们用数学计算得到的精确度要高得多。与图相比,幅值和相移看起来差不多。现在,你可以把所有的评估结果结合起来,在图10.9中勾勒出滤波器的频率响应--看,这和我们在第二章中得到的结果一样,但更准确。希望这个简单的例子能让你相信,与其通过对时域输入序列的粗暴分析来分析和设计这些滤波器,不如做一点复杂的数学运算。
10.7 评估e^(jω)
在评估传递函数时,你必须将ω的值从0到π代入方程中的e^(jω)项。但是,如果你单独评估一个 e^(jω) 项,图会是什么样子?你看到了使用欧拉方程产生了项的实部和虚部;现在是时候在0到π的范围内绘制它们了。如果你在更多的频率上评估 e^(jω) ,并将结果值绘制在复平面上,你会得到一个有趣的结果:表10.2中从0到+π的频率映射到一个圆的上半部分,半径=1.0,如图10.10a。记住,使用极坐标符号时,幅度是半径,参数是角度,这就简化了分析。你不需要跟踪实部和虚部。在ω=π/4处的评价被画在曲线上。这个弧线所在的圆的半径为1.0,被称为单位圆。如果你在对应于0到-π的负频率上评估 e^(jω) ,你会得到一个类似但颠倒的表格(表10.3),转化为横跨同一单位圆下半部分的映射,如图10.10b所示。负的频率随着你从0Hz顺时针移动而增加,而半径在整个弧线上保持1.0。
为什么要费心评估 e^(jω) 呢?当我们开始挑剔传递函数,努力找出如何设计滤波器时,它很快就会有用。它还显示了数字域的有限 "频率空间"。从-Nyquist到+Nyquist,所有可能存在的频率都映射到一个简单的单位圆。在合同中,模拟域有一个无限长的频率轴和一个无限大的频率空间。
10.8 z替代法
经常写e^(jω) 会变得很乱,而且我们知道 e^(jω) 在数学上的表现和多项式一样。因此,我们可以通过对公式10.20进行简单的替换来简化方程。
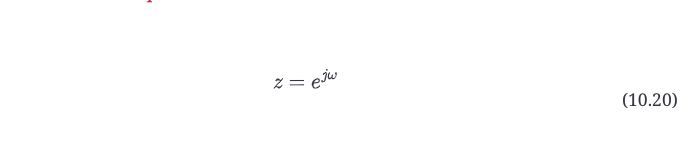
现在这只是一个代换,没有别的意思。在公式10.20中进行替换,并注意到所得到的传递函数现在是z的函数,而不是ω,我们可以这样写。
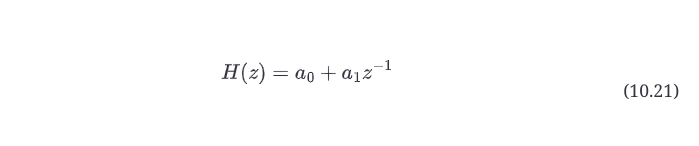
在这种情况下,这个多项式是一阶多项式(最高的指数绝对值是1),这就是滤波器被称为一阶滤波器的真正原因--它是传递函数的多项式阶数。
表10.2:从直流到奈奎斯特的e^(jω)的大小和角度
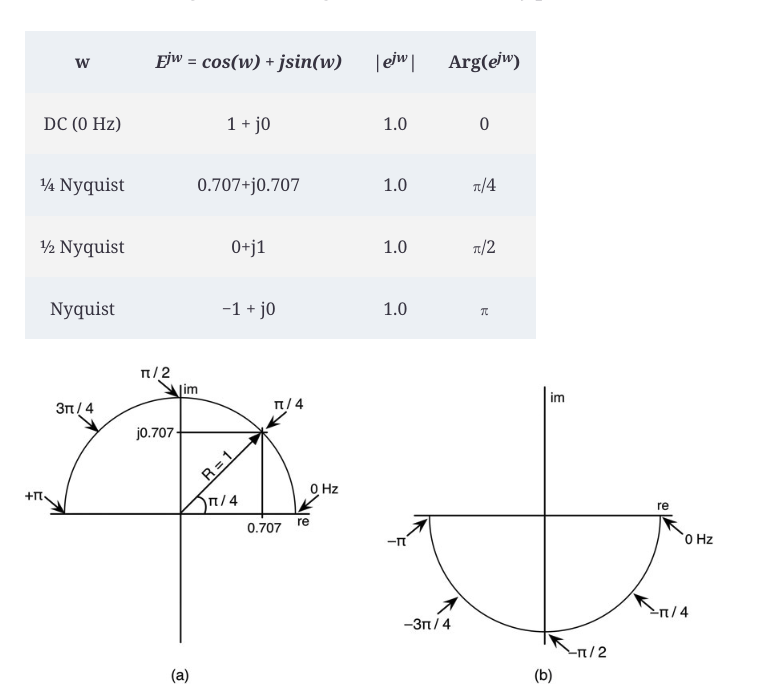
图10.10:(a)正频率映射到单位圆的上半部分。(b) 负的频率映射到下半部分。
表10.3:从DC到-Nyquist的eJw的大小和角度
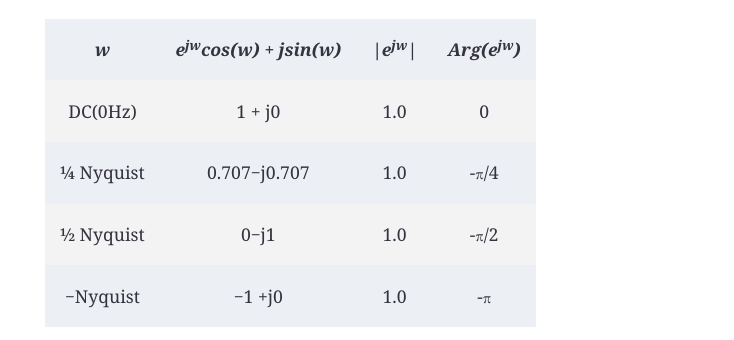
滤波器的阶数是描述它的传递函数的多项式的阶数。多项式的阶数是方程中发现的最大绝对指数值。
10.9 z变换
z置换在简化ejω的基本多项式行为方面做得很好,它让我们使用多项式数学来解决DSP问题。但z = ejω有一个有趣的应用,它简化了数字滤波器的设计和分析。在图10.11中,你可以看到样本的索引如何决定它们在时间上的位置。未来的样本有正的索引,过去的(延迟的)样本有负的索引。
我们已经看到e˗jω是延迟算子,所以e˗jω1意味着延迟一个样本,或比当前样本晚一个样本。同样,e˗jω2将是落后两个样本,e+jω4表示领先四个样本或未来。这意味着,ejω也可以作为一种记账工具,因为它可以将某物(对我们来说是一个样本)在时间上的位置联系起来
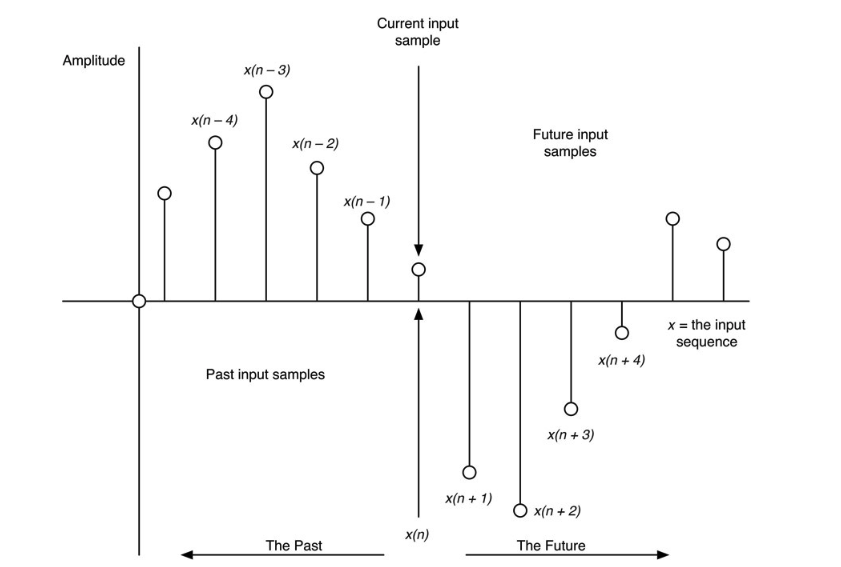
图10.11:我们的音频样本记账规则以图形显示。
z变换将n中的样本序列改变为z中的样本序列,将指数...n-1, n, n+1...替换为...z-1, z, z+1...这是因为乘以z=ejω代表延迟或时移的操作。
现在产生的转换序列是复数频率ejω的函数,因此它将事物从时域转换到复数频率域。
在离散信号或差分方程上实现z变换的规则很简单,通常可以通过检查来遵循。当前样本x(n)或y(n)转换为信号X(z)或Y(z)。与其考虑样本x(n),不如考虑信号X(z),其中X(z)是整个信号--过去、现在和未来。
x(n) à X(z)
y(n) à Y(z)
与其认为样本x(n - 1)被延迟了一个样本,不如认为信号X(z)被延迟了一个样本,即z-1。延迟的信号是整个信号乘以z-N项的结果。
x(n - 1) à X(z) z-1
y(n - 1) à Y(z) z-1
x(n - 2) à X(z) z-2
y(n + 6) à Y(z) z+6
你可以看到,这个概念依赖于将延迟表达为一个数学运算符的能力。它不仅允许我们基于z来表达一个算法,而且还让我们基于z来表达一个信号。在数学上,z变换是。
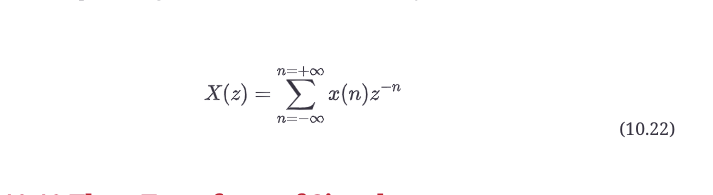
10.10 信号的Z变换
记住,方程10.22中的x(n)是一个样本序列,就像你用于分析的那些样本一样。图10.12a显示了一个例子。
这个简单的、有限长度的信号由五个样本组成。
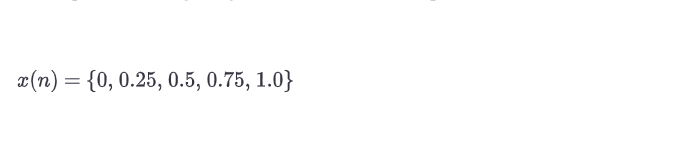
剩下的零样本不需要计算。序列x(n)也可以写成x(n)={x(0), x(1), x(2), x(3), x(4)},所以用公式10.22我们可以把信号的z变换写成。
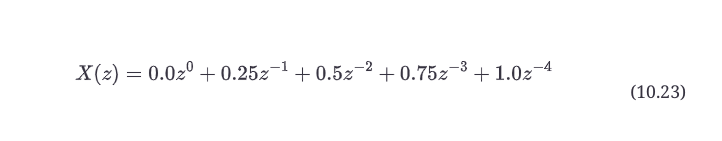
你可以这样解读方程10.23。
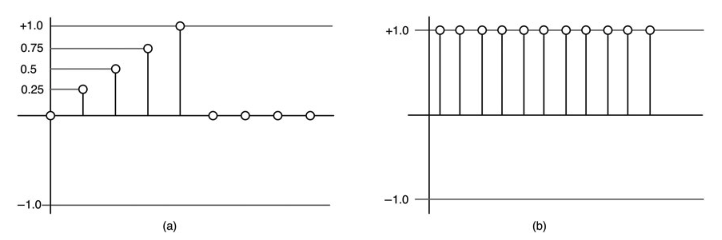
图10.12:Z变换的两个信号:(a)一个由5个样本组成的有限ramp-burst,(b)一个由所有1.0值样本组成的无限直流序列。
整个信号,X(z)包括一个在时间0时振幅为0.0的样本,然后是一个样本后振幅为0.25的样本,两个样本后振幅为0.5的样本,三个样本后振幅为0.75的样本,四个样本后振幅为1.0。这应该说明了一个事实,即转换实际上涉及到样本在时间上的位置的记账,其结果是一个多项式。你可以通过使用多项式数学将这个信号与其他信号相乘或相除。你可以通过线性组合多项式来混合两个信号。
让我们再做一个关于输入信号变换的例子。这一次,让我们选择直流信号--它一直在持续。图10.12b显示了直流信号,第一个样本在1.0,所有前面的样本在0.0,序列为x(n) = {1.0, 1.0, 1.0, 1.0, 1.0 ...}。使用公式10.22(并记住1z0=1),我们可以直接将z变换写成。
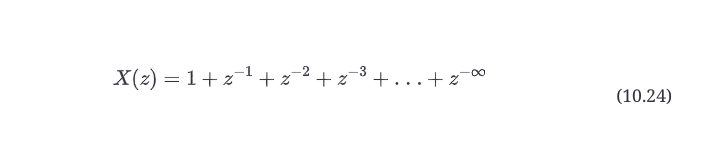
虽然这看起来是一个丑陋的、无限长的方程,但它也可以用封闭形式表示。事实上,这个多项式存在一个使用多项式级数展开的封闭形式表示。
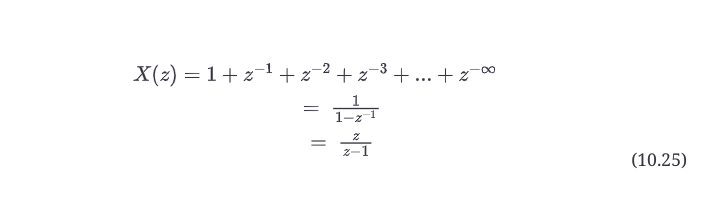
10.11 差分方程的z变换
信号的z变换很有意思,但是当你把差分方程的z变换,一下子转换成z中的传递函数时,就会发生一些奇妙的事情--同样的简单规则也适用。让我们用基本的一阶前馈滤波器来做这件事。

这是一个非常有趣的结果--你只用了几步就得到了最终的传递函数,使用的是简单的z变换规则。让我们回顾一下,在你学会如何进行差分方程的z变换之前,你必须做什么。
用e-jωn运算符在n个采样延迟元素中重新绘制框图。
将复数正弦波e-jωnT应用于输入。
找出结果,y(nT),并制定传递函数H(ω)。
对传递函数应用z置换法。
如果我们对z = ejω的不同值评估传递函数,我们可以找到频率和相位图。你很快就会得到更多关于更多差分方程的z变换的练习。
10.12 脉冲响应的z变换
对一个差分方程进行z变换的结果是传递函数。但如果你没有差分方程呢?假设你只有一个执行某种DSP算法的黑盒子,你想弄清传递函数,评估它,并绘制频率和相位响应。在许多情况下,这可以在不知道算法或关于它的任何细节的情况下通过获取系统的脉冲响应来完成。你应用输入序列x(n)={1,0,0,0,0 ...},并捕捉到产生的东西,我们称之为h(n)。如果你采取脉冲响应的z变换,你会得到扩展为序列形式的传递函数。
脉冲响应h(n)的z变换是传递函数H(z)的序列展开。对传递函数进行评估,绘制出频率和相位响应。
事实上,这正是RackAFX软件的音频分析器所做的:它获取滤波器的脉冲响应,然后对其进行z变换,绘制出你在屏幕上看到的幅值和相位图。在数学上,公式10.27与公式10.22相同,只是我把信号从X改为H。
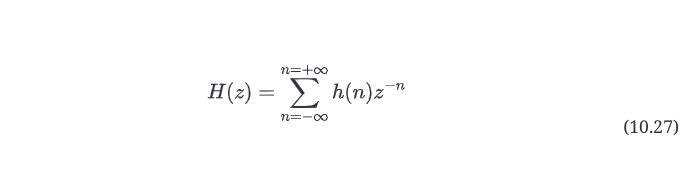
在我们一直在研究的一阶前馈滤波器上试试这个方法;你已经在图10.13中 "捕获 "了上一章的脉冲响应。脉冲响应是
h(n) = {0.5, 0.5}。
应用z变换可以得到。
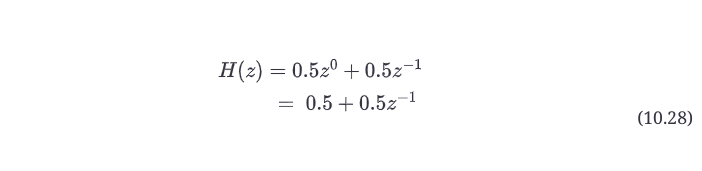
请注意,这与取差分方程的z变换结果相同,滤波器系数(0.5,0.5)是脉冲响应{0.5,0.5}。
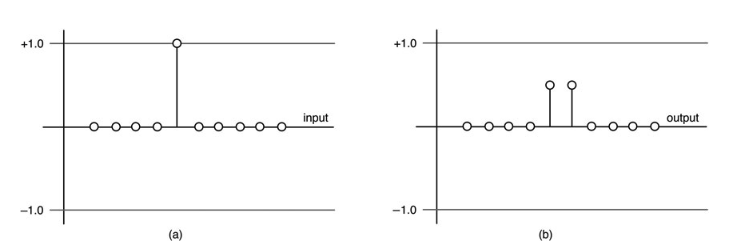
图10.13:第二章的一阶前馈滤波器的脉冲响应输入(a)和输出(b)。
10.13 传递函数的零点
当我们在一阶前馈结构中使用系数a0 = a1 = 0.5时,我们得到了一个完全破坏了奈奎斯特频率的滤波器--你看到它的输出在手工计算和复数正弦的评估中都变成了0。我们注意到,前馈滤波器在其输出变为0时,有传输零点或零频率(或只是零点)。在手工计算和复数正弦波的评估中,我们只是幸运地偶然发现了这个值,因为奈奎斯特刚好是我们评估的信号之一。有一种方法可以通过使用z变换的多项式结果精确找到这些临界频率。你可能还记得高中或大学时的多项式因式分解。当你这样做的时候,你把多项式设为0,然后你通过因式分解来找到多项式的根。你真正在做的是寻找多项式的零点,也就是使多项式变成零的自变量的值。你可以对转移函数做同样的事情,把它设为零,然后对多项式进行因式分解。假设a0 = a1 = 0.5,我们对方程10.28中的传递函数进行因式分解,得出以下变化。
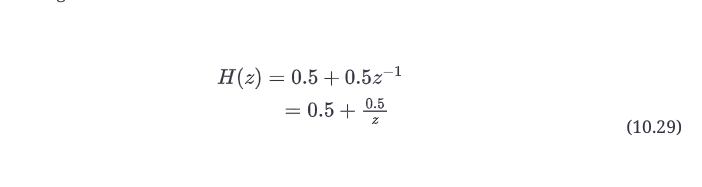
你可以通过检查找到零点:它是迫使H(z)为0的z值。在这种情况下,我们说 "在z=-1.0有一个零点"。但是在-1.0处有一个零点到底意味着什么?这就是评估ejω的概念发挥作用的地方。当你这样做并绘制各点时,注意到它们在复平面上形成一个单位圆,你实际上是在z平面(即ejω的平面)上工作。z=-1.0处的零点位置实际上是在z=-1.0+j0处,而且纯粹是在实轴上和奈奎斯特处。在图10.14中,零点被显示为一个位于z = -1.0位置的小圆。
绘制零点频率有几个原因。首先,你可以直接在Z平面上设计某些滤波器,首先决定你要把零点频率放在哪里,然后找出能给你这些零点的传递函数。其次,绘制零点可以让你快速勾勒出频率响应,而不必直接评估传递函数。你也可以估计一个相位图,但这是一个有点复杂的问题。因此,你有两个真正好的理由想要绘制零点:一个用于设计,另一个用于分析。
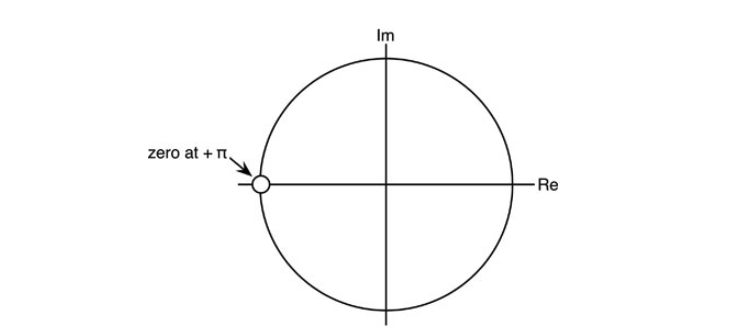
图10.14:零点在z平面上被绘制成一个位于z=-1+j0的小填充圆。
10.14 估计频率响应。零点
z平面和z变换的一个有趣的特性是,你可以在z平面上用图形测量频率响应。在只有一个零点的最简单情况下,方法如下。
在单位圆的外缘找到每个评估频率。
从圆上的点到零点画一条线,测量这个向量的长度。对每个评价频率都这样做。
线的长度将是频率响应中每个频率的振幅。
在图10.15中,你可以看到完整的操作:首先画线和测量线(如果你愿意,可以用图画纸和尺子),然后根据它们建立频率响应图。还要注意的是,从奈奎斯特到-1的零点所画的线的幅值的长度为零。向量的长度是数学上对不同评估频率下的幅度的定义;你是在一次评估整个滤波器。这些Z平面图对滤波器的设计会很有帮助。你也可以推导出相位响应,但这比较繁琐,需要将每个向量在零点上的入射角相加。如果有多个零点,就会变得很麻烦--但是估计频率响应是相当简单的,即使是对比较复杂的滤波器也是如此。
你可能会注意到,尽管这个频率响应看起来像我们之前制作的那个,但是增益值却不一样。在这个滤波器中,直流时的增益是2.0;而在我们的滤波器中,它是这个值的一半。事实上,这个滤波器在评估频率上的幅度都是我们的两倍。在下一节,我们将看到原因。
10.15 滤波器增益的控制
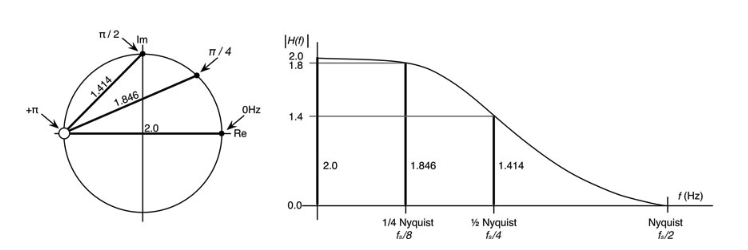
图10.15:几何方法显示了从评估频率到零点的每个向量的长度实际上是最终响应中的一个幅度。
我们需要做的最后一件事是从传递函数中去掉整体增益因子,这样整个滤波器的增益(或衰减)就可以由一个变量控制。这实际上是相当简单的,但需要对传递函数进行一些重新的处理。我们的想法是将a0变量作为整个函数的乘法器拉出来。这样一来,它就像一个音量旋钮,将整个滤波器向上或向下增益。你的方法是通过除掉a0来使滤波器正常化,如下所示。
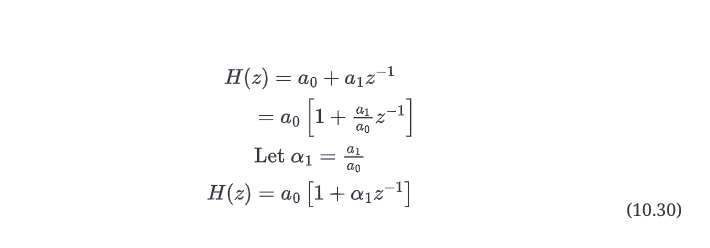
通过去掉a0系数并使用α1术语,我们可以产生一个传递函数,该函数在多项式中看起来基本相同,但将a0拉出来作为一个标量乘数--增益控制。
这个新传递函数的零点在哪里?
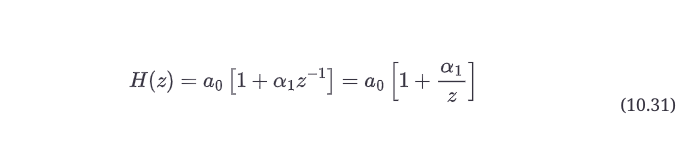
再次,通过检查公式10.31我们可以看到,如果z=-α1,那么无论a0的值是多少,函数都会变成0。这个传递函数在z=-α1处有一个零。如果我们把a0 = a1 = 0.5的值插入,我们仍然可以在z = -1.0处得到相同的零。区别在于滤波器的增益。
在Z平面上评估滤波器的图形解释方法假定滤波器被归一化,所以a0=1.0。
因此,在从z平面图中提取幅度响应后,你需要做的最后一步是将其按a0值进行缩放。这使得图10.24中的响应与我们的一致,因为所有东西都被乘以a0 = 0.5。独立于幅度响应来控制增益的想法在音频滤波器中很有用,所以我们将保留它,并在所有进一步的分析中使用它。
到此为止,你已经拥有了理解其余经典DSP滤波器(一阶反馈、二阶前馈和反馈)所需的所有DSP理论工具,以及许多滤波器设计技术。本章的其余部分将致力于将这些相同的基础知识应用于其他经典DSP滤波器--但我们将更快地推进,将每一种分析技术应用于其他算法。例如,我们将省去对ejω项的评估,直接从差分方程的z变换开始。
10.16 重温一阶反馈滤波器
现在让我们对上一章中的一阶反馈滤波器进行同样的分析技术。既然我们已经掌握了基本的DSP理论,我们就可以更快地进行分析。在处理反馈设计时,会有许多相似之处,但也有几个关键的区别。你已经看到,反馈拓扑结构可以炸毁或永远响起,而前馈设计则不能。我们将找到一种方法来弄清楚这是否会发生,以及如何防止它。从图10.16a中的原始一阶反馈滤波器和它的差分方程开始。
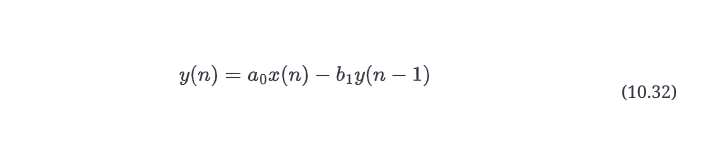
10.16.1 步骤1:取差分方程的z变换
这可以使用第10.9节的规则通过检查来完成,也可以通过将转换后的输入X(z)推过图10.16b所示的结构,注意到中间节点,并找到结果Y(z)。使用这两种方法,差分方程的z变换都是。
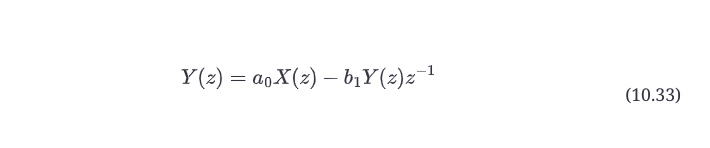
请注意,当我们将输入样本x(n)通过滤波器推到形成输出样本y(n)时,通过延迟寄存器的移动将索引从n变为n-1,但是当将整个输入信号X(z)通过滤波器处理成Y(z)时,通过延迟寄存器的移动将其乘以z^-1。然后,我们可以很容易地得到z的差分方程。
10.16.2 第二步:将差分方程转变为传递函数
现在应用一些代数来将转换后的差分方程转换为H(z)。这个过程总是相同的:分离X(z)和Y(z)变量,然后形成它们的商。
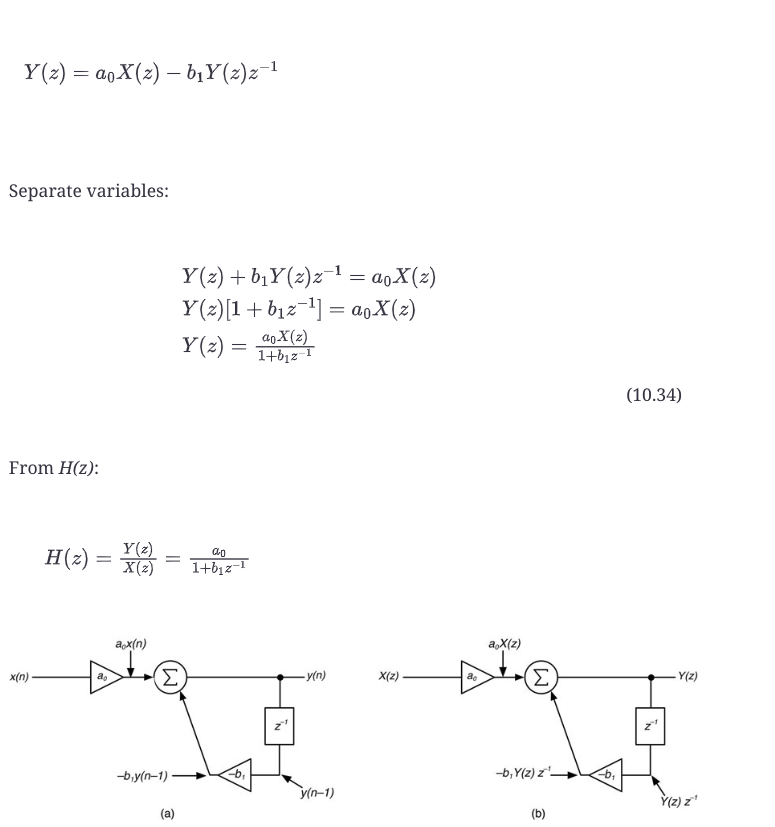
图10.16:(a)通过一阶反馈结构处理样本x(n),(b)通过滤波器处理输入X(z),我们可以很容易地找到其z变换。
10.16.3 第3步:将a0作为标量增益系数的因子拉出来
在这种情况下,这一步很简单,因为把a0拉出来是很容易的。然而,在更复杂的滤波器中,这需要像我们在上一节所做的那样进行替换。
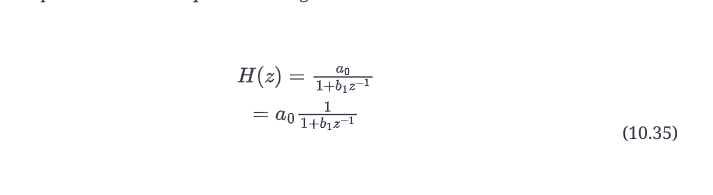
10.17 传递函数的两极
接下来的步骤是用图形解释法在Z平面上对频率响应做一个快速估计。我们分析的纯前馈滤波器在其输出变为零的频率上产生传输的零点或零点。纯反馈滤波器在其输出变成无限的频率上产生极点。在上一章中,我们通过应用100%的反馈来实现这一目的。对于简单的一阶情况,找到极点可以通过检查来完成。
当传递函数的分母为零时,输出是无限的。发生这种情况的复杂频率就是极点频率或极点。
检查传递函数,我们可以在公式10.36中找到单极。
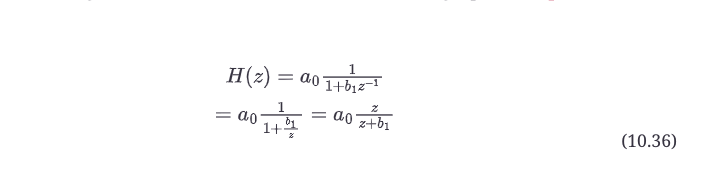
通过重新排列传递函数,你可以看到,当z=-b1时,分母将为零,所以在z=-b1处有一个极点。你可能还注意到这个传递函数的一些有趣的地方:它的分子中有一个z。如果z=0,那么这个传递函数在z=0处有一个零点。这个零点被称为微不足道的零点,因为它对滤波器的性能(频率响应)没有影响。所以,你可以忽略z = 0处的零点。事实上,出于同样的原因,你也可以忽略z = 0处的极点。
z=0处的极点或零点是微不足道的,为了分析的需要可以忽略,因为它对频率响应没有影响。
如果你回头看看前馈滤波器的传递函数,你可以看到它在公式10.37中也有一个微不足道的极点。
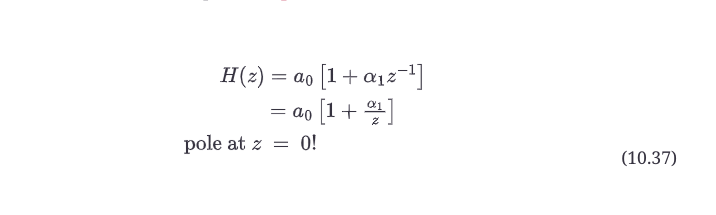
极点以与零点相同的方式绘制在z平面上,但你用x来表示极点频率。在一阶反馈的情况下,极点在-b1+j0,所以它是一个位于z面实轴上的实极。对于这个滤波器,我们用a0 = 1.0和b1 = 0.9来分析。这个滤波器的测量频率响应如图10.17a所示。让我们先看看这是如何估计的,然后我们就可以像以前一样进行直接评估。
10.17.1 第四步:估计频率响应
在实轴上的单极绘制在z = -0.9 + j0处,在z = 0 + j0处有一个琐碎的零点。这在图10.17b中显示。在未来,我们将忽略琐碎的零点或极点。
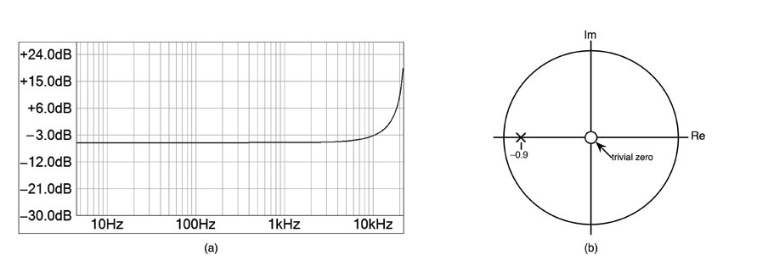
图10.17:(a)一阶反馈结构的测量频率响应,fs = 44.1 kHz,a0 = 1.0,b1 = 0.9。(b)算法的极点/零点图。
在只有一个极点的最简单情况下,估计频率响应的方法如下。
将每个评估频率定位在单位圆的外缘。
从圆上的点到极点画一条线,测量这个向量的长度。对每个评估频率都这样做。
线的长度的倒数将是频率响应中每个频率的幅度,如公式10.38所示。

因此,其机制与一零情况相同,只是你采取了矢量长度的逆数。这意味着,当你接近极点时,矢量会变短,但幅度会变大--与零的情况完全相反。四个评估频率及其矢量显示在图10.18a中,我们预测的频率响应显示在图10.18b中。请注意,奈奎斯特的增益是10.0:换算成dB,你会得到+20dB的增益,这就是我们在图10.19a中观察到的测量响应。
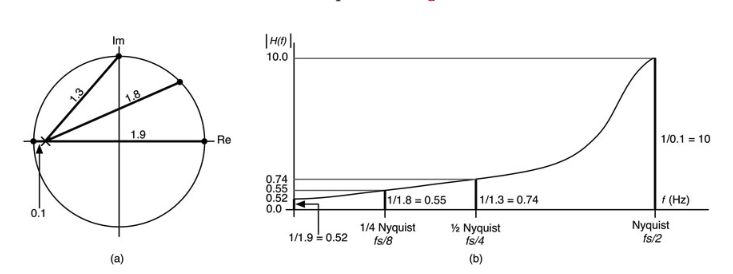
图10.18:(a)极点/零点图的图形评估。(b) 我们的一阶反馈滤波器的估计频率响应。
10.17.2 第五步:对频率响应进行直接评估
现在我们可以用之前的方法来评估滤波器,用欧拉方程来分离传递函数中的实部和虚部。
在以下频率进行评估。
直流:0
奈奎斯特:π
1/2 奈奎斯特:π/2
¼ 奈奎斯特:π/4
首先,在方程10.39中得到用于所有评估频率的传递函数。还要注意ejω--这就是欧拉方程将发挥作用的地方。


10.17.6 ¼ Nyquist (π/4)
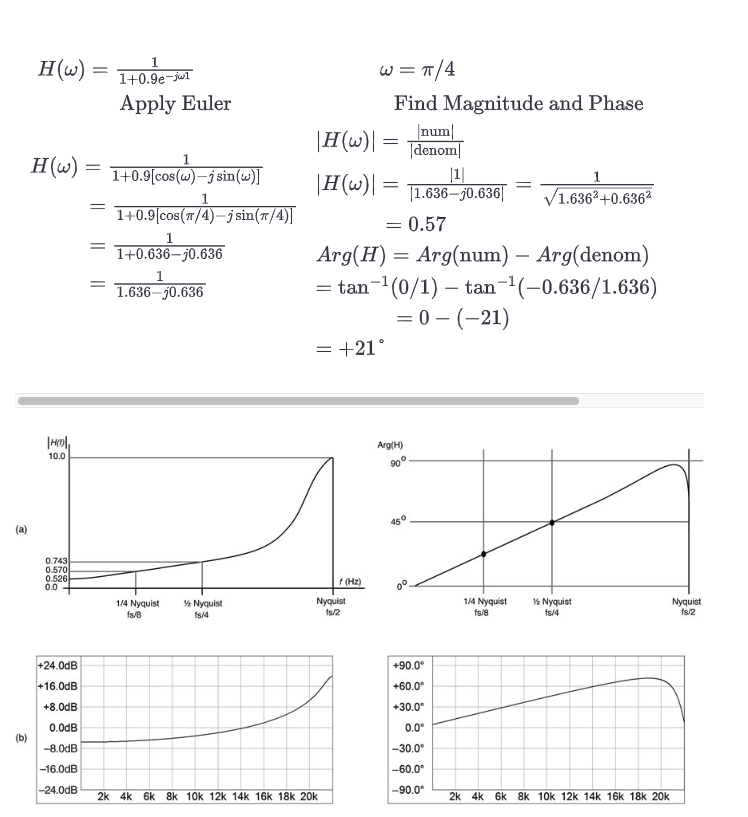
图10.19 (a) 一阶反馈滤波器的计算频率响应(左)和相位响应(右)。(b) 滤波器的测量频率响应(左)和相位响应(右),fs = 44.1 kHz。注意,测量的频率响应幅度是以dB为单位,而计算的响应是以原始值为单位。
请特别注意,我们要如何处理有分子和分母的分数的大小。你需要使用[10.8]中的两个方程式来处理这个问题。主要的问题是,相位是Arg(分子)和Arg(分母)的差。如果分子是一个复数而不是1.0,我们就需要分别取其大小,然后进行除法。图10.19a和b显示了计算和测量的响应图。你可以看到,相位的表现是线性的,直到它接近极点,然后表现为非线性。这不是一个线性相位滤波器。在图10.19中,我们观察到与我们的评估非常一致:响应在直流(0.52)时下降了-6dB,在奈奎斯特(10)时下降了+20dB,相位在π/2时是45度。
我们在直接评估这个滤波器时遵循五个步骤。
取差分方程的z变换。
将差分方程转变为传递函数。
将a0作为标量增益系数进行分解。
估计频率响应。
对频率响应进行直接评估。
10.18 二阶前馈滤波器
二阶前馈滤波器的分析过程与你到目前为止看到的一阶滤波器很相似,但我们要处理的数学问题更多一些。二阶前馈滤波器的拓扑结构如图10.20所示。
10.18.1 第1步和第2步:对差分方程进行z变换并将其转化为传递函数。
我们可以合并步骤以节省时间。可以从图10.20a和b中分别提取样本中的差分方程,或进行z变换,如下所示。
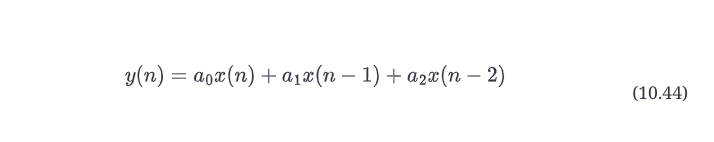
z变换可以通过检查,使用第10.9节的规则,然后我们需要把它变成Y(z)/X(z)的形式,用于传递函数,如公式10.45所示。

10.18.2 第3步:将a0作为标量增益系数进行分解
我们需要做一些替换来得到我们习惯的方程式10.46的形式。请注意,我们将多项式的前导值(z0项)强制为1.0--这样我们就可以在下一步对多项式进行因式分解以找到其根。
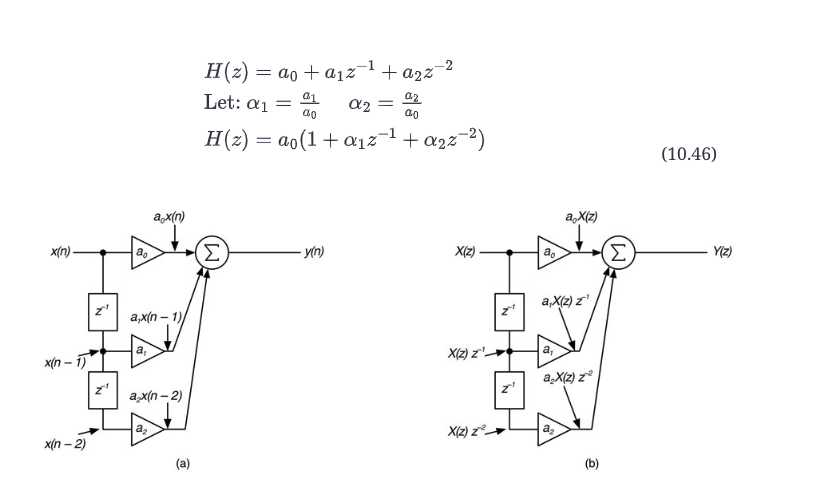
10.18.2 第3步:将a0作为标量增益系数进行分解 我们需要做一些替换来得到我们习惯的方程式10.46的形式。
10.18.3 第四步:估计频率响应
首先,这是一个纯前馈滤波器,所以我们知道只有非三阶零点,没有极点需要处理。由于Z-2项的存在,这个传递函数是一个二阶函数。事实上,这是一个二次方程。为了找到极点或零点,你需要首先对这个方程进行分解并找到根。问题是,这是一个复数方程,根可能是实数、虚数或两者的组合。我们得到的数学突破是,我们的系数α1和α2是实数。唯一的办法是,如果零点的位置是彼此的复共轭,那就可以解决这个问题。当你把复数共轭相乘时,虚数部分就会消失。因此,通过一点代数,你可以得出公式10.47所示的推论。

这种分析的结果是两个零点,Z1和Z2位于z平面上的复数共轭位置。图10.21a显示了一对任意共轭的零点在z平面上的分布。你可以看到它们是如何以相同的半径彼此成互补角的。记住,z平面上的任何任意点都位于RejΘ,圆的外缘对于R=1和Θ在-π和+π之间(或0到2π)进行评估。
但是,在RejΘ和Re-jΘ的一对复共轭零点与系数α1和α2的关系如何?答案是把所有的东西都乘出来,用欧拉方程,比较函数,如方程[10.48]和[10.49]中所示。


公式[10.48]和[10.49]显示了系数α1和α2如何在RejΘ和Re-jΘ的位置创建零点。你再一次看到,系数就是滤波器:它们决定了零点的位置,而这些决定了滤波器的频率和相位响应。为了演示如何使用图形解释和直接计算方法来估计频率响应,我们需要一些系数来测试。用下面的方法。
a0 = 1.0
a1 = -1.27
a2 = 0.81
现在,从公式10.49中计算出零点的位置;由于a0 = 1.0,那么α1 = -1.27,α2 = 0.81。从α2开始,然后求解方程10.50中的α1。图10.21b列出了零点。
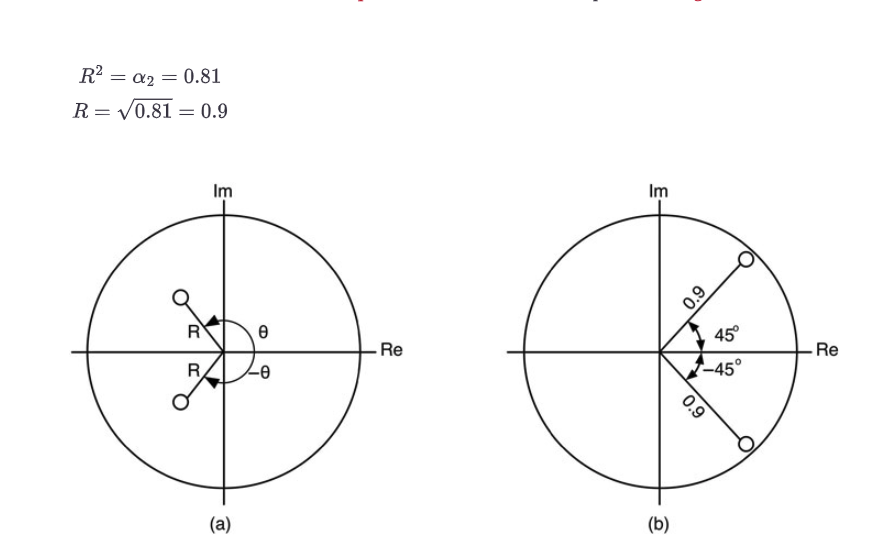
图10.21:(a)在半径R和角度Θ的z平面上绘制的一对任意共轭零点。(b) 在半径=0.9和角度为±45度时的一对互补零点。
然后
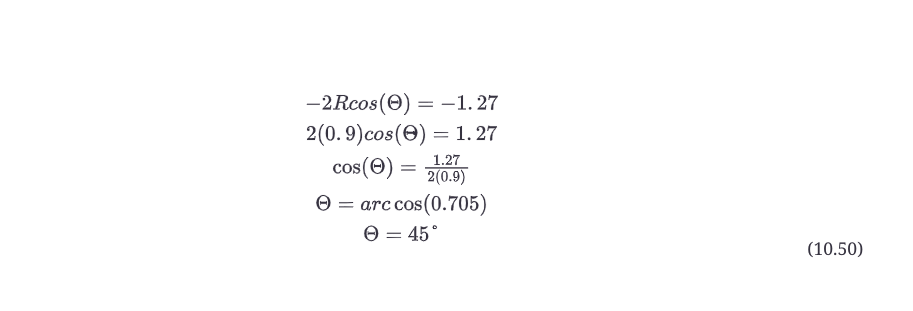
评估复数对的频率响应与之前类似,但多了一个步骤。当用一个以上的零点来估计频率响应时,要做以下工作。
在单位圆的外缘找到每个评估频率。
从圆上的点到每个零点画一条线,测量这些向量的长度。对每个评价频率都这样做。
对于每个评估频率,转移函数的大小是两个向量与每个零点对的乘积。
在数学上,这最后一条规则看起来像方程式10.51。
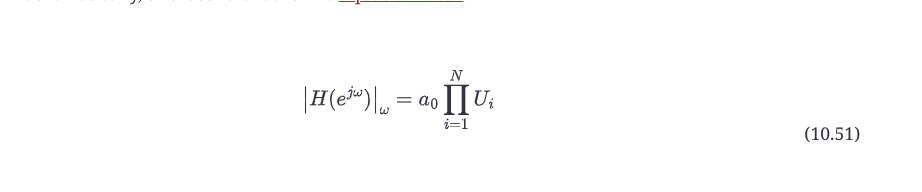
其中
N = 滤波器等级
Ui = 单位圆上的点ω到第i极的几何距离
按照图10.22-10.25的进度,从直流(0 Hz)开始,通过四个评估频率。在每个图中,Z平面图显示在(a)中,一条垂直线被放置在相应的
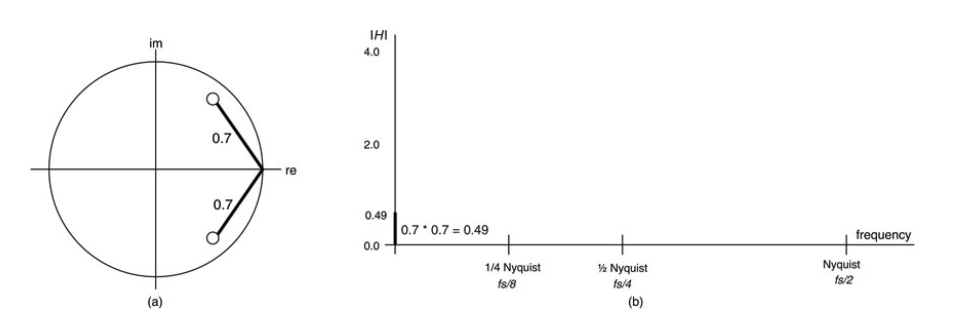
图10.22:0赫兹(直流)的幅度响应是两个向量画到每个零点的乘积,即0.49;这里我们计算了0赫兹的第一条幅度线;(a)Z平面图,(b)直流的幅度响应绘制为垂直线。
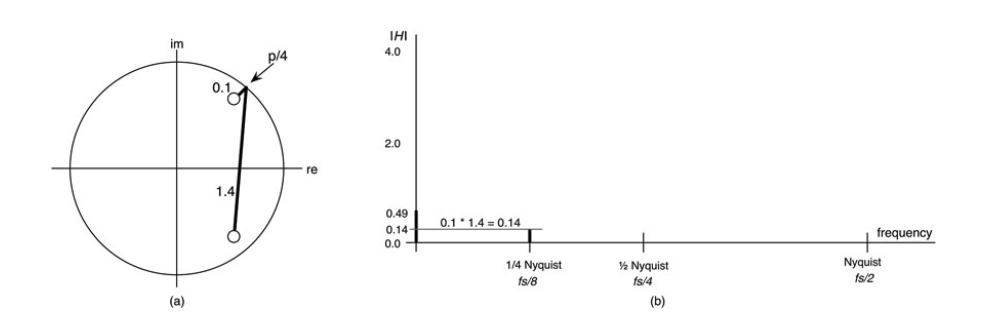
图10.23:在¼奈奎斯特,两个向量相乘为0.14;(a)Z平面图,(b)在¼奈奎斯特的幅度响应绘制为一条垂直线。
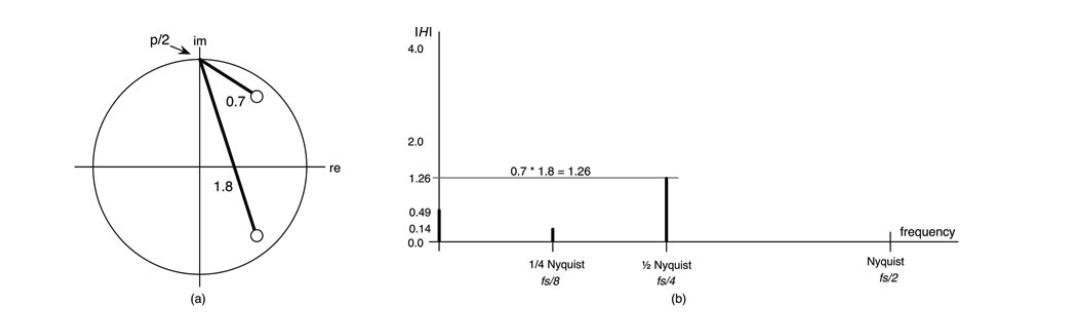
图10.24:在1/2奈奎斯特,响应达到1.26,因为矢量又开始延伸;(a)Z平面图,(b)在1/2奈奎斯特的幅值响应图为垂直线。
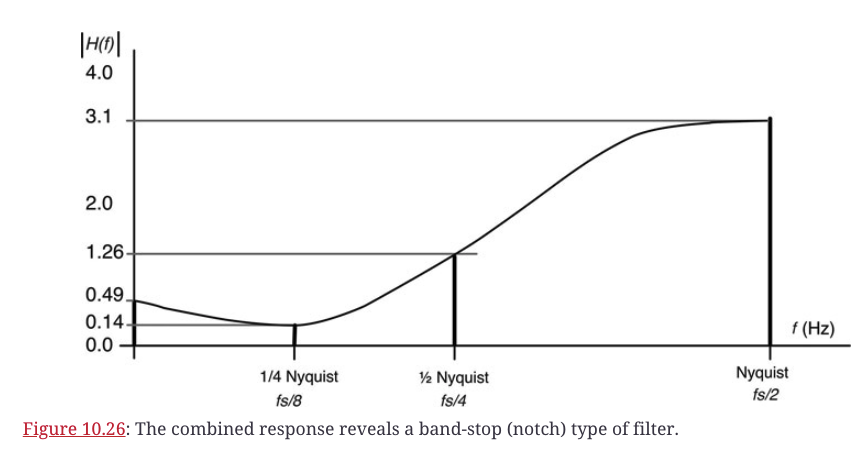
(b)中的响应图中的位置。最后,把所有的东西都放在一个图中,勾勒出图10.26中的幅度响应。分析显示了一个陷波滤波器。最小振幅发生在零频率,那里的矢量乘积最低--这是在正频率弧上求值时得到的最小矢量。
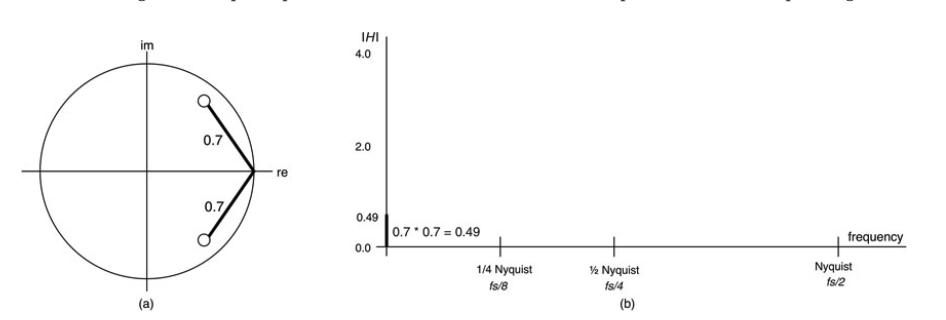
图10.22:0赫兹(直流)的幅度响应是两个向量画到每个零点的乘积,即0.49;这里我们计算了0赫兹的第一条幅度线;(a)Z平面图,(b)直流的幅度响应绘制为垂直线。
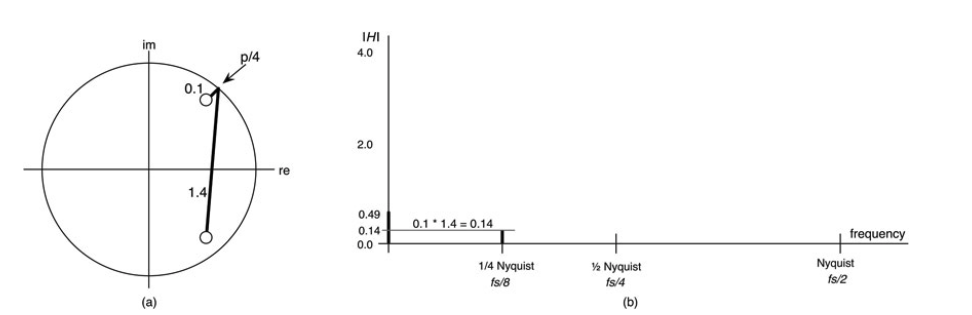
图10.23:在¼奈奎斯特,两个向量相乘为0.14;(a)Z平面图,(b)在¼奈奎斯特的幅度响应绘制为一条垂直线。
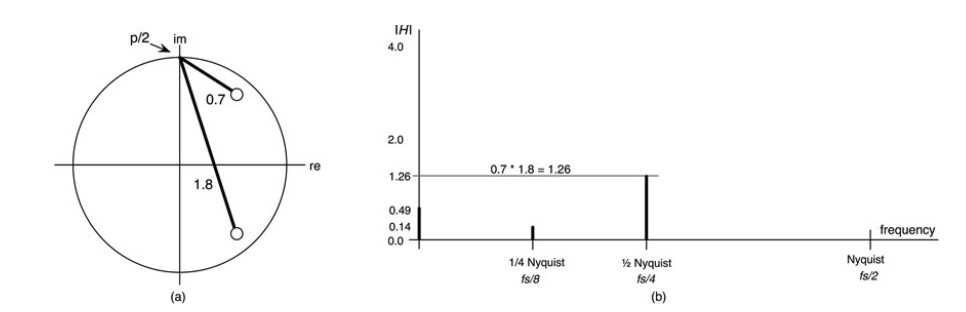
图10.24:在1/2奈奎斯特,响应达到1.26,因为矢量又开始延伸;(a)Z平面图,(b)在1/2奈奎斯特的幅值响应图为垂直线。
(b)中的响应图中的位置。最后,把所有的东西都放在一个图中,勾勒出图10.26中的幅度响应。分析显示了一个陷波滤波器。最小振幅发生在零频率,那里的矢量乘积最低--这是在正频率弧上求值时得到的最小矢量。
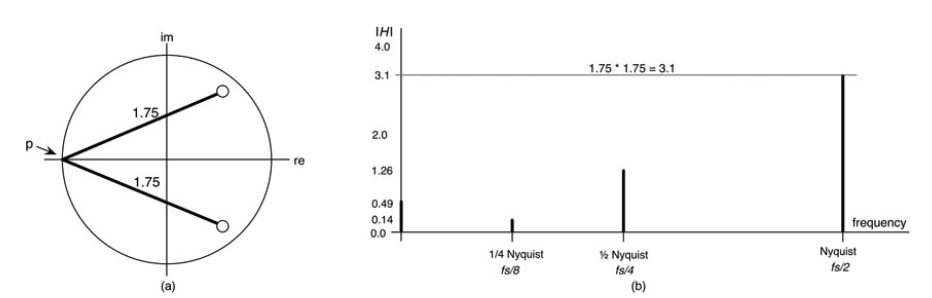
图10.25:在奈奎斯特,当矢量延伸到可能的最长长度时,响应达到最大值3.1;(a)Z平面图和(b)奈奎斯特的幅值响应绘制为垂直线。
10.18.4 第五步:直接评估
现在我们可以用之前的方法来评估滤波器:用欧拉方程来分离传递函数的实部和虚部,然后找出幅值和相位分量来生成一个图。
在以下频率下进行评估。
直流:0
奈奎斯特:π
1/2 奈奎斯特:π/2
¼ 奈奎斯特:π/4
首先以一种形式获得传递函数,以用于所有评估频率。
现在对四个频率中的每一个进行评估,从方程10.53的直流开始。我们现在省略了一些中间的数学步骤;确保你了解如何从一行到另一行,如果需要的话,可以用手算出来。
10.18.5 直流 (0 Hz)


准确的量级是0.54,这与我们用Z面图形法估计的0.49的值相当接近。
10.18.6 奈奎斯特(π)

准确的量级是3.08,这与我们用Z面图形法估计的3.1的值接近。
10.18.7 ½ Nyquist (π/2)

准确的量级是1.28,这与我们用Z面图形法估计的1.26的值很接近。
10.18.8 ¼ 奈奎斯特(π/4)

准确的量级是0.136,这与我们用Z面图形法估计的0.14的值相当接近。
10.18.9 脉冲响应的z变换
这个二阶前馈滤波器实际上很容易考察其脉冲响应。对于一个脉冲刺激,脉冲响应h(n)是:h(n) = {1.0, -1.27, 0.81}。如公式10.57所示,取脉冲响应的z变换很容易。

这正是我们所期望的。这应该有助于你理解关于纯前馈滤波器的另外两个非常重要的细节。
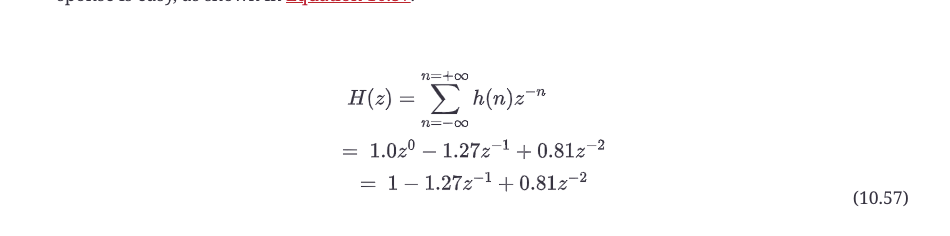
这正是我们所期望的。这应该有助于你理解关于纯前馈滤波器的另外两个非常重要的细节。
在一个纯前馈滤波器中。
系数{a0, a1, a2, ...}是脉冲响应,h(n)。
传递函数是系数的z变换。
图10.27a显示了频率响应,图10.27b显示了这个例子的相位响应。我们的估计和直接计算都与实际滤波器的行为非常吻合。
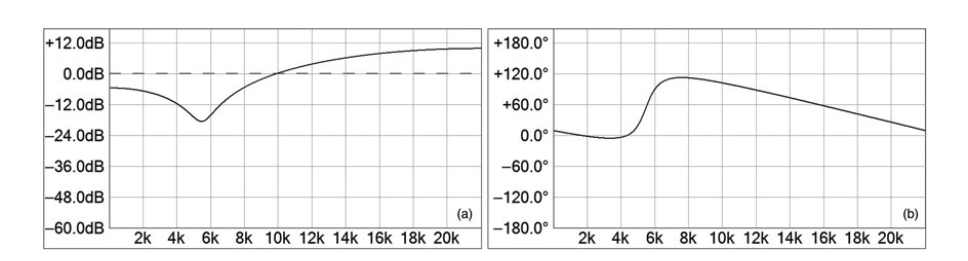
图10.27:二阶前馈滤波器的实测响应,fs = 44.1 kHz,a0 = 1.0,a1 = -1.27,a2 = 0.81,(a)频率响应和(b)相位响应。
10.19 二阶反馈滤波器
二阶反馈滤波器的分析从框图和差分方程开始。图10.28a显示了二阶反馈滤波器的拓扑结构。差分方程如下。
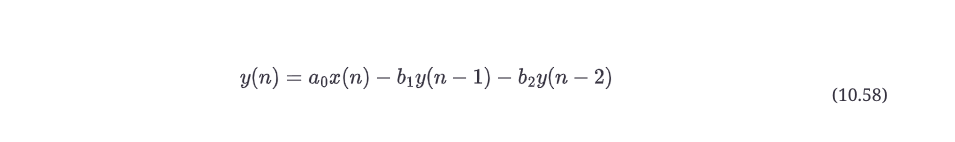
10.19.1 第1步、第2步和第3步:对差分方程进行z变换以得到传递函数,然后将a0作为标量增益系数进行分解。
我们将继续结合步骤。再一次,z变换可以通过检查、使用第10.9节中的规则或者通过推动X(z)通过滤波器来获得,如图10.28b所示。然后我们需要把它变成Y(z)/X(z)的形式,用于公式10.59的传递函数。

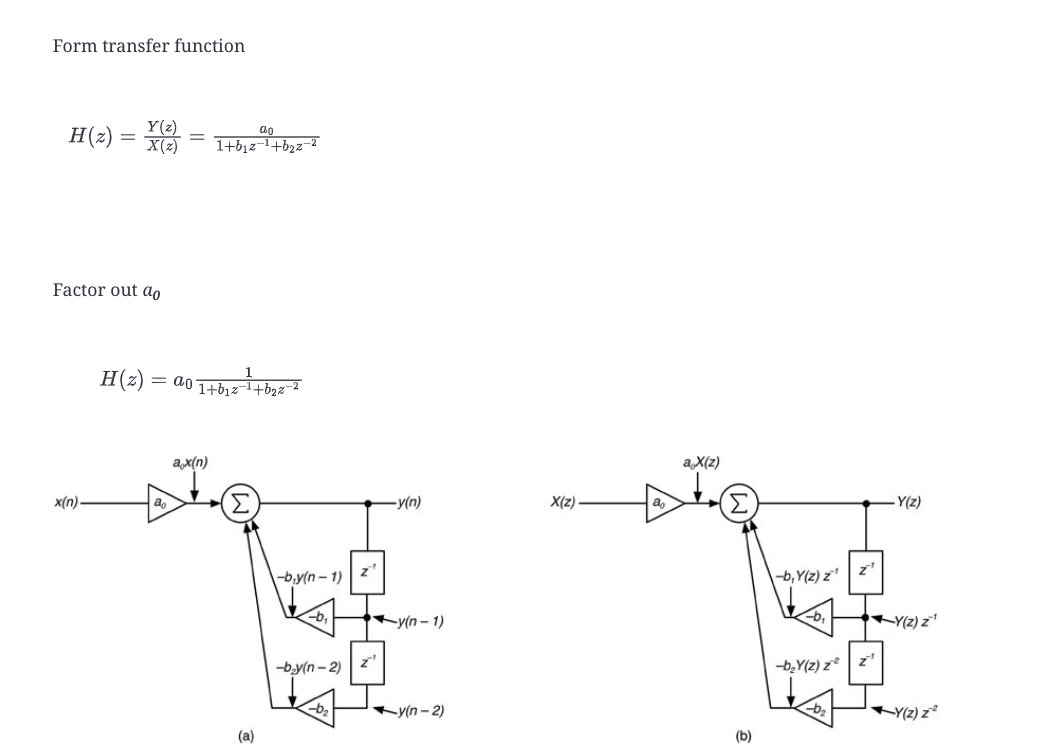
图10.28:二阶反馈结构,(a)离散样本x(n)和y(n)作为输入和输出,(b)整个信号X(z)和Y(z)作为输入和输出。
10.19.2 第四步:估计频率响应
现在你终于可以明白为什么反馈滤波器框图中的所有b系数都被否定了。这使得公式10.59中最终传递函数的二次分母与前馈传递函数的分子具有相同的多项式形式,匹配。方程10.45。因此,我们可以用同样的逻辑来寻找滤波器的极点:因为系数b1和b2是实值,所以极点必须是彼此的复共轭,如方程10.60所得出的。


这导致了两个极点,P1和P2,位于Z平面上的复数共轭位置。图10.29a显示了一对任意共轭的极点在Z平面上的分布。你可以看到它们是如何
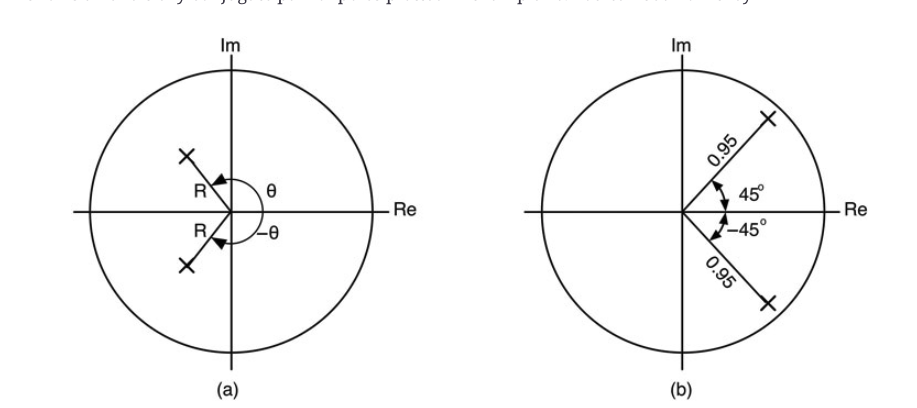
图10.29:(a)在半径R和角度Θ的Z平面上绘制的一对任意共轭极点。(b) 在半径=0.95和角度±45度的一对互补的零点。
是在半径相同的情况下,相互之间有互补的角度。为了演示,我们需要一些系数来测试。用下面的方法。
a0 = 1.0
a1 = -1.27
a2 = 0.81
现在,根据公式10.61计算出极点的位置。图10.29b显示了复数共轭的一对极点在Z平面上的角度为±45度,半径为0.95。

评估复数对的频率响应与之前类似,但多了一个步骤。当用一个以上的极点来估计频率响应时,请执行以下步骤。
在单位圆的外缘找到每个评估频率。
从圆上的点到每个极点画一条线,测量这些向量的长度。对每个评价频率都这样做。
对于每个评估频率,传递函数的大小是到每个极点对的两个向量的反长度的乘积。
在数学上,这最后一条规则看起来像方程式10.62。
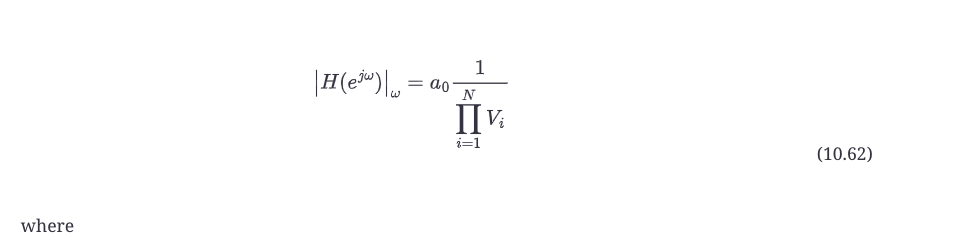
其中
N = 滤波器的阶数
Vi = 从单位圆上的点(ω)到第i极的几何长度
因此,这个过程与处理零点的过程相同,只是你要取到极点的长度的倒数。
对于前馈滤波器
频率离零点越近,收到的衰减就越大。
如果零点在单位圆上,幅度就会在这一点上归于零。
对于反馈滤波器
评估频率越接近极点,它收到的增益就越多。
如果极点在单位圆上,理论上幅度会到无限大,而且会产生一个振荡器,在极点频率上永远响个不停。
在一个数字滤波器中。
零点可以位于Z平面的任何地方--在单位圆内,在单位圆上,或在单位圆外,因为滤波器总是稳定的,它的输出不能低于0.0。
极点必须位于单位圆内。
如果一个极点在单位圆上,它就会产生一个振荡器。
如果一个极点在单位圆之外,当输出达到无穷大时,滤波器就会炸毁。
我们在第2章的练习中炸毁了一阶反馈滤波器,所有的反馈滤波器在其极点超出单位圆时都容易炸毁。现在我们可以继续对标准的四个评估频率进行估计。这一次,我们将把原始幅度值转换为分贝。这样做的原因是,如果我们不使用dB,将会有一个非常广泛的数值范围,很难勾勒出来。按照图10.30-10.33的评估顺序。
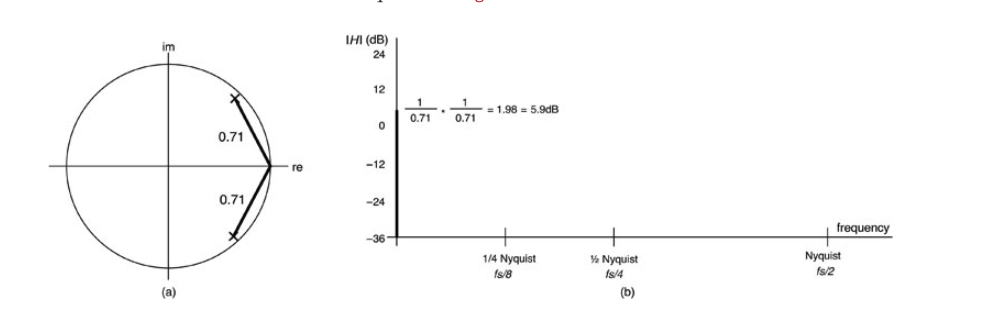
图10.30:0赫兹(DC)处的幅度响应是两个向量的逆向画在每个零点上的乘积,或(1/0.71)(1/0.71)=5.9dB;(a)Z平面图,(b)DC处的幅度响应绘制成垂直线。
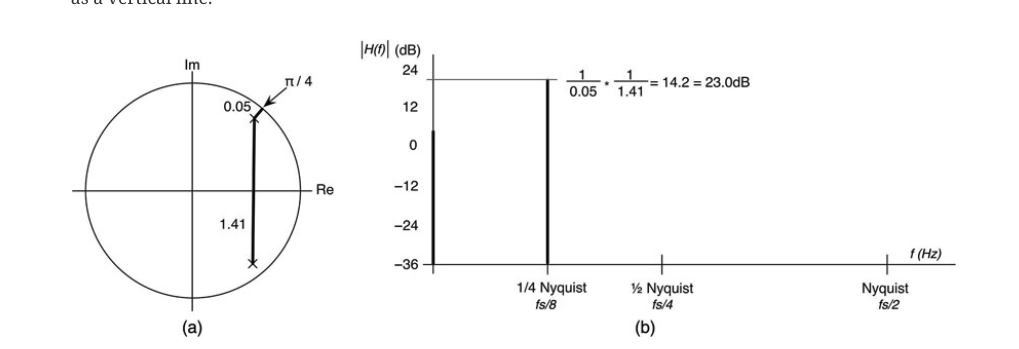
图10.31:π/4处的幅度响应高达+23dB,因为0.05的倒数是一个很大的数字;(a)Z平面图,(b)π/4处的幅度响应绘制为一条垂直线。
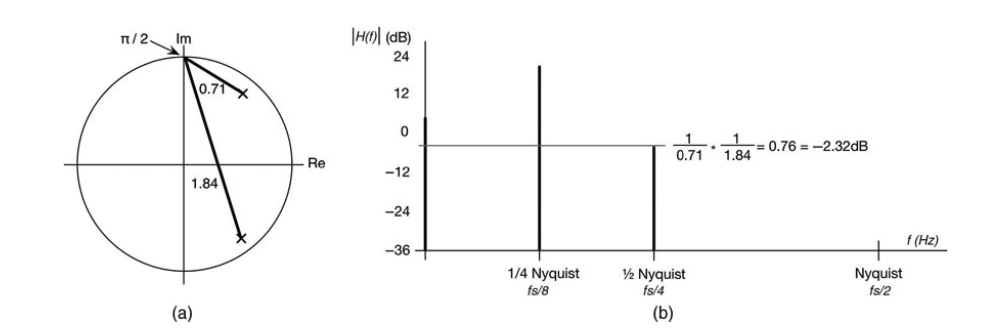
图10.32:π/2处的幅度响应为-2.98dB;(a)Z平面图,(b)π处的幅度响应绘制为垂直线。
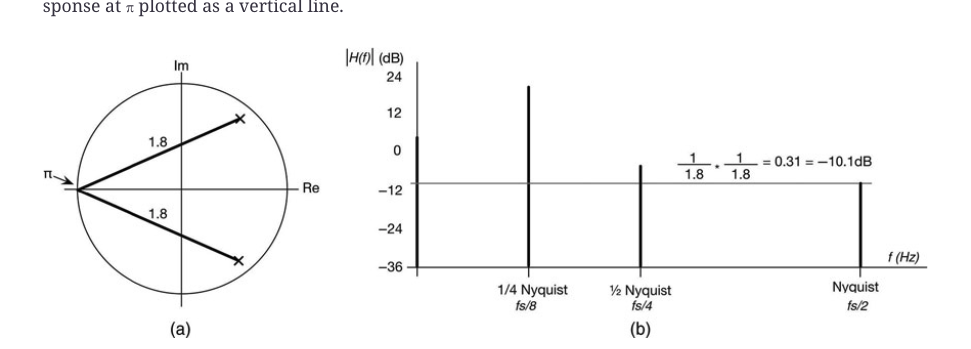
图10.33:π处的幅度响应为-10.1dB;(a)Z平面图,(b)π处的幅度响应绘制为垂直线。
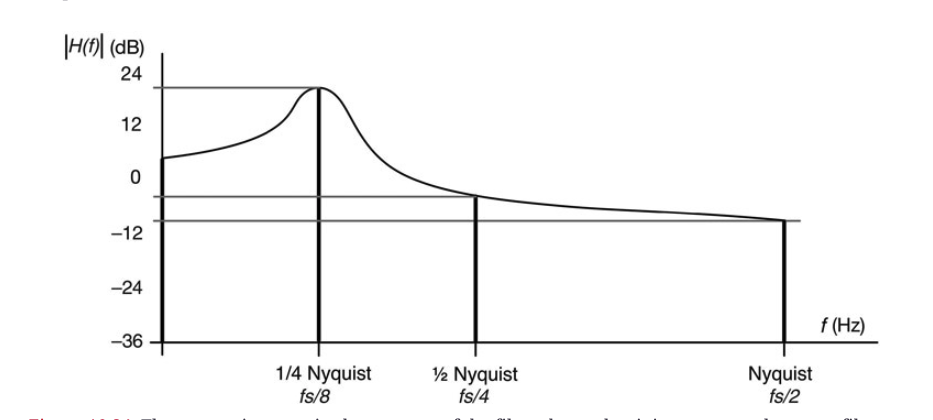
图10.34:滤波器的综合幅度响应显示它是一个谐振式低通滤波器;谐振峰出现在极点频率π/4。
在每个图中,(a)中显示的是Z平面图,(b)中在响应图的相应位置放了一条垂直线。最后,把它放在一起,形成图10.34的频率响应图。
10.19.3 第五步:直接评估
现在我们可以用之前的方法来评估滤波器:用欧拉方程来分离传递函数的实部和虚部,然后找出每个评估频率的幅值和相位分量。
在以下频率下进行评估。
直流:0
奈奎斯特:π
1/2 奈奎斯特:π/2
¼ 奈奎斯特:π/4
首先获得传递函数的形式,以用于公式10.63中所示的所有评估频率。

现在,从直流开始,对我们四个频率中的每一个进行评估。
10.19.4 DC (0 Hz)
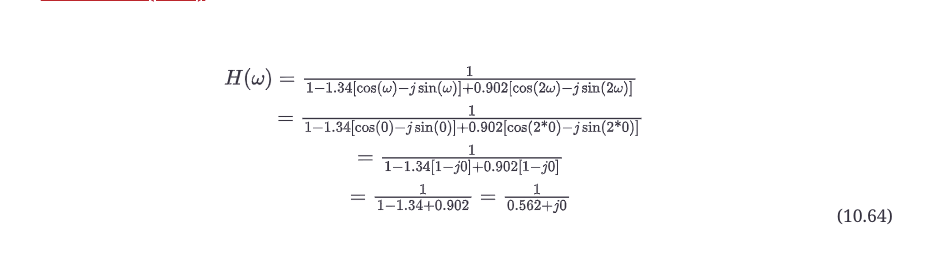
寻找幅度和相位需要检查分子和分母,就像二阶前馈情况一样。

记住,对于分数的大小,你需要分别取分子和分母的大小;而对于相位响应,最终的Arg(H)是Arg(分子)和Arg(分母)之差。直接评估的结果是5.00分贝,并显示我们的草图评估有点偏差,是5.9分贝。
10.19.5 练习
自己完成其余的直接评估计算。答案在表10.4中。
图10.35a和b显示了这个二阶反馈滤波器的测量频率和相位响应。
10.20 一阶极点/零点滤波器。搁置滤波器
一阶磁极/零点滤波器由同一算法中的一阶磁极和一阶零点组成。图10.36a中的拓扑结构是前馈和反馈部件的组合,因为该结构包含了两种路径。音频工程师通常将其称为搁置滤波器,而DSP工程师通常将其称为极点/零点(p/z)滤波器。
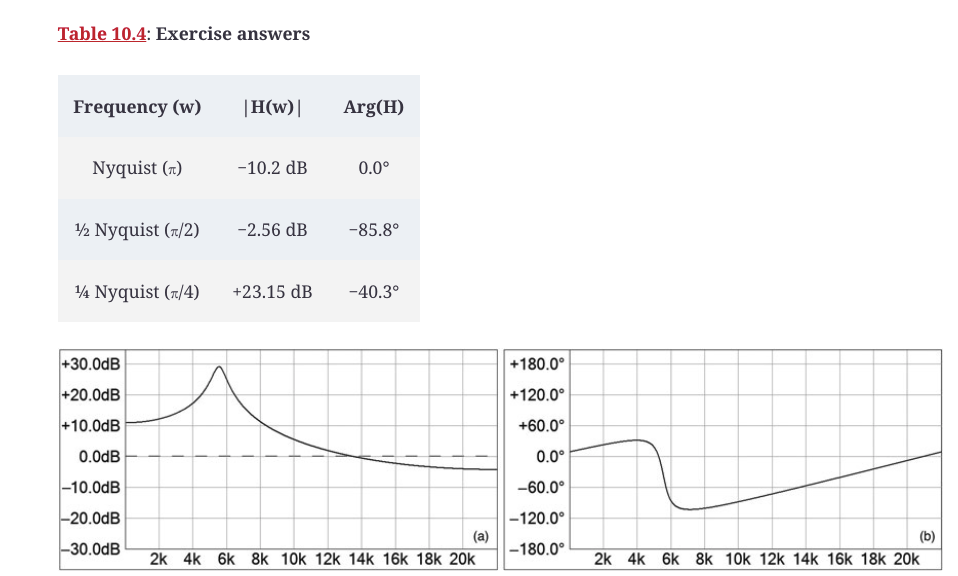
图10.35:二阶反馈滤波器的实测响应,fs = 44.1 kHz,a0 = 1.0,b1 = -1.34,b2 = 0.902,(a)频率响应和(b)相位响应。
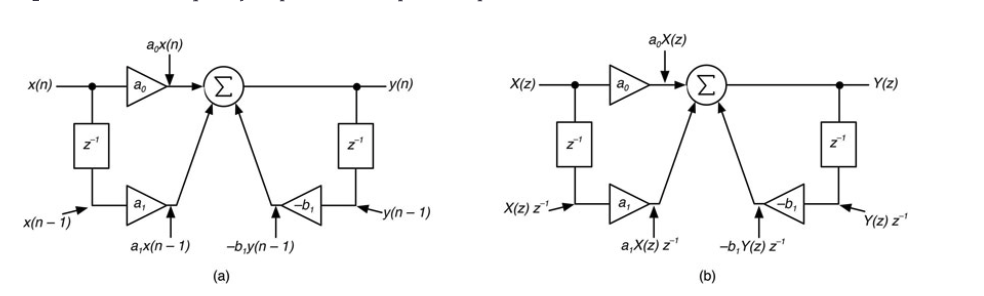
图10.36:一阶极点/零点滤波器,(a) 离散样本x(n)和y(n)作为输入和输出。(b) 整个信号X(z)和Y(z)作为输入和输出。
差分方程为:
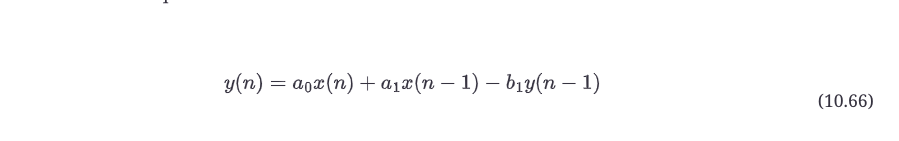
10.20.1 第1步、第2步和第3步:对差分方程进行z变换以获得传递函数,然后将a0作为标量增益系数进行分解。
再一次,Z变换可以通过检查,使用第10.9节中的规则,或者从推动X(z)通过滤波器得到,如图10.36b所示,然后我们需要把它变成Y(z)/X(z)的形式,用于公式10.67的传递函数。

10.20.2 第四步:估计频率响应
这个传递函数有一个极点和一个零点,都是一阶的。与其他一阶情况一样,我们可以通过检查方程10.68中的传递函数找到极点和零点。
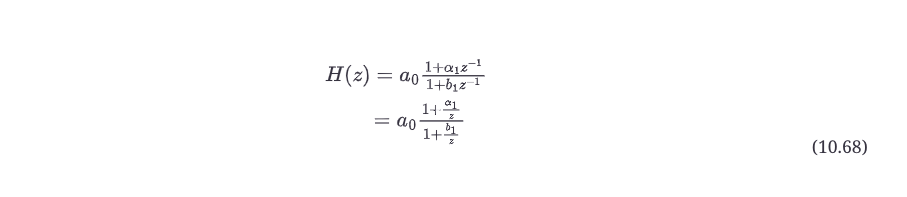
在分子中,你可以看到,如果z=-α1,分子将归零,转移函数将归零。在分母中,你可以看到,如果z=-b1,分母将归零,转移函数将归于无穷大。因此我们在z=-α1处有一个零点,在z=-b1处有一个极点。
对于这个例子,使用以下的系数值。
a0 = 1.0
a1 = -0.92
b1 = -0.71
然后,α1=-0.92;所以我们现在有一个零点在z=-α1=0.92+j0,一个极点在z=-b1=0.71+j0。这对极点/零点被绘制在图10.37中。
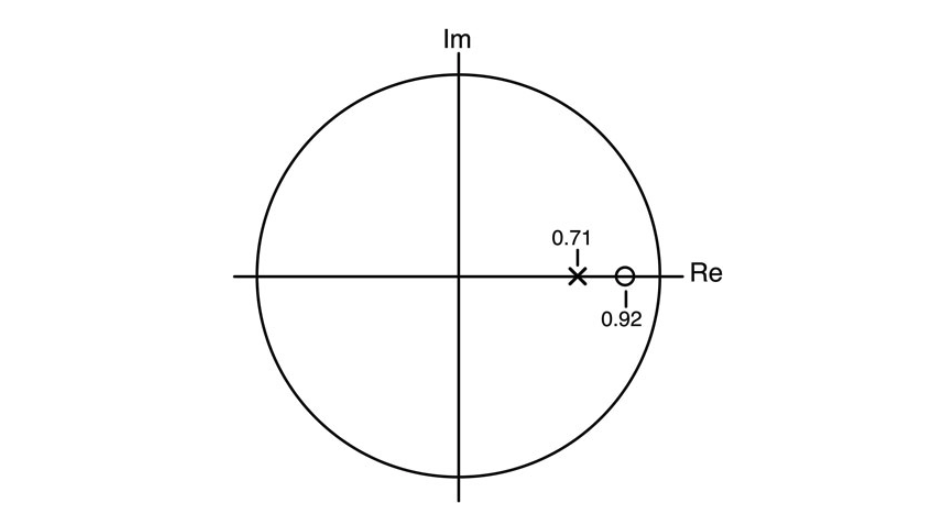
图10.37:极点和零点都是纯实数,绘制在Z平面的实轴上。
当你有混合极点和零点时,评估频率响应与之前一样,但你必须实现两个幅度的步骤。
将每个评估频率定位在单位圆的外缘。
从圆上的点到每个零点画一条线,测量这些向量的长度。对每个评估频率都这样做。
从圆上的点到每个极点画一条线,测量这些向量的长度。对每个评估频率都这样做。
将所有的零点幅度相乘。
将所有的反极点幅度相乘。
用零点幅度除以极点幅度,得到该频率下的最终结果。
在数学上,这最后一条规则看起来像方程式10.69。
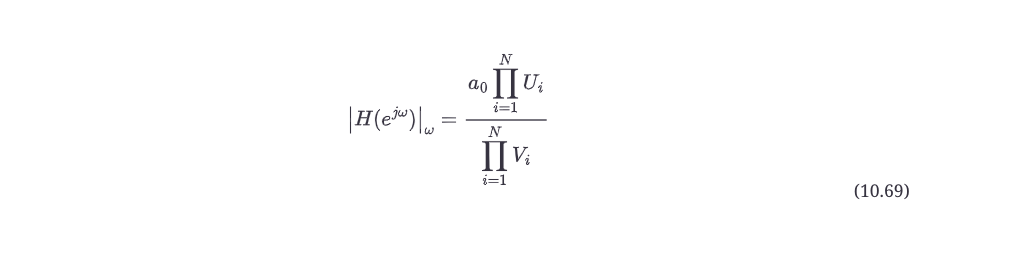
其中
N = 滤波器的阶数
Ui = 从单位圆上的点(ω)到第i个零点的几何长度
Vi = 从单位圆上的点(ω)到第1个极点的几何长度
方程10.69是最终的、通用的幅度响应方程,用于对任何数量的极点和零点的Z平面上的极点/零点图进行几何解释。为了完整起见,下面是用几何方法计算数字滤波器的相位响应的方程式。
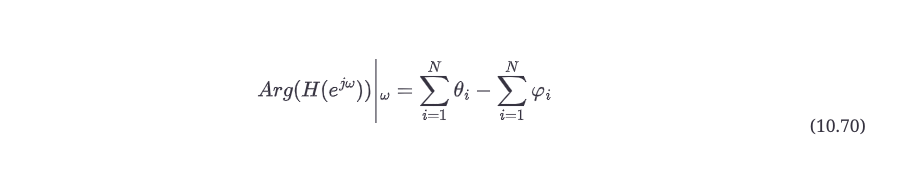
其中
N = 滤波器的阶数
θi = 第1个零点与矢量Ui之间的角度
φi = 第1个极点与向量Vi之间的角度
方程10.69和10.70共同完成了DSP的极点/零点解释理论,用于估计任何有任何数量极点和零点的滤波器的频率和相位响应。那么,让我们对这个滤波器进行分析。其中一个有趣的地方是,通过数学运算,你可以看到极点和零点之间的拉锯战。按照图10.38-10.41的分析顺序,在每个图中,Z面图显示在(a)中,垂直线放在(b)中响应图的相应位置。例如,在图10.38a中,你可以看到零点获胜,响应下降了近12分贝。从几何上看,你可以看到这是因为零点离评估点更近,所以它对结果的影响更大。在任何一个滤波器中,分子和分母最终都会打架--有些情况下,分子会赢,有些情况下,分母会赢,有时还会打成平手,在这种情况下,滤波器的幅度在该评估频率上是统一增益。图10.42中显示了综合图;注意Y轴已经被放大,以便于观察架子的情况。
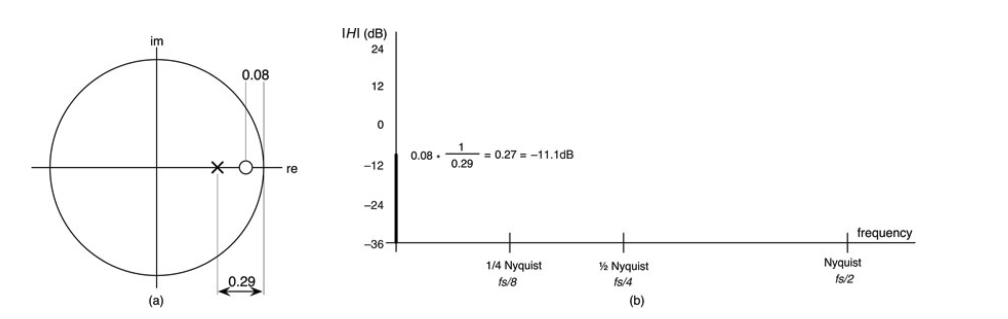
图10.38:直流处的幅值响应为-11.1dB,因为零点赢得了这场战斗;(a)Z平面图,(b)直流处的幅值响应绘制为一条垂直线。
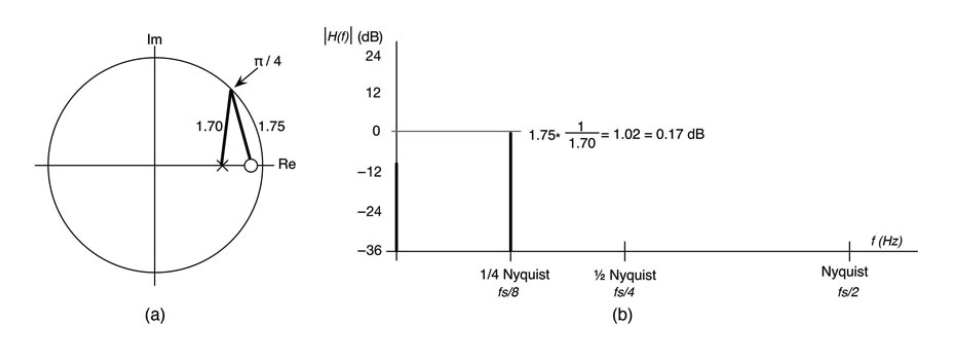
图10.39:π/4处的幅度响应几乎是统一的增益,因为极点和零点距离几乎相同。拔河比赛在这里以0.17dB的增益僵持结束;(a)Z平面图,(b)π/4处的幅度响应绘制成一条垂直线。
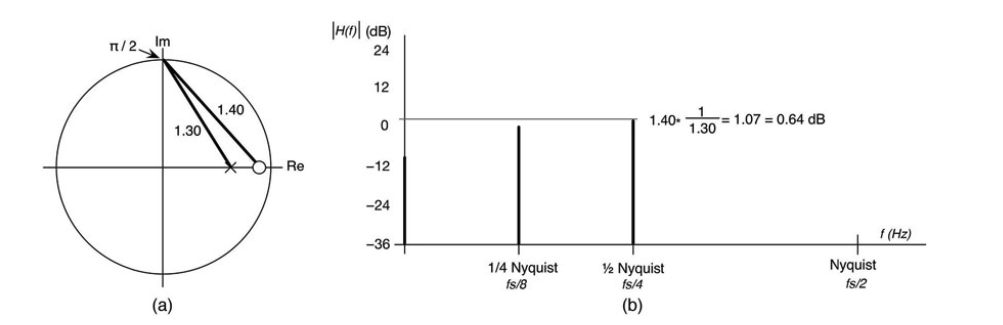
图10.40:当极点稍稍靠近评估频率时,π/2处的幅度响应提高了一点,达到+0.64dB;(a)Z平面图,(b)π/2处的幅度响应绘制成一条垂直线。
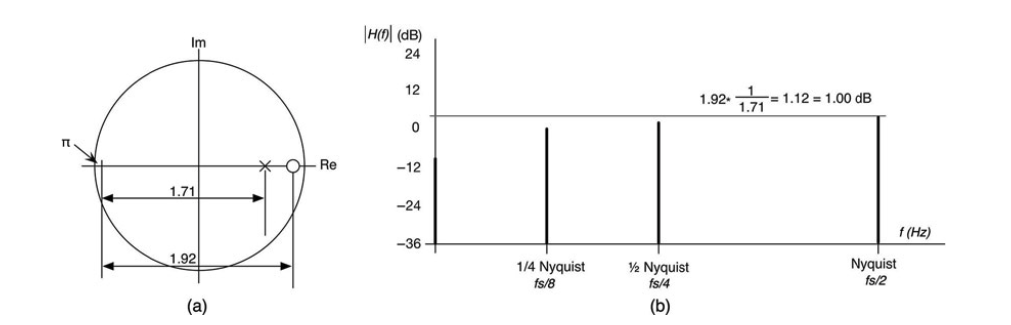
图10.41:在π处,极点/零点比率偏向于极点,响应提高到1.0dB;注意这是极点明显占优势的频率,但只是勉强的;(a)Z平面图,(b)π处的幅度响应绘制为垂直线。
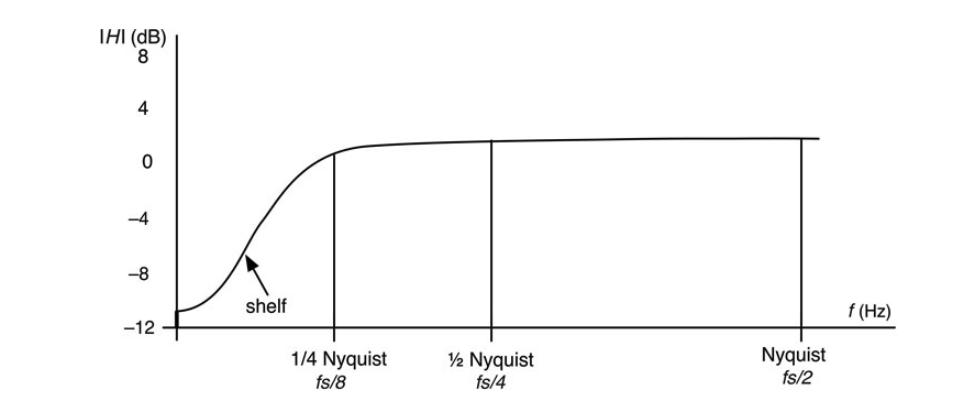
图10.42:复合频率响应图显示了一个-12dB的低搁置滤波器响应--一个在音频中有用的滤波器。
10.20.3 第五步:直接评估
现在我们可以用之前的方法来评估滤波器:用欧拉方程来分离传递函数的实部和虚部,然后找出每个评估频率的幅值和相位分量。
在以下频率下进行评估。
直流:0
奈奎斯特:π
1/2 奈奎斯特:π/2
¼ 奈奎斯特:π/4
首先以一种形式获得传递函数,以用于所有评估频率,如公式10.71所示。

10.20.4 DC (0 Hz)

10.20.4.1 Exercise
自己完成其余的直接评估计算。答案在表10.5中。
图10.43显示了这个搁架式滤波器的测量频率响应,图中有(a)线性频率(与我们这里的图吻合)和(b)对数频率轴,这与你最熟悉的搁架式滤波器的响应相似。
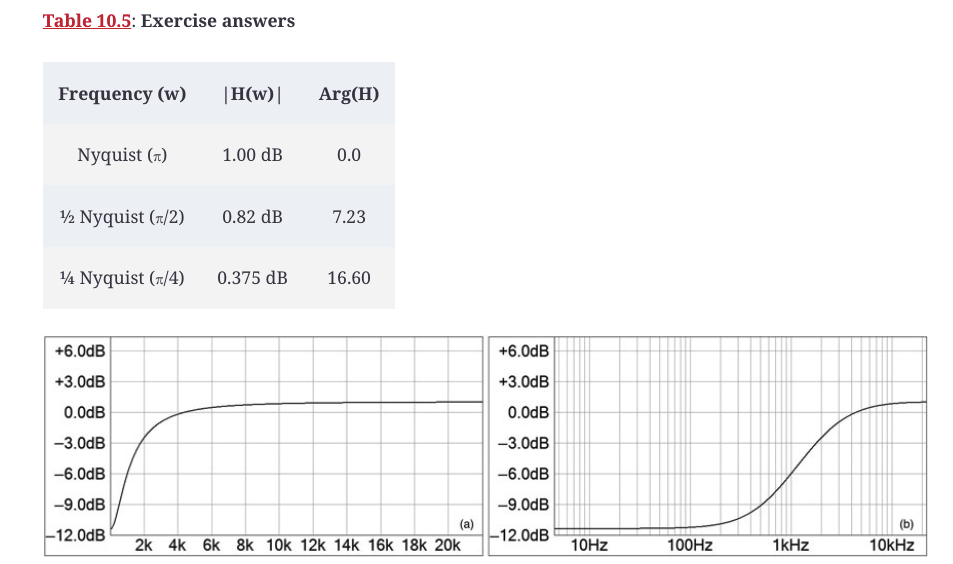
图10.43:我们的极点/零点搁置滤波器的测量(a)线性和(b)对数频率响应图,fs=44.1kHz。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!
· AI与.NET技术实操系列(二):开始使用ML.NET
· 单线程的Redis速度为什么快?