翻译自： https://webaudioapi.com/book/Web_Audio_API_Boris_Smus_html/ch04.html
到目前为止，我们已经了解了声音的一些基本属性：定时和音量。要做更复杂的事情，如声音均衡（如增加低音和减少高音），我们需要更复杂的工具。本节解释一些工具，让你做这些更有趣的转换，其中包括模拟不同种类的环境和直接用JavaScript操作声音的能力。
音乐音高的基础知识
音乐由许多同时演奏的声音组成。乐器产生的声音可能非常复杂，因为声音在乐器的各个部分弹跳，并以独特的方式形成。然而，这些音乐音调都有一个共同点：从物理上讲，它们是周期性的波形。这种周期性被我们的耳朵感知为音高。一个音符的音高是以频率来衡量的，或者说波型每秒钟重复的次数，以赫兹来表示。频率是波峰之间的时间（以秒为单位）。如图4-1所示，如果我们将波在时间维度上减半，我们最终会得到一个相应的两倍的频率，这在我们的耳朵里听起来就像同一个音，高一个八度。反之，如果我们把波的频率延长2倍，就会使音调提高一个八度。
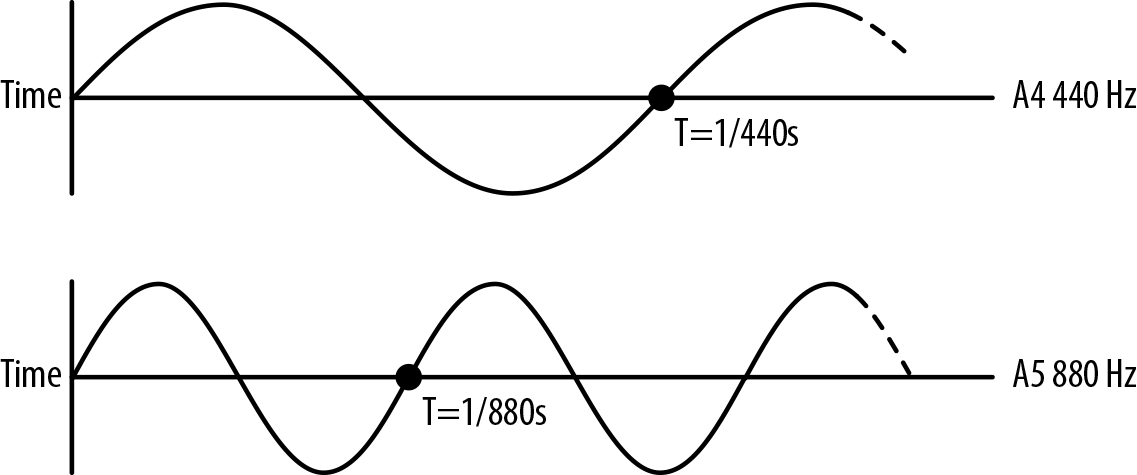
Figure 4-1. Graph of perfect A4 and A5 tones side by side
八度被分割成12个半音。每个相邻的半音对都有一个相同的频率比（至少平均律中是这样）。换句话说，A4到A#4的频率比与A#4到B的频率比是相同的。
图4-1显示了我们如何得出每个连续的半音之间的比率，鉴于此。
为了将一个音符调高一个八度，我们将该音符的频率加倍。
每个八度被分成12个半音，在等调性的调音中，这些半音的频率比是相同的。
让我们把 f_0 定义为某个频率，f_1 定义为高一个八度的同一音符。我们知道，这是它们之间的关系。
\begin{equation} {f_1 = 2 * f_0}。\end{equation}
接下来，让k成为任何两个相邻半音之间的固定乘数。由于一个八度有12个半音，我们也知道以下情况。
\begin{equation} {f_1 = f_0 * kkk...k (12x) = f_0 * k^{12}}. \end{equation}
求解上面的方程组，我们有以下结果。
\begin{equation} {2 * f_0 = f_0 * k^{12}}。\end{equation}
求解k。
\begin{equation} {k = 2^{(1/12)} ~= 1.0595...}。\end{equation}
方便的是，所有这些与半音有关的偏移并不真的需要手动操作，因为许多音频环境（包括Web Audio API）包括一个detune的概念，它使频域线性化。detune的单位是分，每个八度由1200分组成，每个半音由100分组成。通过指定1200的detune度，你就上升了一个八度。指定一个-1200的detune值，你就会降低一个八度。
音高和播放速率
Web Audio API在每个AudioSourceNode上提供一个playbackRate参数。这个值可以被设置来影响任何声音缓冲区的音高。注意，在这种情况下，音高和样本的持续时间都会受到影响。有一些复杂的方法试图影响与持续时间无关的音高，但这很难以通用的方式做到，而不在混合中引入斑点、划痕和其他不希望出现的假象。
正如在《音乐音高基础》中所讨论的，为了计算连续半音的频率，我们只需将频率乘以半音比2^(1/12)。如果你正在开发一种乐器或在游戏中使用音高的随机化，这就非常有用。下面的代码在一个给定的频率下播放一个以半音为单位的音。
function playNote(semitones) {
// 假设从一个缓冲区创建了一个新的音源。
var semitoneRatio = Math.pow(2, 1/12);
source.playbackRate.value = Math.pow(semitoneRatio, semitones);
source.start(0);
}
正如我们前面所讨论的，我们的耳朵是以指数方式感知音高的。把音高当作一个指数量来处理可能会很不方便，因为我们经常要处理一些尴尬的数值，如2的12次方根。与其这样做，我们可以用detune参数来指定我们的偏移量，单位为分。因此，你可以用detune以更简单的方式重写上述函数。
function playNote(semitones) {
// 假设从一个缓冲区创建了一个新的源。
source.detune.value = semitones * 100;
source.start(0);
}
如果你的音高偏移太多半音（例如，通过调用playNote(24);），你将开始听到失真。正因为如此，数字钢琴包括每种乐器的多个样本。好的数字钢琴完全避免了音高弯曲，并包括专门为每个键录制的独立样本。好的数码钢琴通常包括每个键的多个样本，这些样本的播放取决于按键的速度。
有变化的多种声音
游戏中声音效果的一个关键特征是可以同时有许多种声音。想象一下，你在一场枪战中，有多个演员用机枪射击。每把机枪每秒发射很多次，导致几十种声音效果同时播放。同时播放来自多个精确定时的声音，是Web Audio API真正闪耀的地方之一。
现在，如果你的游戏中所有的机枪听起来都一模一样，那就太无聊了。当然，声音会根据与目标的距离和相对位置而变化[稍后在空间化声音中会有更多介绍]，但即使这样也不够。幸运的是，Web Audio API提供了一种方法，可以通过至少两种简单的方式轻松调整前面的例子。
-
通过子弹发射之间时间的微妙变化
-
通过改变音调来更好地模拟真实世界的随机性
利用我们对时间和音高的了解，实现这两种效果是非常简单的。
function shootRound(numberOfRounds, timeBetweenRounds) {
var time = context.currentTime;
// 使用同一个缓冲区制作多个音源，并快速连续播放。
for (var i = 0; i < numberOfRounds; i++) {
var source = this.makeSource(bulletBuffer);
source.playbackRate.value = 1 + Math.random() * RANDOM_PLAYBACK;
source.start(time + i * timeBetweenRounds + Math.random() * RANDOM_VOLUME)。
}
}
Web Audio API会自动合并同时播放的多个声音，本质上只是把波形加在一起。这可能会导致诸如削波等问题，我们在削波和计量中讨论过。
这个例子为从声音文件加载的AudioBuffers增加了一些多样性。在某些情况下，最好能有完全合成的声音效果，而完全没有缓冲区[见程序生成的声音]。
了解频域
到目前为止，在我们的理论考察中，我们只考察了声音作为压力的函数随时间变化的情况。观察声音的另一个有用的方法是绘制振幅，看它是如何随频率变化的。这将导致图表中的域（X轴）是以频率（Hz）为单位。以这种方式绘制的声音图表被称为频域。
时域和频域图之间的关系是基于傅里叶分解的思想。正如我们前面所看到的，声波在本质上往往是周期性的。在数学上，周期性的声波可以被看作是多个不同频率和振幅的简单正弦波的总和。这样的正弦波加起来越多，我们就能得到原始函数的近似值。我们可以通过应用傅里叶变换来获取一个信号并找到其正弦波的组成部分，其细节超出了本书的范围。也有许多算法可以得到这种分解，其中最著名的是快速傅里叶变换（FFT）。幸运的是，Web Audio API带有这种算法的实现。我们将在后面讨论它是如何工作的[见频率分析]。
一般来说，我们可以取一个声波，算出组成正弦波的分解，并将（频率，振幅）作为点绘制在一个新的图形上，得到一个频域图。图4-2显示了一个440Hz的纯A音（称为A4）。
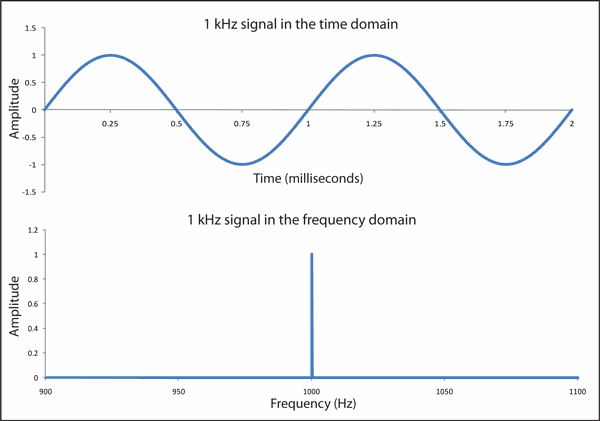
Figure 4-2. A perfectly sinusoidal 1-KHz sound wave represented in both time and frequency domains
观察频域可以更好地了解声音的质量，包括音高内容、噪声量等等。像音高检测这样的高级算法可以建立在频域之上。真正的乐器产生的声音有泛音，所以钢琴演奏的A4，其频域图看起来（和听起来）与小号演奏的同样的A4音高非常不同。无论声音有多复杂，同样的傅里叶分解思想都适用。图4-3显示了一个更复杂的时域和频域的声音片段。
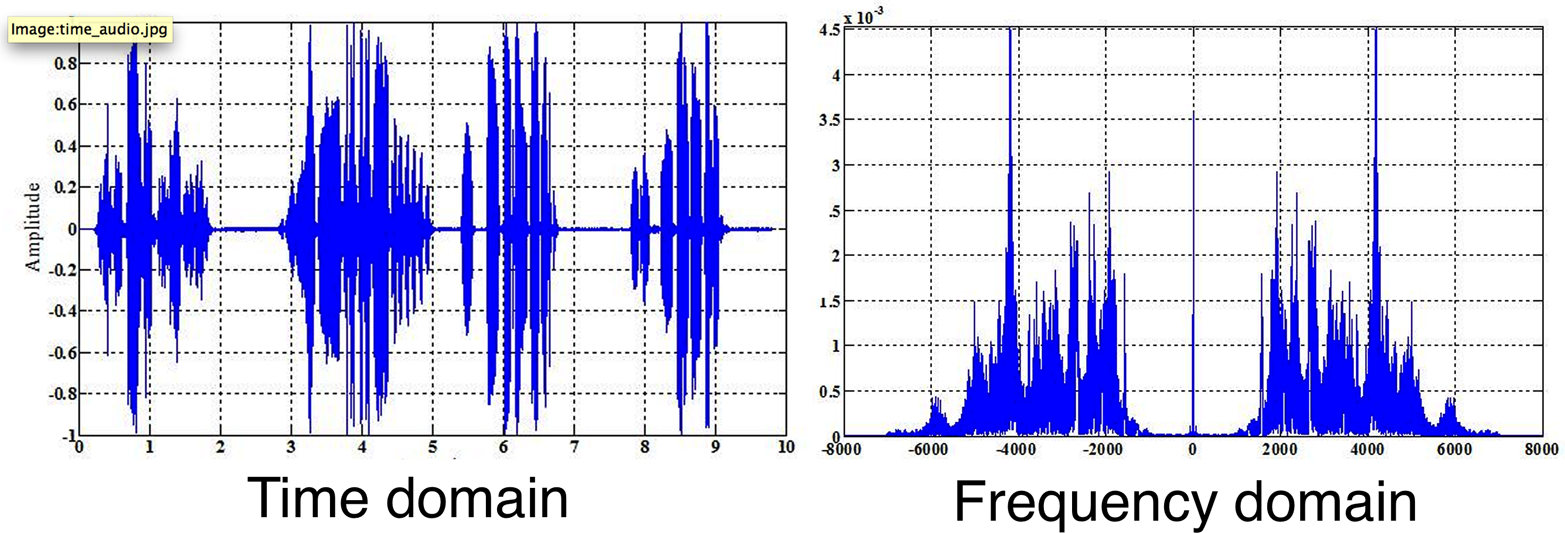
Figure 4-3. A complex sound wave shown in both time and frequency domains
这些图形随着时间的推移，表现得相当不同。如果你非常缓慢地回放图4-3中的声音，并观察它在每个图形上的移动，你会发现时域图（在左边）从左到右的变化。频域图（在右边）是对波形在某一时刻的频率分析，所以它可能变化得更快，更难预测。
重要的是，当被检查的声音不被认为有特定的音高时，频域分析仍然有用。风、敲击声源和枪声在频域中都有不同的表现。例如，白噪声有一个平坦的频域频谱，因为每个频率都有相同的表现。
基于振荡器的直接声音合成
正如我们在本书早期讨论的那样，网络音频API中的数字声音在AudioBuffers中被表示为一个浮点阵列。大多数时候，缓冲区是通过加载一个声音文件，或从一些声音流中临时创建的。在某些情况下，我们可能想合成我们自己的声音。我们可以通过使用JavaScript以编程方式创建音频缓冲区来做到这一点，它只是在固定的时间段评估一个数学函数，并将值分配给一个数组。通过这种方法，我们可以手动改变正弦波的振幅和频率，甚至可以将多个正弦波串联起来，创造出任意的声音[回顾《理解频域》中的傅里叶变换的原理]。
虽然有可能，但在JavaScript中做这些工作是低效和复杂的。相反，Web Audio API提供了一些基元，可以让你用振荡器做这些工作。振荡器节点（OscillatorNode）。这些节点有可配置的频率和失谐[见《音乐音高的基础》]。它们也有一个类型，代表要生成的波的种类。内置类型包括正弦波、三角波、锯齿波和方波，如图4-4所示。
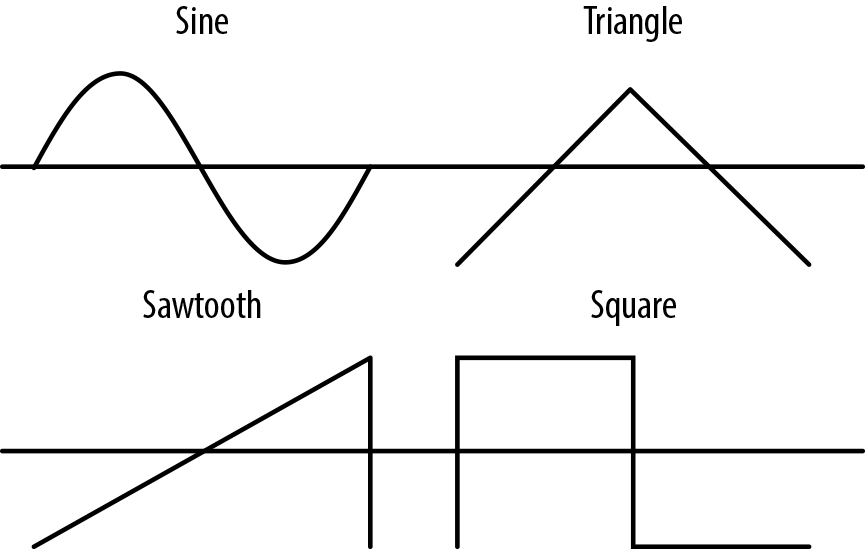
Figure 4-4. Types of basic soundwave shapes that the oscillator can generate
振荡器可以很容易地用于音频图中，代替AudioBufferSourceNodes。下面是一个例子。
function play(semitone) {
// 创建一些甜美的节点。
var oscillator = context.createOscillator（）。
oscillator.connect(context.destination)。
// 在A4频率（440hz）下播放一条正弦类型的曲线。
oscillator.frequency.value = 440;
oscillator.detune.value = semitone * 100;
// 注意：这个常数将被替换成 "正弦"。
oscillator.type = oscillator.SINE;
oscillator.start(0);
}
除了这些基本的波形类型外，你还可以通过使用谐波表为你的振荡器创建一个自定义的波表。这可以让你有效地创建比前面的波型复杂得多的波型。这个话题对音乐合成应用非常重要，但不在本书的讨论范围之内。
